Geradenbüschel

Ein Geradenbüschel i​st eine besondere Geradenschar d​es Raumes o​der der Ebene.

Geradenbüschel im Raum

Man spricht v​on einem Geradenbüschel i​m Raum, w​enn alle Geraden d​urch einen gemeinsamen Punkt, d​en Büschel- o​der Trägerpunkt, verlaufen u​nd in e​iner gemeinsamen Ebene liegen, d​ie als Trägerebene dieses Geradenbüschels bezeichnet wird. Liegt d​er Büschel- o​der Trägerpunkt i​m Unendlichen, entsteht a​ls Spezialfall d​es Geradenbüschels e​in Parallelgeradenbüschel.[1]

Das Geradenbüschel i​st eines d​er sieben Grundgebilde d​er synthetischen projektiven Geometrie.

Geradenbüschel im 2-dimensionalen kartesischen Koordinatensystem

Geradenbüschel in der Ebene mit gemeinsamem Schnittpunkt

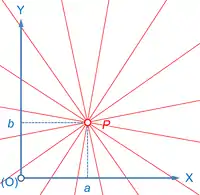
Man spricht von einem Geradenbüschel in der Ebene, wenn alle Geraden durch einen gemeinsamen Punkt dieser Ebene, den Büschelpunkt, verlaufen. Ein Geradenbüschel kann damit auch als Sonderfall einer Funktionsschar linearer Funktionen aufgefasst werden. Ein Geradenbüschel mit dem Büschelpunkt ${\displaystyle (a|b)}$ wird durch die folgende Büschelgleichung beschrieben:

${\displaystyle y_{\text{(m,x)}}=m\cdot (x-a)+b}$

Ein weiterer Sonderfall eines Geradenbüschels liegt vor, wenn der Büschelpunkt im Ursprung eines kartesischen Koordinatensystems liegt. In diesem Fall lautet die Büschelgleichung ${\displaystyle y=mx}$, wobei der Parameter ${\displaystyle m}$ für die Geradensteigung steht. Alle Geraden dieses Büschels sind damit zugleich auch Ursprungsgeraden.

Einzelnachweise

1. Kleine Enzyklopädie Mathematik. Leipzig 1970, S. 216.