Spielerfehlschluss
Der Spielerfehlschluss (englisch Gambler’s Fallacy) ist ein logischer Fehlschluss, dem die falsche Vorstellung zugrunde liegt, ein zufälliges Ereignis werde wahrscheinlicher, wenn es längere Zeit nicht eingetreten ist, oder unwahrscheinlicher, wenn es kürzlich/gehäuft eingetreten ist.
Dieser Denkfehler ist im Alltag auch bei der Beurteilung von solchen Wahrscheinlichkeiten verbreitet, die bereits sorgfältig analysiert sind. Viele Menschen verspielen seinetwegen Geld. Die Widerlegung dieser Überlegung lässt sich in dem Satz zusammenfassen: „Der Zufall hat kein Gedächtnis.“
Der Spielerfehlschluss wird manchmal als Denkfehler angesehen, der von einem psychologischen, heuristischen Prozess namens Repräsentativitätsheuristik erzeugt wird.
Beispiel: Münzwurf
Der Spielerfehlschluss kann illustriert werden, indem man das wiederholte Werfen einer Münze betrachtet. Als faire Münze gilt eine Münze, bei der die Wahrscheinlichkeiten für „Kopf“ oder „Zahl“ jeweils exakt 0,5 (die Hälfte) betragen. Die Chance für zweimal Kopf hintereinander ist 0,5 × 0,5 = 0,25 (ein Viertel). Die Wahrscheinlichkeit für dreimal Kopf hintereinander ist 0,5 × 0,5 × 0,5 = 0,125 (ein Achtel) usw.
Angenommen, es wäre soeben viermal hintereinander Kopf geworfen worden. Ein Spieler könnte sich sagen: „Wenn der nächste Münzwurf wieder Kopf ergibt, wäre das schon fünfmal Kopf hintereinander. Die Wahrscheinlichkeit für eine solche Reihe ist 0,55 = 0,03125.“ Also denkt man, dass die Chance, dass die Münze das nächste Mal Kopf zeigt, 1 : 32 (= 0,03125) beträgt.
Hier liegt der Fehler. Wenn die Münze fair ist, muss die Wahrscheinlichkeit für „Zahl“ immer 0,5 betragen, nie mehr oder weniger, und die Wahrscheinlichkeit für „Kopf“ muss immer 0,5 sein, nie mehr oder weniger. Die Wahrscheinlichkeit 1:32 für eine Serie von 5 Köpfen gilt nur, bevor man das erste Mal geworfen hat. Die gleiche Wahrscheinlichkeit 1 : 32 gilt auch für viermal hintereinander „Kopf“, gefolgt von einmal „Zahl“ – und jede andere mögliche Kombination. Nach jedem Wurf ist sein Ergebnis bekannt und zählt nicht mehr mit. Jede der beiden Möglichkeiten „Kopf“ oder „Zahl“ hat die gleiche Wahrscheinlichkeit, egal wie oft die Münze bereits geworfen wurde und was dabei herauskam. Der Fehler beruht auf der Annahme, dass frühere Würfe bewirken könnten, dass die Münze eher auf „Kopf“ als auf „Zahl“ fällt, d. h., dass eine vergangene Glückssträhne irgendwie die Wettchancen der Zukunft beeinflussen könnte.
Manchmal argumentieren Spieler, im Hinblick auf das Gesetz der großen Zahlen, so: „Ich habe gerade viermal verloren. Die Münze ist fair, also wird auf lange Sicht alles ausgeglichen. Wenn ich einfach weiterspiele, werde ich mein Geld zurückgewinnen.“ Es ist allerdings irrational, die „lange Sicht“ an dem Punkt zu beginnen, an dem der Spieler zu spielen begann. Genauso gut könnte er auf lange Sicht erwarten, wieder an seiner gegenwärtigen Position (vier Verluste) zu landen.
Mathematisch gesehen beträgt die Wahrscheinlichkeit 1 dafür, dass sich Gewinne und Verluste irgendwann aufheben und dass ein Spieler sein Startguthaben wieder erreicht. Allerdings beträgt der Erwartungswert der dafür notwendigen Spiele unendlich, und auch jener für das einzusetzende Kapital. Ein ähnliches Argument zeigt, dass die populäre Verdopplungsstrategie (beginne mit 1 €; wenn du verlierst, setze 2 €; dann 4 € usw., bis du gewinnst) nicht unbedingt funktioniert (vgl. Martingalespiel, Sankt-Petersburg-Paradoxon). Solche Situationen werden in der mathematischen Theorie der Random walks (wörtlich: Zufallswanderungen) erforscht. Die Verdopplungs- und ähnliche Strategien tauschen entweder viele kleine Gewinne gegen einige große Verluste, oder umgekehrt. Mit Arbeitskapital in unbegrenzter Höhe wären sie erfolgreich. In der Praxis ist es aber vernünftiger, nur einen festen Betrag zu setzen, weil der Verlust pro Tag oder Stunde dann leichter abzuschätzen ist.
Scheinbare Spielerfehlschlüsse
Es gibt viele Szenarien, in denen der Spielerfehlschluss nur auf den ersten Blick vorliegt.
- Wenn die Wahrscheinlichkeiten aufeinanderfolgender Zufallsereignisse nicht unabhängig sind, kann die Chance für zukünftige Ereignisse von vergangenen Ereignissen verändert werden. Ein Beispiel hierfür sind Spielkarten, die ohne Zurücklegen aus einem Stapel gezogen werden. Wurde mit der ersten Karte ein Bube gezogen, ist die Wahrscheinlichkeit dafür, mit der zweiten noch einen zu ziehen, kleiner, als wenn die erste Karte ein Ass war. Der Grund dafür ist, dass nur noch drei Buben vorhanden sind.
- Wenn die Wahrscheinlichkeit der möglichen Ereignisse nicht gleich hoch ist, etwa bei einem gezinkten Würfel, kann ein in der Vergangenheit häufiges Ereignis auch weiterhin gehäuft auftreten (Autokorrelation): die Verfälschung des Würfels favorisiert es. Diese Variante – an die Fairness des Würfels und an die Ehre der Mitspieler zu glauben, obwohl beides fehlt – wurde als Nerd's Gullibility Fallacy (etwa „Leichtgläubigkeit des Fachidioten“) tituliert. Sie ist auch ein Beispiel für Humes Prinzip: Zwanzigmal „Zahl“ hintereinander sprechen eher dafür, dass die Münze gezinkt wurde, als für eine faire Münze, deren nächster Wurf mit gleicher Wahrscheinlichkeit „Kopf“ oder „Zahl“ ergeben wird.
- Die Wahrscheinlichkeiten von zukünftigen Ereignissen können von externen Faktoren beeinflusst werden; z. B. könnten Regeländerungen im Sport die Erfolgschancen einer bestimmten Mannschaft beeinträchtigen.
- Einige Rätsel spiegeln dem Leser vor, sie seien ein Beispiel für den Spielerfehlschluss, beispielsweise das Ziegenproblem (Monty-Hall-Problem).
Bedingungen eines Zufallsexperimentes
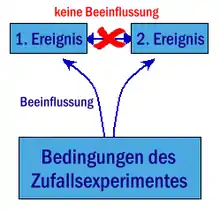
Zu beachten ist, dass sich der Spielerfehlschluss von dem folgenden Gedankengang unterscheidet: Ein Ereignis tritt gehäuft auf, daher ist die angenommene Wahrscheinlichkeitsverteilung anzuzweifeln. Diese Überlegung führt zum entgegengesetzten Schluss, das häufig aufgetretene Ereignis sei wahrscheinlicher. Sie kann korrekt sein, was bei unbekannten Zufallsbedingungen (wie sie in der Realität praktisch immer vorliegen) allerdings stets nur mit einer bestimmten Wahrscheinlichkeit entschieden werden kann.
Weblinks
- Exposing the Gambler's Fallacy (englisch)