Implikation

Die Bezeichnung Implikation (von lateinisch implicare ‚verwickeln‘; Verb: implizieren; Adjektiv: implizit) wird in der Logik nicht einheitlich für einen bestimmten logischen Zusammenhang verwendet, insbesondere werden unterschieden

eine materiale Implikation als eine von mehreren möglichen logischen Verknüpfungen (Junktoren) zwischen zwei Aussagenvariablen: $a\rightarrow b$ (siehe auch Artikel „Junktor“). Diese materiale Implikation, auch Subjunktion oder Konditional genannt, kann wahrheitsfunktional definiert werden (siehe Abschnitt unten). Sie findet sich bereits bei Philon von Megara (3. Jhdt. v. Chr.) und wird umgangssprachlich meist umschrieben mit: „Wenn a, dann b.“[1]
eine formale Implikation als eine Form logischen Zusammenhangs, welche eher einer intuitiven Anschauung entsprechen soll, die sich aus Gewohnheiten der Umgangssprache ergeben kann. Es entstanden im Laufe der Zeit verschiedene Interpretationen, um das Phänomen möglichst eindeutig zu formalisieren. Dabei wird die obige Formel differenzierter betrachtet, zum Beispiel als $\bigwedge _{x}(A(x)\rightarrow B(x))$ , gelesen: „Für jedes Individuum x gilt: Wenn x die Eigenschaft A besitzt, dann besitzt es auch die Eigenschaft B.“ Die Analyse einer Aussage mit Zerlegung in den Prädikator und sein Argument, insbesondere für die formale Implikation, findet sich ähnlich schon bei Platon und Aristoteles.[1]

Als Varianten einer deduktionmäßigen formalen Implikation können auch die intuitionistische Implikation bzw. Subjunktion innerhalb der dialogischen Logik sowie die strenge Implikation von Ackermann und ebenso die strikte Implikation angesehen werden. Von Bruno von Freytag-Löringhoff und Albert Menne wurde die Implikation als hypothetisches Urteil formalisiert.

Diese spezifischeren Deutungen können auch als objektsprachliche Implikationen bezeichnet werden. Davon zu unterscheiden sind dann jeweils die metasprachlichen Implikationen; sie erlauben es, über die logische Struktur dieser Sprachen zu sprechen. Dementsprechend kann ihnen eine noch engere Verbindung zum Ableitbarkeitsbegriff und dem Begriff der Schlussfolgerung zugesprochen werden.

Unterschied zwischen objektsprachlicher und metasprachlicher Implikation

Die objektsprachliche Implikation (materiale Implikation, Konditional, Subjunktion) ist ein Aussagesatz, der mittels des Junktors „(schon) wenn …, dann …“ aus zwei kürzeren Aussagesätzen zusammengesetzt ist. Zum Beispiel ist „Wenn es regnet, dann ist die Straße nass“ eine materiale Implikation; diese Implikation sagt etwas über den logischen Zusammenhang der Sätze, nämlich dass die Wahrheit des ersten Teilsatzes (Antezedens, auch Antecedens) eine hinreichende Bedingung für die Wahrheit des zweiten Teilsatzes (Konsequenz) ist.

Die metasprachliche Implikation ist hingegen eine Aussage über Aussagen, eben eine Metaaussage. Eine metasprachliche Implikation wäre die Aussage „Aus dem Satz ‚Es regnet‘ folgt der Satz ‚Die Straße ist nass‘“. Hier wird nichts über Regen, Nässe oder deren Zusammenhang ausgesagt, sondern hier wird über zwei Sätze der Objektsprache und ihr logisches Verhältnis gesprochen. Dabei kann auf ihre Bedeutung Bezug genommen werden (etwa: ob das, was der eine Satz aussagt, vorliegt, wenn das vorliegt, was der andere aussagt) oder auch nicht, so können zwei Sätze allein durch ihre logische Form miteinander verbunden sein (so kann man zum Beispiel sagen: „Wenn $a\land b$ , dann $a$ “).

Objektsprachliche Implikationen

Die objektsprachliche Implikation, ein Aussagesatz, der mittels des Junktors „(schon) wenn …, dann …“ aus zwei kürzeren Aussagesätzen zusammengesetzt ist, wird als materiale Implikation, Subjunktion und Konditional bezeichnet.

Wahrheitsfunktionale Implikation

Die Subjunktion ist nur dann falsch, wenn A wahr und B falsch ist. Dieser Bereich ist im Venn-Diagramm weiß.
Es gilt klassisch

A\rightarrow B\Leftrightarrow \neg A\lor B

\Leftrightarrow

\lor

In der klassischen Logik werden nur wahrheitsfunktionale Aussageverbindungen verwendet, das heißt nur solche, bei denen der Wahrheitswert der Aussagenverknüpfung allein von dem Wahrheitswert der Teilaussagen abhängt. Innerhalb eines Konditionals $a\rightarrow b$ wird die erste Aussage $a$ unter anderem als Vordersatz, Antezedens, Implikans oder Vorderglied bezeichnet, die zweite Aussage $b$ unter anderem als Nachsatz, Hintersatz, Konsequenz, Implikat, selten auch Sukzedens.

Seit der Antike wird – erstmals von Philon von Megara – die wahrheitsfunktionale Implikation oder seq-Funktion durch folgende Wahrheitstabelle definiert:

$a$	$b$	$a\rightarrow b$
f	f	w
f	w	w
w	f	f
w	w	w

Diese wahrheitsfunktionale objektsprachliche Implikation wird unter anderem materiale Implikation, Subjunktion oder (zunehmend) Konditional genannt. Sie drückt die hinreichende Bedingung aus, das heißt, sie behauptet keinerlei kausalen oder sonstigen inhaltlichen Zusammenhang zwischen $A$ und $B$ .

Schon im Altertum wurde diskutiert, inwieweit und unter welchen Voraussetzungen das natürlichsprachliche „wenn …, dann …“ eine hinreichende Bedingung ausdrückt und damit der materialen Implikation entspricht, vor allem aber, ob und wie sich die anderen Bedeutungen des natürlichsprachlichen „wenn …, dann …“, zum Beispiel die kausale („A verursacht B“), analysieren lassen. Versuche, andere Bedeutung als die rein wahrheitsfunktionale („materiale“) Bedeutung des natürlichsprachlichen „wenn …, dann …“ zu analysieren, führen zu nichtklassischen Implikationen, zum Beispiel der strikten Implikation und der intuitionistischen Implikation.

Als Symbol für den Junktor wird in der formalen Sprache der Logik ein einfacher Pfeil $\rightarrow$ , insbesondere im englischsprachigen Bereich in Anlehnung an die Peano-Russellsche Schreibweise auch die Kurve $\supset$ („Hufeisen“, „horseshoe“, „Bogenzeichen“ (Reichenbach)) verwendet, gelegentlich auch der Pfeil mit zwei Querstrichen $\Rightarrow$ .

In der polnischen Notation wird für die materiale Implikation der Großbuchstabe C verwendet, sodass die Aussage „Wenn a, dann b“ als Cab geschrieben wird.

Gottlob Frege drückt in seiner Begriffsschrift, der ersten Formalisierung der klassischen Prädikatenlogik, das Konditional „Wenn A, dann B“ durch 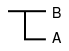aus.

Schreibweisen	$a\rightarrow b$	$a\supset b$	$a\Rightarrow b$	$Cab$

Natürliche Sprache und materiale Implikation

Im Fall der materialen Implikation sagt man oft kurz: „Wenn a, dann b.“ Dieser Sprachgebrauch ist etwas unglücklich, weil die Formulierung „wenn …, dann …“ im Deutschen ein weites Bedeutungsfeld hat und mehrheitlich nicht für materiale, das heißt hier wahrheitsfunktionale, sondern für inhaltliche Zusammenhänge (Kausalität oder zeitliche Abfolge) verwendet wird. Solche Zusammenhänge lassen sich mit der materialen Implikation nicht ausdrücken. Zwischen der materialen Implikation und dem natürlichsprachlichen „wenn …, dann ...“ muss daher sehr genau unterschieden werden. Manchmal versucht man, durch Formulierungen wie „Schon wenn a, dann b …“ oder „a ist eine hinreichende Bedingung für b“ Missverständnisse zu vermeiden, die aus den vielen Bedeutungen des deutschen „wenn …, dann …“ resultieren können.

Die Implikation zu (a) „Es regnet“ und (b) „Die Straße wird nass“ ist damit die Aussage

Wenn es regnet, wird die Straße nass.

Alternative Formulierungen, die den materialen Charakter besser betonen, sind

Schon wenn es regnet, wird die Straße nass.

oder

Dass es regnet, ist eine hinreichende Bedingung dafür, dass die Straße nass wird.

Die materiale Implikation ist genau dann falsch, wenn das Antezedens wahr ist und das Sukzedens falsch ist. In jedem anderen Fall ist die Implikation wahr. Das Konditional „Wenn es regnet, wird die Straße nass“ ist also nur dann falsch, wenn es regnet, die Straße aber nicht nass wird.

Die Festlegung, dass eine materiale Implikation nur dann falsch ist, wenn das Antezedens (der Wenn-Teil) wahr und das Sukzedens falsch ist, führt dazu, dass die folgenden Verknüpfungen empirischer Aussagen wahr sind:

Wenn London in Frankreich liegt, ist Schnee weiß.	falsches Antezedens, wahres Sukzedens
Wenn London in Frankreich liegt, ist Schnee schwarz.	falsches Antezedens, falsches Sukzedens
Wenn London in England liegt, ist Schnee weiß.	wahres Antezedens, wahres Sukzedens

Diese Paradoxien der materialen Implikation unterstreichen den extensionalen Charakter (siehe Junktor) der materialen Implikation: Sie behauptet keinerlei inhaltlichen Zusammenhang zwischen Antezedens (Wenn-Teil) und Sukzedens (es gibt auch tatsächlich keinen Zusammenhang zwischen der geographischen Lage von London und der Farbe von Schnee), vielmehr wird ihr Wahrheitswert rein extensional auf die Wahrheitswerte ihrer Teilsätze zurückgeführt: „Schon wenn das Antezedens wahr ist, ist das Sukzedens auch wahr.“

Zusammenhang mit der notwendigen Bedingung

Wie bereits erwähnt, drückt die materiale Implikation die hinreichende Bedingung aus. Von ihr zu unterscheiden ist die notwendige Bedingung, die besagt, dass ein Sachverhalt erforderlich, aber eben nicht ausreichend dafür ist, dass ein anderer Sachverhalt eintritt.

Beispiel: „Nur wenn eine Person volljährig ist, darf sie wählen.“ Volljährigkeit ist eine notwendige Bedingung für das Wahlrecht, ist aber nicht ausreichend; man muss in der Regel zusätzliche Bedingungen erfüllen, z. B. die Staatsbürgerschaft des Landes haben.

Die hinreichende und die notwendige Bedingung stehen in engem Zusammenhang. Wenn ein Sachverhalt A eine hinreichende Bedingung für einen Sachverhalt B ist, dann ist B zugleich eine notwendige Bedingung für A. Das Beispiel „Nur wenn eine Person volljährig ist, darf sie wählen“ ist logisch äquivalent mit „Schon wenn eine Person wählen darf, ist sie volljährig.“ Verdeutlichen kann man sich diesen zunächst oft als kontraintuitiv empfundenen Zusammenhang, indem man sich die Situation in einem Wahllokal vor Augen führt. Wenn man dort eine Person wählen sieht, dann kann man – auch wenn sie vielleicht sehr jung aussieht – daraus eindeutig schließen, dass sie volljährig sein muss; denn es dürfen ja nur Volljährige wählen.

Auf Grund dieses inhaltlichen Zusammenhangs drückt die materiale Implikation ebenso die notwendige wie die hinreichende Bedingung aus:

A\rightarrow B

wird zwar gewöhnlich gelesen als „A ist eine hinreichende Bedingung für B“ bzw. „Schon wenn A, dann B“; da das aber äquivalent ist zu „B ist eine notwendige Bedingung für A“, kann man es ebenso gut auf diese Weise lesen.

Eigenschaften und logische Gesetze

Die materiale Implikation

a\rightarrow b

ist aussagenlogisch zum Beispiel mit den folgenden Aussagen äquivalent:

$\neg a\lor b$ (lies: „nicht a oder b“). Über diese Äquivalenz kann die materiale Implikation anhand von Disjunktion und Negation definiert werden.
$\neg (a\land \neg b)$ (lies: „es gilt nicht: a und nicht b“). Die materiale Implikation kann also ebenfalls anhand von Konjunktion und Negation definiert werden.
$\neg b\rightarrow \neg a$ (lies: „wenn nicht b, dann nicht a“). Man kann also die Implikation umkehren, wenn man dabei gleichzeitig Antezedenz und Sukzedenz negiert. Dieses logische Gesetz wird auch als Kontraposition bezeichnet.

Außerdem ist die Aussage a äquivalent mit $\top \rightarrow a$ und die Aussage $\neg a$ (lies: „nicht a“) ist äquivalent mit $a\rightarrow \bot$ , wobei $\top$ eine beliebige Tautologie und $\bot$ eine beliebige Kontradiktion ist. Ferner sind $\bot \rightarrow a$ und $a\rightarrow \top$ äquivalent mit $\top$ .

Aufgrund ihres extensionalen Charakters eignet sich die materiale Implikation in der Prädikatenlogik gut dazu, Aussagen des Typs „Alle Pferde sind Säugetiere“ wie folgt zu formalisieren:

Schreibweise	$\forall x(P(x)\rightarrow S(x))$
Sprechweise	„Für alle x gilt: Wenn x ein Pferd ist, ist x ein Säugetier“

Bezüglich der Eigenschaften der materialen Implikation ist festzuhalten: Sie ist nicht assoziativ, kommutativ, symmetrisch, antisymmetrisch oder asymmetrisch. Sie ist aber transitiv, das heißt, es gilt:

aus

a\rightarrow b

und

b\rightarrow c

folgt

a\rightarrow c

Außerdem ist sie reflexiv, es gilt also allgemein:

a\rightarrow a

Mit Hilfe der Implikation und der Negation lassen sich alle aussagenlogischen Junktoren darstellen.

Intuitionistische Implikation

Im Intuitionismus bedeutet der Ausdruck $a\rightarrow b$ , dass sich ein Beweis von $a$ (über dessen Existenz nichts ausgesagt wird) zu einem Beweis von $b$ ergänzen lässt. Diese Beziehung kann nicht anhand der Wahrheitswerte von Antezedens und Sukzedens definiert werden, sie ist also nicht extensional oder wahrheitsfunktional. Stattdessen werden intensionale Semantiken verwendet, deren bekannteste und erste formalisierte die von Saul Aaron Kripke zunächst für die Modallogik entwickelte Kripke-Semantik ist.

Die oben angeführten Äquivalenzen gelten intuitionistisch teilweise „nur in eine Richtung“, d. h. insbesondere:

aus $a\rightarrow b$ folgt $\neg (a\land \neg b)$ , aber nicht umgekehrt.
aus $a\rightarrow b$ folgt $\neg b\rightarrow \neg a$ , aber nicht umgekehrt.
aus $\neg a\lor b$ folgt $a\rightarrow b$ , aber nicht umgekehrt.

Anders als die materiale Implikation kann also die intuitionistische Implikation nicht über Negation und Konjunktion oder Disjunktion definiert werden.

Es gilt jedoch weiterhin, dass a äquivalent ist mit $\top \rightarrow a$ und $\neg a$ mit $a\rightarrow \bot$ sowie dass $\bot \rightarrow a$ und $a\rightarrow \top$ äquivalent sind mit $\top$ . Wie die materiale Implikation ist auch die intuitionistische transitiv und reflexiv.

Strikte Implikation

Bei der strikten Implikation handelt es sich um die Kombination des modallogischen Notwendigkeits-Operators mit der materialen Implikation.

Schreibweise	$\Box (a\rightarrow b)$ , $\Box (a\supset b)$
Sprechweise	Wenn a, dann gilt notwendig b

Die strikte Implikation wurde von Diodoros Kronos und in der Scholastik als Umgehungsversuch der Paradoxien der materialen Implikation entwickelt und 1918 von Clarence Irving Lewis neu aufgestellt. Damit soll eine Annäherung an das natürlichsprachliche „wenn …, dann …“ erreicht werden. Die strikte Implikation ist nämlich nicht schon dann bereits wahr, wenn das Antezedens falsch oder das Sukzedens wahr ist. Von der strikten Implikation gibt es zahlreiche Varianten, je nachdem welcher Modalkalkül zugrunde gelegt wird. Die strikte Implikation ist, ebenso wie die materiale und die intuitionistische, transitiv und reflexiv.

Auch das Konzept der strikten Implikation unterliegt der Kritik, weil sie zwar die Paradoxie der materialen Implikation vermeidet, aber zu der analogen Schwierigkeit führt, dass jede logisch unmögliche Aussage jede beliebige Aussage und dass jede Aussage jede logisch notwendige Aussage strikt impliziert. Lewis' eigener Verwendung der strikten Implikation wurde zudem vorgeworfen, Objekt- und Metasprache durcheinanderzubringen.

Metasprachliche Implikation

Die metasprachliche Implikation ist eine Aussage über Aussagen. Eine Aussage A impliziert genau dann eine Aussage B, wenn mit dem Zutreffen von A auch das Zutreffen von B gewährleistet ist. Analog implizieren mehrere Aussagen A₁ bis A_n genau dann eine Aussage B, wenn mit dem gemeinsamen Zutreffen der Aussagen A₁ bis A_n auch das Zutreffen von B gewährleistet ist. Zum Beispiel implizieren die Aussagen „Alle Schweine grunzen“ und „Babe ist ein Schwein“ die Aussage „Babe grunzt“.

Der Begriff der Folgerung und damit die metasprachliche Implikation wird auf unterschiedliche Weisen formal präzisiert. Zum einen unterscheidet man zwischen der semantischen Folgerung, aufgeschrieben als $A_{1},\ldots ,A_{n}\models B$ , und der syntaktischen Folgerung, der Herleitbarkeit, aufgeschrieben als $A_{1},\ldots ,A_{n}\vdash B$ :

Semantischer Folgerungsbegriff: Eine Folgerung ist genau dann semantisch gültig, geschrieben: $A_{1},\ldots ,A_{n}\models B$ , wenn die Wahrheit der Aussagen A₁ bis A_n die Wahrheit der Aussage B gewährleistet. In einer Interpretationssemantik ist das genau dann der Fall, wenn bei jeder Interpretation, bei der jede der Aussagen A₁ bis A_n wahr ist, auch die Aussage B wahr ist.
Syntaktischer Folgerungsbegriff: Eine Folgerung ist genau dann syntaktisch gültig, geschrieben $A_{1},...A_{n}\vdash B$ , wenn sich die Aussage B in einem gegebenen logischen Kalkül aus den Aussagen A₁ bis A_n herleiten lässt, das heißt, wenn sich aus den Aussagen A₁ bis A_n unter Anwendung der Schlussregeln und Axiome des jeweiligen Kalküls die Aussage B erzeugen lässt.

Zum anderen gibt es grundsätzlich unterschiedliche Fassungen des Folgerungsbegriffs und damit der metasprachlichen Implikation, etwa den der klassischen Logik oder den der Logik. Diese unterschiedlichen Definitionen von Folgerung beziehungsweise metasprachlicher Implikation führen zu grundsätzlich unterschiedlichen Kalkülen und semantischen Modellen. Wenn aus dem Zusammenhang nicht klar hervorgeht, welche Art von metasprachlicher Implikation beziehungsweise Folgerung gemeint ist, ist es daher notwendig, diese Information mitzuliefern. Man kann daher zum Beispiel auf Formulierungen treffen wie „A impliziert klassisch (semantisch, syntaktisch) B“ oder „C impliziert intuitionistisch (semantisch, syntaktisch) D“. In der formalen Schreibweise wird die Art der Folgerung meist durch ein Subskript beim Folgerungszeichen angezeigt. So könnte zum Beispiel „K“ für klassische, „I“ für intuitionistische Folgerung stehen, also $A\models _{K}B$ (semantisch, klassisch), $A\vdash _{K}B$ (syntaktisch, klassisch), $A\models _{I}B$ (semantisch, intuitionistisch) und $A\vdash _{I}B$ (syntaktisch, intuitionistisch).

In den allermeisten Logiken besteht zwischen objekt- und metasprachlicher Implikation ein enger Zusammenhang, der im Deduktionstheorem ausgedrückt wird. Ist nämlich „Wenn a, dann b“ beweisbar, so lässt sich b aus a herleiten; und lässt sich umgekehrt b aus a herleiten, dann ist „Wenn a, dann b“ beweisbar. Für „c ist beweisbar“ schreibt man auch $\vdash c$ . Das Deduktionstheorem kann damit wie folgt niedergeschrieben werden:

\vdash a\rightarrow b

gdw.

a\vdash b

Das Deduktionstheorem gilt sowohl für die klassische, die intuitionistische als auch die strikte Implikation. Es handelt sich jedoch um keinen selbstverständlichen Zusammenhang, sondern erfordert einen (in den meisten Fällen nicht-trivialen) Beweis.

Siehe auch

Weblinks

Wiktionary: Implikation – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen

Dorothy Edgington: Conditionals. In: Edward N. Zalta (Hrsg.): Stanford Encyclopedia of Philosophy.
Andrew Brennan: Necessary and Sufficient Conditions. In: Edward N. Zalta (Hrsg.): Stanford Encyclopedia of Philosophy.
Horacio Arlo-Costa: The Logic of Conditionals. In: Edward N. Zalta (Hrsg.): Stanford Encyclopedia of Philosophy.

Einzelnachweise

Grundriß der formalen Logik. Paderborn: Universitäts-Taschen-Bücher-Verlag: 1983. Aus dem Französischen von Joseph Maria Bocheński. Von Albert Menne übersetzt und erweitert.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[Grundriß_der_formalen_Logik-1] Grundriß der formalen Logik. Paderborn: Universitäts-Taschen-Bücher-Verlag: 1983. Aus dem Französischen von Joseph Maria Bocheński. Von Albert Menne übersetzt und erweitert.