Diffusivität

Diffusivität (von lateinisch diffundere „ausdehnen, zerstreuen; ausströmen lassen“) ist die Eigenschaft eines Materials, die Ausbreitung von gelösten Stoffen zu ermöglichen. Der Ausbreitungsprozess selbst wird als Diffusion bezeichnet.

Der Begriff steht einerseits für den Diffusionskoeffizienten,[1] aber insbesondere in festem Material im übertragenen Sinne für die Fähigkeit, Diffusion zuzulassen. In der übertragenen Bedeutung wird er insbesondere in den Neurowissenschaften im Zusammenhang mit Körpergewebe und der in ihr enthaltenen Gewebsflüssigkeit verwendet, aber auch in der Hydrologie (Grundwasser), der Festkörperphysik und der Thermodynamik (Wärmediffusivität).

Im Gegensatz zur Diffusion in flüssigen oder gasförmigen Medien kann sich ein gelöster Stoff im Festkörper (z. B. wegen der Kristallgitter-Struktur), aber auch Flüssigkeit in festem Material (z. B. wegen Bodenschichten, Nervenfasern) im Allgemeinen nicht in alle Richtungen gleichermaßen ausbreiten. Bestimmte Richtungen werden bevorzugt und es herrscht Anisotropie. In diesem Falle steht im 1. Fickschen Gesetz anstelle des Diffusionskoeffizienten der Diffusionstensor (eine symmetrische 3×3-Matrix mit reellen nichtnegative Eigenwerten).

Die richtungsabhängige Ausbreitung im Gewebe wird als scheinbare Diffusion bezeichnet, die Hauptdiagonalelemente des Diffusions-Tensors als scheinbare Diffusionskoeffizienten (auch ADC für apparent diffusion coefficient). Zur quantitativen Beschreibung der scheinbaren Diffusion und der damit verbundenen Anisotropie werden verschiedene Maßzahlen verwendet, die unter anderem aus den Eigenwerten des Diffusionstensors gebildet werden. So misst z. B. die fraktionale Anisotropie (FA), wie stark die Eigenwerte sich voneinander unterscheiden, d. h., wie stark sich die Diffusivität in verschiedenen Richtungen unterscheidet. Die fraktionale Anisotropie und die relative Anisotropie (RA) werden zusammen mit mittlerer, axialer und radialer Diffusivität weiter unten behandelt.

In geisteswissenschaftlichen Disziplinen wird der Begriff übertragen für den Grad gebraucht, in dem sich etwas ausbreiten oder verschoben bzw. auf andere Gebiete angewandt werden kann.[2][3][4]

Hintergrund

Diffusion von gelösten Stoffen wird durch die Fickschen Gesetze beschrieben. Das erste dieser beiden Gesetze

j=-D{\frac {\partial c}{\partial x}}

sagt aus, das die Teilchenstromdichte $j$ linear vom Gradienten der Konzentration $c$ abhängt: je größer an zwei Orten der Unterschied in der Konzentration des gelösten Stoffes ist, desto mehr Teilchen werden von der höheren zur niedrigeren Konzentration fließen. Der Koeffizient $D$ wird dabei der Diffusionskoeffizient oder die Diffusivität genannt.

Diese Beschreibung kann für verschiedenste Transportprozesse angewandt werden, die von in Flüssigkeiten gelösten chemischen Stoffen, über elektrische Leitung bis hin zur Wärmeleitung reichen.

Die einfache Beschreibung durch das eindimensionale Gesetz oben bricht jedoch immer dann zusammen, wenn der Transport in bestimmten Richtungen bevorzugt ablaufen kann, in anderen aber behindert wird. Man spricht dann von Richtungsabhängigkeit oder Anisotropie.

Mögliche Gründe für eine Anisotropie können sein, dass bestimmte Stellen im Festkörper größere Konzentrationen des gelösten Stoffes aufnehmen können. So können sich in Stahl an der Rissspitze von Versetzungen höhere Konzentrationen von gelöstem Wasserstoff ansammeln.[5] Auch bei der Beschreibung der Wärmeleitung spielen Unterschiede der Wärmekapazität des Materials eine Rolle, weshalb zwischen der Temperaturleitfähigkeit (die auch Wärmediffusivität genannt wird) und der Wärmeleitfähigkeit unterschieden werden muss.

Viel drastischer ist die Richtungsabhängigkeit jedoch in Körpergewebe, in dem bereits in gesundem Gewebe Zellmembranen den freien Fluss der Gewebsflüssigkeit behindern.[6]

Im Falle von Anisotropie tritt an die Stelle des obigen eindimensionalen Gesetzes

{\vec {j}}=-{\overline {\overline {D}}}\nabla c\ ,

in dem nun

{\overline {\overline {D}}}={\begin{bmatrix}D_{x}&D_{xy}&D_{xz}\\D_{yx}&D_{y}&D_{yz}\\D_{zx}&D_{zy}&D_{z}\end{bmatrix}}

eine 3×3-Matrix ist, die als Diffusions-Tensor bezeichnet wird. Diese Matrix ist symmetrisch und hat daher nur sechs unabhängige Komponenten, die in einer Variante der Voigtschen Notation als ein Vektor

{\overline {D}}=(D_{x},D_{xy},D_{xz},D_{y},D_{yz},D_{z})^{T}

geschrieben werden können.

Die Eigenwerte des Diffusions-Tensors werden mit $\lambda _{1}$ , $\lambda _{2}$ und $\lambda _{3}$ bezeichnet, wobei λ₁ ≥ λ₂ ≥ λ₃ ≥ 0 gilt. Trägt man die scheinbaren Diffusionskoeffizienten über den jeweiligen Raumrichtungen auf, so erhält man im Allgemeinen einen Rotationsellipsoid.

Messung und Anwendung

Die Messung der Diffusivität erfolgt mit Hilfe von Magnetresonanzbildgebung (MRI) bei der so genannten Diffusionstensorbildgebung (DTI) so, dass das Gehirn in 0,5–8 mm³ große Voxel eingeteilt wird und in jedem Voxel in mindestens sechs verschiedene Richtungen je der Diffusionskoeffizient der Selbstdiffusion von Wasser in der Gewebsflüssigkeit gemessen wird. Ein solcher Diffusionskoeffizient wird denn auch als scheinbarer Diffusionskoeffizient (auch ADC für apparent diffusion coefficient) bezeichnet. Auf Grund dieser mindestens 6 Werte pro Voxel wird für jedes Voxel ein Diffusionstensor berechnet. Aus diesem werden voxelweise Maßzahlen für die Diffusivität oder Anisotropie abgeleitet und z. B. mit Hilfe von Tensor-Glyphen oder als Farbwertbilder grafisch dargestellt oder für weitergehende Auswertungen verwendet, z. B. die Erstellung von Modellen der Fasertrakte (Traktographie).

Auf Grund der Diffusivität kann auf andere Eigenschaften des Gewebes geschlossen werden. So werden Rückschlüsse auf die grobe Struktur (z. B. Faserigkeit) und damit auf alterungs- oder krankheitsbedingte Veränderungen (z. B. Veränderungen der Myelinisierung der Axone) von Hirngewebe gezogen. Da die Beweglichkeit von Gewebeflüssigkeit in faserigem Gewebe in Richtung der Gewebefasern wesentlich größer ist als quer zur Faserrichtung können auf Grund von Diffusivitätsmessungen Modelle der Fasertrakte des Gehirns erstellt werden (Traktografie). Es kann aber auch festgestellt werden, an welcher Stelle aufgrund des Bruchs einer Membran Flüssigkeit frei fließen kann.

Maßzahlen

Die Diffusivität wird mit den Eigenwerten des Diffusionstensors beschrieben, wobei dabei die mittlere Diffusivität ${\overline {\lambda }}$ , die axiale Diffusivität $\lambda _{a}$ und die radiale Diffusivität $\lambda _{t}$ hervorgehoben werden.

Um den Grad der Anisotropie zu beschreiben bildet man aus den Eigenwerten darüber hinaus die skaleninvarianten Verhältnisse

fraktionale Anisotropie $FA$
relative Anisotropie $RA$
Volumenverhältnis $VR$

Mittlere Diffusivität

Die mittlere Diffusivität (der mittlere Diffusionskoeffizient) ist definiert als

{\overline {\lambda }}:={\frac {\lambda _{1}+\lambda _{2}+\lambda _{3}}{3}}

(= Mittelwert der 3 Eigenwerte)

Er kann theoretisch beliebig groß sein, was entsprechend beliebig große Diffusivität bedeuten würde. ${\overline {\lambda }}=0$ für völliges Fehlen scheinbarer Diffusion (keine Brownsche Bewegung der gemessenen Moleküle).

Axiale Diffusivität

Die axiale Diffusivität $\lambda _{a}:=\lambda _{1}$ ist der größte der drei Eigenwerte.

Anschaulicher: Die axiale Diffusivität $\lambda _{a}$ ist die Länge des Diffusionstensorellipsoids und beschreibt damit die Stärke der scheinbaren Diffusion in der Hauptrichtung, also der Richtung der größten Beweglichkeit. Sie ist ein Marker für die axonale Unversehrtheit. Je größer die axiale Diffusivität, desto unversehrter sind die Axone.

Radiale Diffusivität

Die radiale Diffusivität ist der Mittelwert der beiden kleineren Eigenwerte, also $\lambda _{t}:={\frac {\lambda _{2}+\lambda _{3}}{2}}$ Anschaulicher: Die radiale Diffusivität λ_t (t für transversal) ist die durchschnittliche Dicke des Diffusionstensorellipsoids in der Längsmitte und beschreibt die durchschnittliche scheinbare Diffusion in der Ebene senkrecht zur Hauptrichtung. Sie ist zum Beispiel ein Marker für die Unversehrtheit von Myelin. Demyelinisierung erhöht die radiale Diffusivität.

Fraktionale Anisotropie

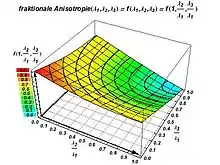
Fraktionale Anisotropie als Funktion der Eigenwerte eines Diffusionstensors

Die fraktionale Anisotropie ist definiert als

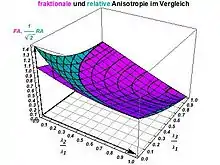
FA:={\sqrt {\frac {3((\lambda _{1}-{\overline {\lambda }})^{2}+(\lambda _{2}-{\overline {\lambda }})^{2}+(\lambda _{3}-{\overline {\lambda }})^{2})}{2(\lambda _{1}^{2}+\lambda _{2}^{2}+\lambda _{3}^{2})}}}={\sqrt {\frac {(\lambda _{1}-\lambda _{2})^{2}+(\lambda _{2}-\lambda _{3})^{2}+(\lambda _{3}-\lambda _{1})^{2}}{2(\lambda _{1}^{2}+\lambda _{2}^{2}+\lambda _{3}^{2})}}}

Anschaulicher: Die fraktionale Anisotropie FA ist die Standardabweichung der Eigenwerte dividiert durch die Frobeniusnorm des Diffusionstensors. Sie ist ein Maß für die Gerichtetheit der scheinbaren Diffusion. Es ist FA = 0 im Falle von vollständiger Isotropie, d. h. λ₁ = λ₂ = λ₃ > 0. Bei maximaler Anisotropie (vollständiger Gerichtetheit der Diffusion in genau eine Richtung), wenn also λ₁ > 0 und λ₂ = λ₃ = 0 sind, ist FA = 1. Sie ist zum Beispiel ein Marker für die anatomische Beschaffenheit der weißen Substanz des Hirns: Je größer die FA, desto unversehrter die weiße Substanz.

Relative Anisotropie

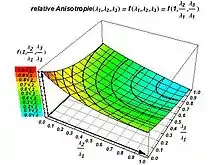
Relative Anisotropie als Funktion der Eigenwerte eines Diffusionstensors

Fraktionale und relative Anisotropie im Vergleich

Die relative Anisotropie ist definiert als

RA:={\frac {\sqrt {\frac {(\lambda _{1}-{\overline {\lambda }})^{2}+(\lambda _{2}-{\overline {\lambda }})^{2}+(\lambda _{3}-{\overline {\lambda }})^{2}}{3}}}{\overline {\lambda }}}

Anschaulicher: Die relative Anisotropie RA ist die Standardabweichung der Eigenwerte (gerechnet als Standardabweichung einer Grundgesamtheit, also mit n = 3 als Divisor) dividiert durch den Mittelwert der Eigenwerte. Sie ist ein Maß für die Gerichtetheit der scheinbaren Diffusion. Es ist RA = 0 im Falle von vollständiger Isotropie, d. h. λ₁ = λ₂ = λ₃ > 0. Bei maximaler Anisotropie (vollständiger Gerichtetheit der Diffusion in genau eine Richtung), wenn also λ₁ > 0 und λ₂ = λ₃ = 0 sind, ist RA = ${\sqrt {2}}$ .

Volumenverhältnis

Volumenverhältnis als Funktion der Eigenwerte eines Diffusionstensors

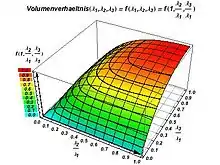
Das Volumenverhältnis ist definiert als

VR:={\frac {\lambda _{1}\lambda _{2}\lambda _{3}}{{\overline {\lambda }}^{3}}}

Anschaulicher: Das Volumenverhältnis VR ist das Produktes der Eigenwerte dividiert durch die 3. Potenz des Mittelwertes der Eigenwerte. Es ist ein Maß für die Gerichtetheit der scheinbaren Diffusion. Es ist VR = 1 im Falle von vollständiger Isotropie, d. h. λ₁ = λ₂ = λ₃ > 0. Wenn mindestens der kleinste der Eigenwerte gleich 0 ist, dann ist VR = 0. Das entspricht der Situation, dass die Diffusion nur in genau einer Richtung (λ₂ = λ₃ = 0) oder aber nur in einer Ebene (λ₃ = 0) stattfindet.

Literatur

Scott A. Huettel, Allen W. Song, Gregory McCarthy: Functional magnetic resonance imaging. Sinauer Associates, Sunderland, Mass. 2008, ISBN 978-0-87893-286-3 (Englischsprachiges Fachbuch, erklärt in Kapitel 5 die Diffusionstensorbildgebung).
Derek K. Jones: Gaussian Modeling of the Diffusion Signal. In: Heidi Johansen-Berg, Timothy E. J. Behrens (Hrsg.): Diffusion MRI: from quantitative measurement to in-vivo neuroanatomy. Academic Press, London 2009, ISBN 978-0-12-374709-9, S. 37–54 (eingeschränkte Vorschau in der Google-Buchsuche – Kapitel 3 in englischsprachigem Fachbuch).
Le Bihan D, Mangin JF, Poupon C, Clark CA, Pappata S, Molko N, Chabriat H: Diffusion Tensor Imaging: Concepts and Applications. In: Journal of Magnetic Resonance Imaging. 2001, S. 534–546 (englisch, Diffusion Tensor Imaging: Concepts and Applications (Memento vom 19. Oktober 2013 im Internet Archive) [PDF; 696 kB; abgerufen am 22. Juni 2016] Übersichts-Artikel in Fachzeitschrift).

Einzelnachweise

Charles Kittel: Thermodynamik. Oldenbourg, München 2001, ISBN 3-486-25716-1, S. 391 (eingeschränkte Vorschau in der Google-Buchsuche).
Kurt Krenn: Vermittlung und Differenz? Vom Sinn des Seins in der Befindlichkeit der Partizipation beim Hl. Thomas von Aquin (= Analecta Gregoriana. Band 121). Editrice Pontificia Università Gregoriana, Rom 1962, ISBN 978-88-7652-094-5, S. 76, 78 (eingeschränkte Vorschau in der Google-Buchsuche).
Gabriele Fassauer: Arbeitsleistung, Identität und Markt - Eine Analyse marktförmiger Leistungssteuerung in Arbeitsorganisatione. VS Verlag für Sozialwissenschaften, Wiesbaden 2008, ISBN 978-3-531-15950-8, S. 238 (eingeschränkte Vorschau in der Google-Buchsuche).
Daniel Fulda: Wissenschaft aus Kunst - Die Entstehung der modernen deutschen Geschichtsschreibung 1760-186. W. de Gruyter, Berlin / New York 1996, ISBN 978-3-11-015014-8, S. 227 (eingeschränkte Vorschau in der Google-Buchsuche).
Guido Juilfs: Das Diffusionsverhalten von Wasserstoff in einem niedriglegierten Stahl unter Berücksichtigung des Verformungsgrades. GRIN Verlag, München 2008, ISBN 978-3-640-20251-5, S. 11 (eingeschränkte Vorschau in der Google-Buchsuche).
Timo Krings: Grundlagen der funktionellen Magnetresonanztomographie. In: Günter Schiepek, Canan Basar (Hrsg.): Neurobiologie der Psychotherapie. Schattauer, Stuttgart 2004, ISBN 3-7945-2363-6, S. 104–130, insbesondere S. 124 (eingeschränkte Vorschau in der Google-Buchsuche).

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[Kittel-1] Charles Kittel: Thermodynamik. Oldenbourg, München 2001, ISBN 3-486-25716-1, S. 391 (eingeschränkte Vorschau in der Google-Buchsuche).

[Krenn-2] Kurt Krenn: Vermittlung und Differenz? Vom Sinn des Seins in der Befindlichkeit der Partizipation beim Hl. Thomas von Aquin (= Analecta Gregoriana. Band 121). Editrice Pontificia Università Gregoriana, Rom 1962, ISBN 978-88-7652-094-5, S. 76, 78 (eingeschränkte Vorschau in der Google-Buchsuche).

[Fassauer-3] Gabriele Fassauer: Arbeitsleistung, Identität und Markt - Eine Analyse marktförmiger Leistungssteuerung in Arbeitsorganisatione. VS Verlag für Sozialwissenschaften, Wiesbaden 2008, ISBN 978-3-531-15950-8, S. 238 (eingeschränkte Vorschau in der Google-Buchsuche).

[Fulda-4] Daniel Fulda: Wissenschaft aus Kunst - Die Entstehung der modernen deutschen Geschichtsschreibung 1760-186. W. de Gruyter, Berlin / New York 1996, ISBN 978-3-11-015014-8, S. 227 (eingeschränkte Vorschau in der Google-Buchsuche).

[Juilfs-5] Guido Juilfs: Das Diffusionsverhalten von Wasserstoff in einem niedriglegierten Stahl unter Berücksichtigung des Verformungsgrades. GRIN Verlag, München 2008, ISBN 978-3-640-20251-5, S. 11 (eingeschränkte Vorschau in der Google-Buchsuche).

[Krings-6] Timo Krings: Grundlagen der funktionellen Magnetresonanztomographie. In: Günter Schiepek, Canan Basar (Hrsg.): Neurobiologie der Psychotherapie. Schattauer, Stuttgart 2004, ISBN 3-7945-2363-6, S. 104–130, insbesondere S. 124 (eingeschränkte Vorschau in der Google-Buchsuche).