Differenzengleichung (Differenzenverfahren)
Eine Differenzengleichung ist eine numerisch lösbare rekursive Berechnungsvorschrift für eine diskret definierte Folge von nummerierten Folgeelementen bzw. Stützstellen im Abstand eines meist konstanten Intervalls oder bei zeitabhängigen Systemen .
Differenzengleichungen werden zur numerischen Berechnung in vielen wissenschaftlichen Disziplinen – wie Wirtschaft, Medizin, Technik, Elektrotechnik, Regelungstechnik, Kybernetik, Informatik, Akustik und andere – eingesetzt.
Eine Differenzengleichung steht in enger Beziehung zu einer Differentialgleichung. Die Differenzengleichung entsteht z. B., wenn der Differenzialquotient einer zu berechnenden Differenzialgleichung durch einen Differenzenquotient ausgetauscht wird. Durch diesen Vorgang entsteht automatisch das rekursive Verhalten der Differenzengleichung, bei der sich je nach Ordnung jedes aktuelle Folgeelement sich auf ein oder mehrere zurückliegende Folgeelemente bezieht.
Grundlagen der Differenzengleichungen
In der numerischen Mathematik werden zur Behandlung und Lösung von meist gewöhnlichen Differenzialgleichungen die kontinuierlichen Funktionswerte in Abhängigkeit von konstanten Intervallen hintereinander berechnet. Eine Differenzengleichung (auch Rekursionsgleichung genannt) ist eine Gleichung, die anstelle eines Differenzialquotienten einen Differenzenquotienten enthält. Sie ist von n-ter Ordnung, wenn die höchste Ordnung der vorkommenden Differenzen gleich ist.
Die nachfolgende Beschreibung des Artikels bezieht sich auf das Einschrittverfahren zur Lösung von gewöhnlichen Differenzialgleichungen 1. und 2. Ordnung und den Differenzialgleichungen dynamischer Systeme mit den Ein- und Ausgangsfolgen in Abhängigkeit von der Zeit.
Zu den bekanntesten einfachsten Einschrittverfahren bei Differenzengleichungen gehört des explizite Eulerverfahren zur numerischen Lösung von Anfangswertproblemen.
siehe auch Explizites Euler-Verfahren
siehe auch Implizites Euler-Verfahren
siehe auch Lineare Differenzengleichung
- Folgen
- Bei einer Differenzengleichung handelt es sich um eine rekursive Folge von nummerierten Elementen, also um eine Aufzählung von Zahlen. Rekursiv bedeutet in der Mathematik: jedes Folgeelement bezieht sich bei einer Differenzengleichung 1. Ordnung auf das zurückliegende Folgeelement.
- Eine Differenzengleichungen höherer Ordnung verknüpft die Werte der Ausgangsfolgen an zwei, drei oder mehreren zurückliegenden Zeitpunkten:
- .
- Je nach Art der Differenzialgleichung und der zugehörigen Differenzengleichung erhalten die Eingangs- und Ausgangsfolgeglieder der Differenzengleichung für die Nummerierung die Indizierung .
- Numerische Lösung:
- Die numerische Lösung einer Differenzengleichung erfolgt rekursiv über viele Berechnungsfolgen und stellt sich meist als eine tabellarisch geordnete Aufstellung von System-Ausgangsfolgen (Stützstellen, Knoten) in Abhängigkeit der Bezugsgröße dar.
- Bei dynamischen Systemen besteht die Abhängigkeit der Ausgangsgröße von der Eingangsfolge und dem Zeitschritt . Die Eingangsfolge hat keine rekursive Beziehung zu einem zurückliegendem Folgeglied .
- Schrittweite :
- Im Gegensatz zu einem kontinuierlichen Signalverlauf ist bei einem zeitdiskreten Signal die Größe der Signalinformation nur zu bestimmten Zeitpunkten definiert. Die Differenz von 2 benachbarten Zeitpunkten wird als Schrittweite definiert.
- Die Anzahl der Folgeglieder ist bei zeitabhängigen Systemen durch den gewünschten Darstellungszeitraum und die Genauigkeit der Approximation an die analytische Funktion durch die gewünschte Schrittweite der Folgeglieder bestimmt. Je kleiner ist, umso größer ist die Genauigkeit der Berechnung.
- Die Lösung der Differenzengleichung stellt sich als eine tabellarische Folge mit allen relevanten Größen wie die Folge k, zunehmende diskrete Zeit: , Ausgangsfolge , Eingangsfolge dar.
- Die Tabellengröße (Zeilen) wird bestimmt durch die Anzahl der Folgeglieder. Es gilt die Beziehung:
- ist der Darstellungszeitraum, Schrittzeit.
- Variablen:
- Einfache gewöhnliche Differenzialgleichungen haben als abhängige Variable die Größe und als unabhängige Variable die Größe .
- Bei Differenzialgleichungen von dynamischen Systemen bzw. gewöhnlichen Differenzialgleichungen mit konstanten Koeffizienten werden die physikalischen Größen als Ausgangsvariable , die Eingangsvariable und die unabhängige Variable definiert.
Definitionen der Ein- und Ausgangsfolgen:
- ist ein nummeriertes Element (Folgeglied) der rekursiven Ausgangsfolge des Systems mit . Jedes rekursive Folgeglied einer Differenzengleichung 1. Ordnung bezieht sich auf ein zurückliegendes Folgeglied .
- ist ein nummeriertes Element der Eingangsfolge des Systems mit . Die Eingangsfolge ist nicht rekursiv, sie kann z. B. eine normierte Sprungfunktion für alle Eingangsfolgen sein, oder die Ausgangsfolge eines anderen vorgeschalteten dynamischen Systems oder eine Tabelle sein.
- entspricht dem nächsten beliebig nummerierten Folgeglied nach einem Rechenschritt .
- entspricht einem zurückliegenden beliebig nummeriertem Folgeglied vor einem Rechenschritt .
Einfache Differenzengleichungen mit einer Ausgangsvariablen in Abhängigkeit von der Zeit
Für einfache numerische Berechnungen wie Zinseszins, Bevölkerungswachstum, Flüssigkeit in Behältern entleeren / füllen, liegen keine Differenzialgleichungen vor. Für diese Aufgaben müssen die rekursiven Folgeglieder von einem Anfangswert ausgehend für die unabhängige Variable , der Anzahl der Folgeglieder , der Zeitschrittweite , bestimmt werden. Sie enthält die Wertefolgen einer Variablen zu steigenden oder fallenden Zeitpunkten. Aus jedem zurückliegenden Folgeglied wird das nächste Folgeglied errechnet.
Dabei wird bei den Folgegliedern unterschieden:
- Bei der arithmetischen Folge wächst oder fällt jedes Folgeglied um einen festen Betrag. (Beispiel: Sparschwein)
- Bei der exponentiellen Folge wächst oder fällt jedes Folgeglied um einen relativen Anteil. (Beispiel: Zinseszins)
Für einen derartigen Typ Differenzengleichung lässt sich der Wert einer beliebigen Folge direkt algebraisch aus dem Anfangswert berechnen.
Die zugehörige Gleichung als Folge mit dem Verlauf einer Exponentialfunktion mit im Exponenten lautet:
Dabei ist eine Konstante und die Schrittweite.
Sie entspricht auch der Formel zur Berechnung von Zinseszins:
- Kapital
Der Wachstumsfaktor für eine steigende Funktion einer Folge lautet:
Beispiel einer Differenzengleichung zur numerischen Berechnung des Bevölkerungswachstums
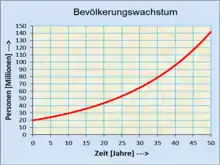
|
Gegeben:
Gesucht:
Differenzengleichung:
Entwicklung der Folgeglieder durch Differenzengleichungen oder durch Exponentialdarstellung:
Für diese Differenzengleichung kann für jede Folge auch die exponentielle Form benutzt werden:
|
Anmerkung: Ein mit dieser linearen Differenzengleichung berechnetes ungebremstes Wachstum wird es in der Praxis nicht geben, weil andere Einflüsse wie z. B. Nahrungsmittelknappheit dagegen wirken.
Anfangswertproblem
Die Lösung einer gewöhnlichen Differenzialgleichung 1. Ordnung ergibt in der Regel eine allgemeine Lösung in Form einer Funktionenschar mit unendlich vielen Lösungen mit ähnlichem Verhalten. Die Lösung eines Anfangswertproblems ist die Lösung der Differentialgleichung unter zusätzlicher Berücksichtigung eines Anfangswertes. Kennt man den Anfangszustand der Differenzialgleichung mit dem Anfangswert der unabhängigen Variablen für , ergibt sich die spezielle Lösung der Differenzialgleichung.
Bei gewöhnlichen Differenzialgleichungen kann durch Integration die Stammfunktion mit der Integrationskonstante C gebildet werden. Stammfunktion und Integrationskonstante müssen für eine exakte Lösung errechnet werden. Andere Methoden zur Lösung des Anfangswertproblems beschreiben eine Funktionenschar multiplikativ mit dem Scharparameter C.[1][2]
- In vielen Anwendungsfällen findet sich keine geschlossene Lösung der Differenzialgleichung, man ist daher auf numerische Verfahren angewiesen.
- Der Anfangswert für wird für die Lösung des Anfangswertproblems immer vorgegeben.
Als historisch einfachstes Verfahren zur Herleitung der Differenzengleichungen wird meistens das explizite Euler-Streckenzugverfahren genannt.[3][4]
Wird die Ableitung einer gewöhnlichen Differenzialgleichung durch den Vorwärts-Differenzenquotienten ersetzt,
entsteht die explizite Differenzengleichung .
Allgemeine Form der Differenzengleichung 1. O. nach dem Vorwärts-Differenzenquotienten (entspricht: "Euler-Vorwärts"):
Je kleiner die Schrittweite ist, umso geringer sind die Integrationsfehler. Andere Verfahren z. B. das Trapezverfahren von Heun oder das Runge-Kutta-Verfahren ermöglichen eine größere Schrittweite bei gleicher Genauigkeit.
Berechnungsbeispiel für das numerische Lösen einer linearen Differenzialgleichung 1. Ordnung
Differenzialgleichung: ergibt nach der Integration:[5]
- Analytische Lösung vorgegeben: .
- Anfangswert gewählt.
- Als Schrittweite wird: gewählt.
- Gesucht: Differenzengleichung mit Vorwärts-Differenzenquotient, Entwicklung der Folgeglieder.
- Entwicklung: Differenzengleichung durch Austausch Differentialquotient gegen Differenzenquotient:
- Differenzengleichung:
Gerechnet wurde mit der Tabellenkalkulation mit 15-Dezimalstellen-Genauigkeit,
für
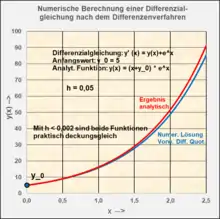
Entwicklung der Folgeglieder der Differenzengleichung:
| k | Differenzengleichung | Analytische Funktion | |
|---|---|---|---|
| 0 | 0 | Anfangswert | |
| 1 | |||
| 2 | |||
| 3 | |||
| 4 | |||
| 50 |
Fallschirmspringer
Die nichtlineare Bewegungsgleichung für den Fall mit Luftwiderstand lautet:
Daten:[6]
| Reibungskoeffizient: | Masse: | Erdbeschleunigung: | Schrittweite: |
| c = 0,32 kg/m | m = 80 kg | g = 10 m/s² | 1 s und 0,01 s |
Gesucht: Differenzengleichung, Geschwindigkeit der Masse .
Differenzengleichung (Vorwärtsdifferenzenquotient):
- , Anfangswert:
Entwicklung der Folgeglieder der Differenzengleichung bei einer Schrittweite von 1 s:
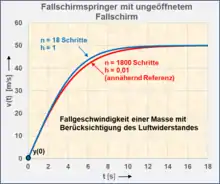
| k | Zeit [s] | Fallgeschwindigkeit |
|---|---|---|
| 0 | 0 | |
| 1 | 1 | = 10 |
| 2 | 2 | |
| 3 | 3 | |
| 18 | 18 |
Die Ergebnisse der Folgegleichungen ergeben Stützstellen mit asymptotischem Verlauf. Die Fallgeschwindigkeit nimmt ab nicht mehr zu. Die Fallstrecke nach der Fallzeit 13 s beträgt etwa 478 m (mit h = 0,01 s gerechnet).
Mathematisches Pendel
Mit dem zweiten Newtonschen Gesetz lässt sich die Bewegungsgleichung eines mathematischen Pendels für den Auslenkungswinkel herleiten:
- ,
mit Erdbeschleunigung und Pendellänge.
Diese Differentialgleichung 2. Ordnung wird nach der höchsten Ableitung aufgelöst:
- .
Durch die Substitution wird die Differentialgleichung zweiter Ordnung in ein System von 2 Differentialgleichungen erster Ordnung umgewandelt:
- ,
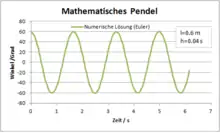
aus der wie folgt Differenzengleichungen abgeleitet werden. Die erste Differentialgleichung für die Winkelgeschwindigkeit kann mit dem expliziten Eulerverfahren integriert werden:
- Anfangswert:
Bei der Integration der zweiten Differentialgleichung kann die zuvor berechnete Winkelgeschwindigkeit verwendet werden (Euler rückwärts) was die Genauigkeit erheblich verbessert. Bei der nochmaligen Anwendung des expliziten Euler-Verfahrens würde sich eine aufklingende (instabile) Lösung ergeben.
- Anfangswert:
Das folgende Skript zeigt die Berechnung in gnuplot:
set print 'osz.dat'
h=0.04
l=0.6
x=0
omega=0; phi=60*pi/180
print x, omega, phi
do for [k=1:100] {
x=k*h
# Integration
omega=omega-9.81/l*sin(phi)*h
phi=phi+omega*h
print x, omega, phi*180/pi
}
unset print
plot 'osz.dat' using 1:3 title "Numerische Lösung"
…
Differenzenverfahren für die Bildung von Differenzengleichungen über Differenzenquotienten
Gewöhnliche lineare Differenzialgleichungen, die z. B. ein dynamisches System 1. Ordnung wie:
beschreiben, können nach dem Differenzenverfahren relativ einfach in eine Differenzengleichung überführt werden. Dies geschieht dadurch, dass die Differenzialquotienten der Differenzialgleichung direkt durch die verschiedenen Formen der Differenzenquotienten ausgetauscht werden. Damit entsteht automatisch die rekursive Differenzengleichung.[7]
Der Vorwärts-Differenzenquotient einer Differenzengleichung mit der Schrittweite lautet:
Für differenzierende Systeme bezieht sich der Differenzenquotient auf das Eingangssignal :
Rückwärts-Differenzenquotient einer Differenzengleichung:
Für differenzierende Systeme bezieht sich der Differenzenquotient auf das Eingangssignal .
Zentraler Differenzenquotient einer Differenzengleichung:
Wird der zentrale Differenzenquotient in eine Differenzialgleichung eingesetzt, handelt es sich nicht um einen arithmetischen Mittelwert zweier Verfahren. Die hohe Genauigkeit der Annäherung an eine analytische Funktion steigt nicht mit fallendem Wert von , sondern mit dem Quadrat des fallenden Wertes von .
Besonderheit: Die angenäherte diskrete Lösung der Differenzengleichung verläuft nicht unterhalb oder oberhalb der analytischen Funktion. Sie „schlängelt“ sich im Abstand von um die analytische Funktion.
Differenzialgleichungen und Differenzengleichungen dynamischer Systeme G(s)
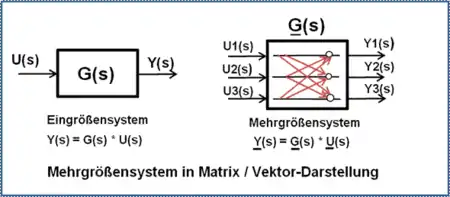
Lineare dynamische Systeme werden meist als Übertragungsfunktion beschrieben. Sie gelten für den für "Ruhezustand" des Systems mit dem Anfangswert Null und haben einen hohen Bekanntheitsgrad.
Lineare inhomogene Differenzialgleichungen können bei linearen dynamischen Systemen aus der Übertragungsfunktion G(s) mit Hilfe der inversen Laplace-Transformation ermittelt werden. Sie enthalten die abhängigen Variablen und . Die unabhängige Variable ist die Zeit .
Laut der Systemtheorie existieren nur 6 verschiedene Formen von phasenminimalen Übertragungsfunktionen , die einfach oder mehrfach bei dynamischen Systemen vorkommen können. Durch die inverse Laplace-Transformation ergeben sich mit Hilfe des Laplace-Differentiationssatzes Differenzialgleichungen 1. und 2. Ordnung als phasenminimale Elementarsysteme.
Ein Totzeitglied ist ein in der Praxis häufig vorkommendes lineares Übertragungsglied. Es entsteht durch Laufzeiten von Material oder Signalen. Die zugehörige Laplace-Transformierte ist keine gebrochene rationale Funktion, wie bei allen anderen linearen Übertragungsgliedern. Es ist aber numerisch leicht zu behandeln.
Tabelle wichtiger regulärer (phasenminimaler) Übertragungsfunktionen in Zeitkonstanten-Darstellung:
| Benennung | I-Glied Integration | (ideales) D-Glied Differentiation | (ideales) PD1-Glied Proportional-Differential | PT1-Glied Verzögerung | PT2kk-Glied Verzög. 2.Ord. konj. kompl. | Totzeitglied |
|---|---|---|---|---|---|---|
| Differenzialgleichung | *) |
*) | Differenzialgleichung existiert nicht | |||
| Übertragungsfunktion |
||||||
| Sprungantwort (Übergangsfunktion) |
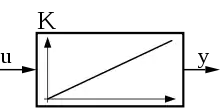 |  |  | 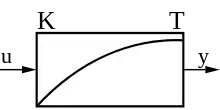 | 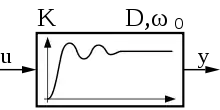 | 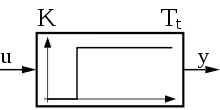 |
Es handelt sich hier nicht um eine Differenzialgleichung, sondern um eine Funktionsgleichung mit einer Ableitung des Eingangssignals. Diese Funktionsgleichungen entstehen durch die inverse Laplace-Transformation der zugehörigen Übertragungsfunktionen G(s).
Die Übertragungsfunktionen funktionsmäßig hintereinander geschalteter Systeme kompensieren sich bei gleichen Parametern vollständig zum Faktor 1, wenn z. B. ein Verzögerungsglied PT1-Glied mit einem "idealen" PD1-Glied hintereinander geschaltet sind. Das gleiche Verhalten muss auch für alle Folgeglieder der Differenzengleichungen gelten.
Ideales Element: Beim D-Glied und PD-Glied gilt für ein System, dessen Übertragungsfunktion im Zähler eine höhere Ordnung als im Nenner aufweist (Nullstellenüberschuss), als Hardware (ohne Verzögerungselement) nicht realisierbar. Ideale D- und PD-Glieder lassen sich mit Differenzengleichungen vortrefflich berechnen.
Die 6. Form des dynamischen Systems wurde nicht dargestellt, weil unbedeutend.
Herleitung von Differenzengleichungen für lineare dynamische Systeme
Die Differenzengleichungen 1. Ordnung nach den Verfahren des Vorwärts-Differenzenquotienten und des Rückwärts-Differenzenquotienten unterscheiden sich in der tabellarischen Anordnung nur durch eine Berechnungsfolge.[8]
Beim Verfahren nach dem Vorwärts-Differenzenquotienten stehen nur die Ausgangsvariablen und zur Verfügung. Gesucht wird die Differenzengleichung nach .
Beim Verfahren nach dem Rückwärts-Differenzenquotienten stehen nur die Ausgangsvariablen und zur Verfügung. Gesucht wird die Differenzengleichung nach .
Bei dem Vorwärts-Verfahren wird für und dem 1. Folgeglied ein Anfangswert zugeordnet. Erst das zweite Folgeglied mit und alle weiteren Folgeglieder werden aus der Differenzengleichung rekursiv berechnet.
Das Rückwärtsverfahren berechnet mit der betreffenden Differenzengleichung ab und alle Folgeglieder des dynamischen Systems. Entsprechend dem rekursiven Verfahren erhöht oder vermindert sich jedes Folgeglied für einen Zeitschritt um einen konstanten Betrag in Abhängigkeit von den Systemparametern. Dies bedeutet, dass das 1. Folgeglied bei bereits einen kleinen Wert, je nach Größe von erhält, obwohl der Anfangswert des Systems den Wert z. B. Null haben sollte.
Mit der nachfolgenden Aufstellung der Differenzengleichungen der Übertragungsglieder G(s) erster Ordnung lassen sich alle linearen Systeme höherer Ordnung zerlegen. Nach der Nullstellenanalyse von DGL höherer Ordnung entstehen unabhängige Systeme 1. O. und bei Systemen mit konjugiert komplexen Nullstellen unabhängige Systeme 2. Ordnung. Mit der Anwendung von Zustandsvariablen können alle DGL höherer Ordnung in gekoppelte DGL 1. Ordnung überführt werden.
Differenzengleichungen lassen sich mit jeder Programmiersprache einschließlich Tabellenkalkulation anwenden.
Das Ergebnis ist eine tabellarisch gespeicherte Folge von Berechnungswerten (Stützstellen) der Ausgangs- und Eingangsfolgen sowie der Zeit eines Systems 1. Ordnung im zeitlichen Abstand . Ebenso können mehrere hintereinander wirkende dynamische Systeme berechnet werden, wobei die Ausgangsfolgen eines Systems die Eingangsfolgen des nachgeschalteten Systems bedeuten.
- Beispiel der Herleitung einer Differenzengleichung für ein PT1-Glied mit dem Vorwärts-Differenzenquotienten:
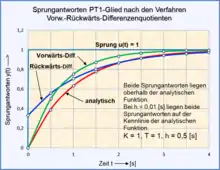
- Der Differenzialquotient der Differenzialgleichung des PT1-Gliedes wird durch den Differenzenquotient ersetzt mit folgendem Ansatz:
- Diese Gleichung wird nach aufgelöst.
- Die Differenzengleichung des PT1-Gliedes lautet mit dem Vorwärts-Differenzenquotienten:
- Die analytische Lösung des PT1-Gliedes lautet:
- Beispiel der Herleitung einer Differenzengleichung für ein PT1-Glied mit dem Rückwärts-Differenzenquotienten:[9]
- Der Differenzialquotient der Differenzialgleichung des PT1-Gliedes wird durch den Differenzenquotient ersetzt mit folgendem Ansatz:
- Diese Gleichung wird nach aufgelöst.
- Die Differenzengleichung des PT1-Gliedes lautet mit dem Rückwärts-Differenzenquotienten:
- Differenzengleichung des PT1-Gliedes in vereinfachter Schreibweise mit identischer mathematischer Funktion:
- Beispiel der Herleitung einer Differenzengleichung für ein differenzierendes Element wie das D-Glied oder PD1-Glied:
- Diese einfachen Differenzengleichungen entstehen durch Austausch der Ableitung der zugehörigen Funktionsgleichung durch einen entsprechenden Differenzenquotienten.
- Beispiel: Differenzialgleichung PD1-Glied (Methode Vorwärts-Differenzenquotienten):
Tabelle Differenzengleichungen von Übertragungssystemen G(s) erster Ordnung nach dem Differenzenverfahren
| Elementar- systeme |
Übertragungs- funktion |
Differenzengleichung
Differenzenquotient Rückwärts |
Differenzengleichung
Differenzenquotient Vorwärts |
|---|---|---|---|
| P-Glied Proportional | |||
| I-Glied Integration | |||
| PT1-Glied Verzögerung | |||
| D-Glied Differentiation | |||
| PD1-Glied Propotional-Diff. |
(Mit = Verstärkungsfaktor, = aktuelle zeitdiskrete Ausgangsgröße, = vorherige Ausgangsgröße, = Zeitkonstante, = aktuelle zeitdiskrete Eingangsgröße)
Lineare dynamische Systeme mit der Übertragungsfunktion sind laut Definition der Systemtheorie auf den Anfangswert festgelegt. Damit ist das zeitliche Systemverhalten für gegebene Eingangssignale bzw. eindeutig bestimmt.
Die dargestellten beiden Arten der Differenzengleichungen erfüllen die Bedingung der vollständigen Kompensation (Aufhebung) von Folgegliedern von verzögernden Systemen mit differenzierenden Systemen (z. B. PD1-Glied kompensiert PT1-Glied).
Tabellarische Definition der Folgeglieder von Differenzengleichungen am Beispiel der numerischen Integration
- Die Folgebezeichnungen , , sind relative Begriffe der Nummerierung. Sie haben erst eine absolute Bedeutung, wenn die Folge des ersten Folgegliedes der Differenzengleichung mit der Ausgangsgröße zugeordnet wird.
- Von den beiden Verfahren der Bildung von Differenzengleichungen nach den Vorwärts-Differenzenquotienten und dem Rückwärts-Differenzenquotienten ist das Verfahren nach dem Rückwärts-Differenzenquotienten vorzuziehen.
- Das Verfahren Rückwärts-Diff. ist bei einer geringeren Anzahl der Folgeglieder stabiler und genauer.
- Die Berechnung mit mehreren hintereinander wirkenden dynamischen Systemen mit Differenzengleichungen hat Rückwärts-Diff. eindeutige Vorteile der Genauigkeit gegenüber Vorwärts-Diff., weil Anfangswerte mit zu zeitlichen Verzögerungen führen.
- Differenzengleichungen nach dem Verfahren des Rückwärts-Diff. können auch mit einem Anfangswert starten, wenn die Eingangserregung bei ist und für weitere Folgen ist.
- Einfache Differenzialgleichungen ohne Eingangserregung vom Typ: starten bei beiden Verfahren von einem Anfangswert bei .
Differenzengleichung nach dem Vorwärts-Differenzenquotient für 3 Wertefolgen:
- Beispiel Differenzialgleichung (Funktionsgleichung) der Integration 1. Ordnung: ; .
| Spalte A - | Spalte B Folge k | Spalte C Zeitfolge t | Spalte D Signal | Spalte E Differenzengleichung |
|---|---|---|---|---|
| Zeile 50 | 0 | = Anfangswert | ||
| Zeile 51 | 1 | |||
| Zeile 52 | 2 |
- Anmerkung zur Tabelle: Werden die Eingangssignale in der Integrationsfunktion (Vorwärts-Differenzenquotient) anstatt nun (Spalte E) verwendet, ergibt sich ein verbessertes Rechenergebnis für . Dieser Vorteil reduziert sich linear mit kleiner werdendem .
Differenzengleichung nach dem Rückwärts-Differenzenquotient für 3 Wertefolgen:
- Beispiel Differenzialgleichung (Funktionsgleichung) der Integration 1. O.: .
| Spalte A - | Spalte B Folge k | Spalte C Zeitfolge t | Spalte D Signal | Spalte E Differenzengleichung |
|---|---|---|---|---|
| Zeile 50 | 0 | |||
| Zeile 51 | 1 | |||
| Zeile 52 | 2 |
Differenzengleichung nach dem Rückwärts-Differenzenquotient mit Anfangswert für 3 Wertefolgen:
- Beispiel Differenzialgleichung (Funktionsgleichung) der Integration 1. O.: kann mit einem Anfangswert starten, wenn für die anderen Folgen gegeben ist.
| Spalte A - | Spalte B Folge k | Spalte C Zeitfolge t | Spalte D Signal | Spalte E Differenzengleichung |
|---|---|---|---|---|
| Zeile 50 | 0 | |||
| Zeile 51 | 1 | |||
| Zeile 52 | 2 |
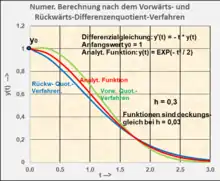
Beispiel einer Differenzengleichung nach dem Vorwärts- und Rückwärts-Differenzenquotienten ohne Eingangserregung:
- Beispiel Differenzialgleichung: Eingangssignal: .[10]
- Die zugehörigen Differenzengleichungen können mit einem Anfangswert starten.
- Differenzengleichung nach dem Vorwärts-Diff.: . .
- Differenzengleichung nach dem Rückwärts-Diff.: überführt in . .
Tabelle für das Beispiel Rückwärts-Differenzenquotient:
| Spalte A - | Spalte B Folge k | Spalte C Zeitfolge t | Spalte D Differenzengleichung |
|---|---|---|---|
| Zeile 50 | 0 | ||
| Zeile 51 | 1 | ||
| Zeile 52 | 2 |
Numerische Berechnung dynamischer Systeme mit Differenzialgleichungen zweiter und höherer Ordnung
Folgende Verfahren zur Lösung von dynamischen Systemen mit konjugiert komplexen Polen sind bekannt:
- Lösung einer DGL 2. O. mit einem Modellregelkreis
- Lösung einer DGL höherer Ordnung mit Differenzenquotienten
- Lösung einer DGL höherer Ordnung mit Zustandsvariablen
Lösung einer DGL 2. O. mit einem Modellregelkreis
Ein I-Glied und ein PT1-Glied werden zu einem Modellregelkreis geschaltet. Damit entsteht ein Schwingungsglied (), welches durch eine lineare DGL 2. O. mit konstanten Koeffizienten und einer Eingangserregung (Störfunktion) beschrieben wird:
Die Differenzengleichungen des I-Gliedes und des PT1-Gliedes erhalten die Koeffizienten aus den Zahlenwerten der vorgegebenen DGL 2. O. durch Faktorenvergleich.
Berechnet werden die drei Differenzengleichungen des I-Gliedes, des PT1-Gliedes und die Schließbedingung (Regelabweichung) des Modellregelkreises mit:
Diese Methode ist sehr einfach und genau hinsichtlich minimaler Anzahl der Folgeglieder. Sie bezieht aber nur auf die Lösung von DGL 2. O. und wird deshalb nicht weiter behandelt.
Lösung einer DGL höherer Ordnung mit Differenzenquotienten
Die Umwandlung einer Differenzialgleichung in eine Differenzengleichung erfordert für jede Ableitung einen entsprechenden Differenzenquotienten, die in vielen Publikationen definiert sind. Das nachfolgend dargestellte Berechnungsbeispiel eines -Gliedes 2. O. zeigt einen beträchtlichen algebraischen Aufwand.
Vorwärts-Differenzenquotient 2. Ordnung:
Rückwärts-Differenzenquotient 2. Ordnung:
Nach erfolgtem Einsetzen der Differenzenquotienten (hier Rückwärts-Differenzenquotient) anstelle der Differenzialquotienten der Differenzialgleichung eines dynamischen Systems 1. und 2. Ordnung lässt sich die so geschaffene Differenzengleichung lösen. Weil des Differenzenquotienten 2. Ordnung für und gesetzt wird, sind die Werte für und und damit kann für alle Folgen berechnet werden.
.png.webp)
Gegeben: Übertragungsfunktion im s-Bereich:
Gesucht: Differenzengleichung 2. Ordnung zur numerischen Bestimmung des System-Zeitverhaltens. Zugehörige Differentialgleichung nach dem Differentiationssatz der Laplace-Transformation: Die Differenzenquotienten werden in die nachfolgende Differenzengleichung eingesetzt: Die Brüche werden in einzelne additive Terme aufgelöst, um freistellen zu können, Hilfsgröße eingeführt:
Berechnungsbeispiel für einige Werte der Ausgangsfolge mit Sprung :
|
- Der Maximalwert der 1. Amplitude der Sprungantwort des Schwingungsgliedes erfolgt bei k = 78 und t = 0,78 [s] mit y(t) = 1,5192.
Lösung einer DGL höherer Ordnung mit Zustandsvariablen nach der Zustandsraumdarstellung
Ein Zustandsraummodell der Zustandsraumdarstellung symbolisiert die überführte Differenzialgleichung n-ter Ordnung in n-gekoppelte Zustands-Differenzialgleichungen erster Ordnung. Die Zustandsvariablen beschreiben physikalisch den Energiegehalt der in einem dynamischen System enthaltenen Speicherelemente.
Mit Hilfe des Signalflussplanes der Zustandsraumdarstellung#Regelungsnormalform lassen sich lineare gewöhnliche Differenzialgleichungen dynamischer Systeme höherer Ordnung einfach lösen. Dabei wird die gegebene DGL höherer Ordnung in verkoppelte DGL 1. Ordnung überführt. Die Differenzengleichung der Zustandsvariablen bestimmen die Lösung der DGL höherer Ordnung.
Die numerische Berechnung bezieht sich dabei auf den Signalflussplan der Regelungsnormalform des Zustandsraumes. Die systembeschreibende Differenzialgleichung wird in expliziter Darstellung (geordnet nach der höchsten Ableitung y(t)) in ein Signalflussdiagramm gebracht, wobei die Anzahl der Ableitungen von y(t) die Anzahl der Integratoren bestimmen.[11]
Die Regelungsnormalform ähnelt signaltechnisch der elektrischen Schaltung eines Analogrechners zur Lösung einer Differenzialgleichung, falls keine differentiellen Anteile des Übertragungssystems vorliegen. Sind Anfangswerte gegeben, werden die Integratoren direkt auf die Anfangswerte gesetzt, d. h. die tabellarisch geordneten Folgeglieder der numerischen Berechnung der Integratoren starten mit den Anfangswerten.
Dieser Signalflussplan der Regelungsnormalform lässt sich numerisch leicht berechnen. Für jede Ableitung der Differenzialgleichung muss numerisch eine Differenzengleichung der Integration (I-Glied) mit den zugehörigen Koeffizienten berechnet werden. Anfangswerte können sehr einfach berücksichtigt werden.
Laut Signalflussplan der Regelungsnormalform kann man die Darstellung einer Differenzialgleichung 2. Ordnung als einen zweischleifigen Kreis betrachten. Die Lösung der Differenzialgleichung entspricht für der Zustandsvariablen .
Laut Wirkungskreis des Signalflussplans werden drei numerisch lösbare Gleichungen benötigt:
- 1) Zustandsrückführung , 2) Integration von , 3) Integration von .
Da diese Gleichungen voneinander abhängig sind, können sie nicht zum gleichen Folgezeitpunkt berechnet werden. Zur Vermeidung von Zirkelbezug-Fehlermeldungen dürfen die beiden Differenzengleichungen der Integration nicht nur mit dem Verfahren des Rückwärts-Differenzenquotienten berechnet werden. Werden beide Integratoren mit dem Verfahren des Vorwärts-Differenzenquotienten berechnet, ergeben sich größere Abweichungen zur analytischen Funktion.
Bei zusammenhängenden Systemen bzw. Differenzengleichungen entspricht jede Ausgangsgröße einer Eingangsgröße der nachfolgenden Differenzengleichung.
Gegenüber dem Verfahren mit Differenzenquotienten 2. Ordnung ist das Verfahren nach der Regelungsnormalform durch geringere Anzahl der Folgeglieder bei gleicher Genauigkeit sehr überlegen.
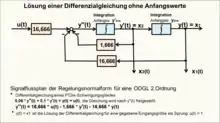
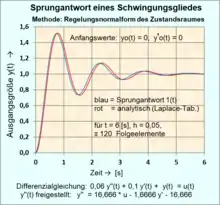
Berechnungsbeispiel einer DGL 2. O. mit Zustandsvariablen:
Gegeben: Übertragungsfunktion im s-Bereich:
Gesucht: Explizite Form der Differenzialgleichung 2. O. und Bestimmung des System-Zeitverhaltens .
Tabellarische Berechnung für einige Werte der Ausgangsfolge mit ; Sprung :
|
- Der Maximalwert der 1. Amplitude der Sprungantwort des Schwingungsgliedes erfolgt bei Zeile F65, k = 15 und t = 0,75 [s] mit = 1,515.
Anmerkung:
Laut Fachliteratur Ist es üblich, die Differenzengleichungen der Integration z. B. des gegebenen Beispiels der Differenzialgleichung 2. O. in zwei Zustandsgleichungen zusammenzufassen.
- und .
Ausgehend von einer DGL höherer Ordnung erzeugt man über Zustandsgrößen ein äquivalentes Differenzialgleichungssystem.[12]
Die im Beispiel angegebene Gleichung der Zustandsrückführung wird in die Zustandsgleichung der Integration x2 eingebracht. Die numerischen Gleichungen dafür lauten:
Anfangswert Anfangswert
Differenzengleichungssysteme
In der Technik kommen dynamische Systeme selten als einzelne Systeme vor, sondern es liegen verschiedenartige Systeme mit linearem, nichtlinearem oder unstetigem Systemverhalten vor, die in Reihe oder parallel oder mit Rückführungen zusammen wirken. Auf konventionellem Wege lassen sich solche Gesamtsysteme nicht mehr berechnen. Mittels Differenzengleichungen und logischen z. B. IF-THEN-ELSE-Anweisungen oder Tabellen, die die statische Nichtlinearität beschreiben, lassen sich solche Gesamtsysteme simulieren.
Kompensation von linearen dynamischen Systemen 1. Ordnung mit verzögerndem Verhalten
In der Praxis können mehrere hintereinander liegende dynamische Systeme als Verzögerungsglieder auftreten, die zu einer höheren Systemordnung führen und evtl. die Berechnung bzw. die Simulation erschweren. Mit Übertragungsfunktionen kann man mathematisch nachweisen, dass z. B. hintereinander wirkende PT1-Glieder durch (ideale) PD1-Glieder und I-Glieder durch (ideale) D-Glieder bei gleichen Faktoren und Zeitkonstanten sich vollständig zum Faktor 1 kompensieren. Das gleiche Verhalten erreicht man auch in der numerischen Berechnung dynamischer Systeme, wobei die Folgeglieder der verschiedenen Systeme sich vollständig kompensieren. Die Ausgangsfolgen eines dynamischen Systems werden zu Eingangsfolgen des nachfolgenden Systems.
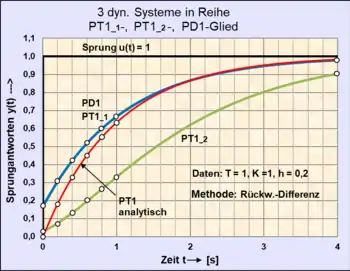
- Tabelle zur Darstellung numerischer Eingangs-/Ausgangsfolgen von hintereinander wirkenden zwei PT1-Gliedern und einem PD1-Glied zur Kompensation.
- Gewähltes Verfahren: Austausch Differenzialquotient der Differenzialgleichung durch Rückwärts-Differenzenquotient.
- Mit den gemeinsamen Daten: wird:
- -Glied:
- -Glied:
| Folge k | Zeit- schritt | Eingangs- folge | -Glied Folge | -Glied Folge | PD1-Glied Folge | PT1-Glied analytisch |
|---|---|---|---|---|---|---|
| 0 | 0 | 1 | 0,1667 | 0,0278 | 0,1667 | 0,0 |
| 1 | 0,2 | 1 | 0,3056 | 0,0741 | 0,3056 | 0,1813 |
| 2 | 0,4 | 1 | 0,4213 | 0,1319 | 0,4213 | 0,3297 |
| 3 | 0,6 | 1 | 0,5177 | 0,1962 | 0,5177 | 0,4512 |
| 4 | 0,8 | 1 | 0,5981 | 0,2632 | 0,5981 | 0,5507 |
| 5 | 1,0 | 1 | 0,6651 | 0,3302 | 0,6651 | 0,6321 |
| 20 | 4,0 | 1 | 0,9783 | 0,9022 | 0,9783 | 0,9817 |
- Ergebnis: Das -Glied wurde vollständig durch das ideale PD1-Glied kompensiert.
Liegen mehrere Verzögerungssysteme oder integrierende Systeme hintereinander, dann eignen sich die Differenzengleichungen nach dem Berechnungsverfahren mit dem Rückwärts-Differenzenquotienten vorteilhafter, weil für und das zugehörige Folgeglied immer ist.
Bei der Berechnung von z. B. 3 hintereinander liegenden Verzögerungsgliedern nach dem Berechnungsverfahren mit dem Vorwärts-Differenzenquotienten startet erst das 3. Verzögerungsglied bei , weil .
Simulationsmodell eines dynamischen Übertragungssystems
Mit der Simulation eines mathematischen Modells eines Übertragungssystems bzw. eines Regelkreises ergibt sich die Möglichkeit, mit geeigneten Testsignalen eine Systemanalyse oder eine Systemoptimierung durchzuführen.
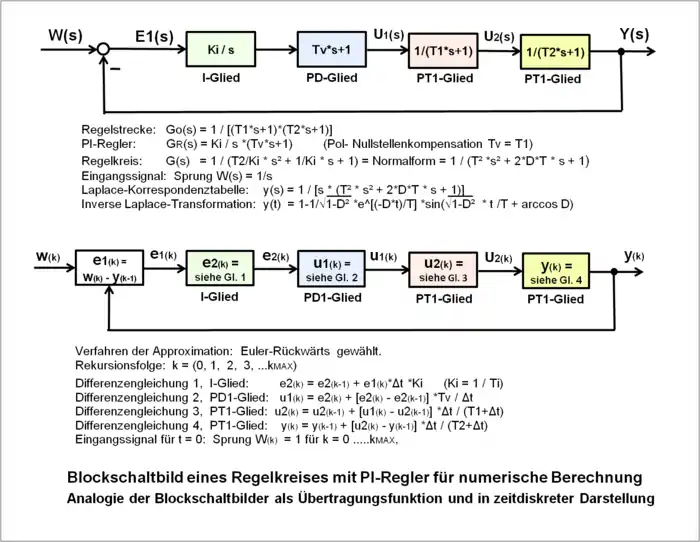
Der Vorteil der Simulation an einem Modell liegt auf der Hand. Es werden keine technischen Anlagen gefährdet, bzw. benötigt, der Zeitfaktor spielt keine Rolle, es können sehr schnelle oder sehr langsame Prozesse optimiert werden. Voraussetzung ist die mathematische Beschreibung eines gut angenäherten Modells der meist technischen Regelstrecke.
Das Modell (Modellbildung) eines Übertragungssystems ist das mathematische Abbild einer meist technischen (evtl. physikalischen, chemischen, biologischen) Einrichtung. Es wird analytisch über Differenzialgleichungen gewonnen oder experimentell durch Identifizierungsverfahren.
Die Modellierung einer bestehenden Hardware-Steuerstrecke oder Regelstrecke im Zeitbereich geschieht experimentell in der einfachsten Form durch eine grafische Aufzeichnung der Sprungantwort mit anschließender Analyse des zeitlichen Verhaltens. (Siehe Experimentelle Systemidentifikation)
Die Modellierung im Frequenzbereich geschieht durch Anregung des Systems durch eine variable Frequenz und Aufzeichnung der Ausgangsamplitude und Phase. Über den Frequenzgang wird die Übertragungsfunktion des Systems gebildet.
Nichtlineare Systeme können nicht durch Übertragungsfunktionen beschrieben werden. Durch zeitdiskrete Beschreibungen in Form logischer Befehle (z. B. bei Signalbegrenzungen) oder durch eine Tabelle bei einer nichtlinearen Kennlinie ist das relativ einfach möglich.
Testsignale
Den nichtperiodischen (deterministischen) Testsignalen kommt in der Systemtheorie eine zentrale Bedeutung zu. Mit ihrer Hilfe ist es möglich, ein Übertragungssystem zu testen, auf Stabilität zu prüfen oder Eigenschaften zu ermitteln. Den meist normierten Testsignalen ist gemeinsam, dass sie zum Zeitpunkt beginnen und bei einen Wert aufweisen. Für die numerische Berechnung werden die Eingangsfolgen der Sprungfunktion, der Impulsfunktion oder der Anstiegsfunktion verwendet.
siehe Regelstrecke#Testsignale
Vor- und Nachteile des numerischen Differenzenverfahrens
- Die numerische Berechnung von Differenzialgleichungen bzw. dynamischen Systemen erfordert gegenüber der konventionellen Lösung relativ geringe mathematische Kenntnisse.
- Die Differenzengleichung kann direkt über Differenzenquotienten aus der Differenzialgleichung gebildet werden.
- Der Approximationsfehler an eine analytische Funktion nach dem Vorwärts- oder Rückwärtsdifferenzenverfahren fällt linear mit fallender Schrittweite .
- Erfahrungswerte für die Darstellung asymptotischer Funktionsverläufe können je nach gewünschter Genauigkeit bei 100 bis 1000 Stützstellen liegen.
- Die numerische Berechnung schwingender Systeme mit Differenzialgleichungen 2. Ordnung erfordern eine sehr geringe Schrittweite bzw. eine hohe Anzahl von Folgegliedern zur Darstellung mehrerer Perioden. Es werden erheblich kleinere Schrittweiten benötigt, als bei der Darstellung asymptotischer Funktionen. So muss man beispielsweise für die Darstellung einer gedämpften Schwingungsfolge eine größere Anzahl von Stützstellen pro Schwingung zuordnen.
- Mit zunehmender Verringerung der Schrittweite und mit gegebenem Eingangssignal gleichen sich die die Funktionen beider Vorwärts-Rückwärts-Differenzenverfahren an.
- Die Berechnung von Differenzengleichungen nach Vorwärts- oder Rückwärts-Differenzenquotienten sind in Bezug auf die Genauigkeit praktisch identisch, kleine Schrittweite vorausgesetzt.
- Der Gesamtfehler einer numerischen Berechnung besteht aus dem Numerik-Verfahren und dem Rundungsfehler.
- Der Rundungsfehler muss berücksichtigt werden, wenn die Folgeglieder nicht mit ausreichender Stellengenauigkeit berechnet werden. Anderenfalls addieren sich die Rundungsfehler mit jedem Folgeglied.
- Laut einer Veröffentlichung (Thomas Westermann) wird in einem Vergleich mit dem Euler-Vorwärts-Verfahren (= Vorwärts-Differenzenquotient-Verfahren), dem Prädiktor-Korrektor-Verfahren und dem Runge-Kutta-Verfahren eine sinusförmige Spannung an einem Kondensator eines mit 220 V AC eingespeisten RC-Gliedes betrachtet. Eine durchgeführte Fehleranalyse ergab für eine Schrittweite von [s] gegenüber der Referenz für Euler-Vorwärts gegen Runge-Kutta einen etwa 12-fachen Wert des absoluten Fehlers.[13]
- Nachteilig bei dem numerischen Einschrittverfahren ist die große Zahl der Folgeelemente für die Berechnung mit hoher Genauigkeit.
Nichtlineare Übertragungssysteme
Lineare und nichtlineare DGL mit konstanten Koeffizienten sind mit Hilfe von Differenzengleichungen annäherungsweise (Approximation) leicht lösbar.
Im Gegensatz dazu sind relativ einfache Übertragungssystem-Strukturen mit nichtlinearen statischen Elementen durch konventionelle Rechenmethoden im kontinuierlichen Zeitbereich nicht mehr geschlossen lösbar.
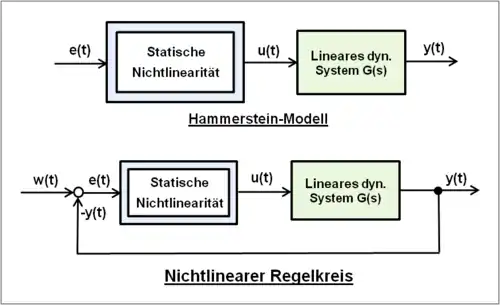
Nach dem Hammersteinmodell wird das nichtlineare Systemverhalten in ein statisches nichtlineares Modell in Verbindung als Reihenschaltung mit einem linearen dynamischen System betrachtet.
Maßnahmen zur Linearisierung nichtlinearer Übertragungssysteme:
- Begrenzungseffekte: Nachbildung der Begrenzung mit logischen Anweisungen,
- Nichtlineare Kennlinie: Anwendung eines Modellregelkreises zwingt zur Linearität,
- Nichtlinearität: durch logische Befehle wie logische Anweisungen z. B. IF-THEN-ELSE-Anweisungen oder Tabellen, die die statische Nichtlinearität beschreiben.
- Hysterese: Die nichtlineare Funktion wird in Tabellen gespeichert.
siehe auch Bild Regelungstechnik#Nichtlineares Übertragungssystem
Behandlung der Systemtotzeit (lineares System)
- Berechnung eines Annäherungsmodells mit Verzögerungen höherer Ordnung oder Allpassglieder,
- Speicherung von Folgegliedern mit Zugriff auf zeitlich mit zurückliegende Folgeglieder.
- Bei Anwendung der Tabellenkalkulation: INDEX-Funktion
Einzelnachweise
- Fachbuch: Jürgen Koch / Martin Stämpfle: „Mathematik für das Ingenieurstudium“, Kapitel „Gewöhnliche Differenzialgleichungen“, "Anfangswertproblem".
- Fachbuch:Thomas Westermann: Mathematik für Ingenieure, Ein anwendungsorientiertes Lehrbuch, Kapitel „Gewöhnliche Differenzialgleichungen“, "Anfangswertproblem".
- Prof. Dr. Bastian von Harrach, Goethe-Universität Frankfurt a. M., Skript „Numerik von Differenzialgleichungen“: Anfangswertproblem, Richtungsfeld, Euler-Verfahren (Kapitl 1.2.3, Seite 22), Runge-Kutta-Verfahren, Mehrschritt-Verfahren.
- Prof. Dr. Wandinger: Anfangswertprobleme 1. Ordnung. (PDF) S. 7.1-9, abgerufen am 7. September 2021..
- Die Darstellung des im Artikel benutzten Beispiels der Differenzialgleichung und der Gleichung der analytischen Funktion für stammt aus dem Skript und dem gleichnamigen Fachbuch von Prof. Dr. Thomas Westermann, Uni Karlsruhe, „Mathematik für Ingenieure, Anwendungsorientiertes Lehrbuch“, Kapitel „Numerisches Lösen“, 8. Auflage 2020.
- H. Biner, H.P. Dreyer, W. Hartmann, A. Moretti: Der Fallschirmspringer. Hrsg.: U. Kirchgraber. ETH Eidgenössische Technische Hochschule Zürich, 1993, S. 4–7 (Bericht No. 93-04 [PDF; abgerufen am 28. Dezember 2021]).
- Autor: Jürgen Dankert; Fachbuchreihe: Numerische Methoden der Mechanik, Einzelfachbuch: „Das Differenzenverfahren“, Springer Vieweg, Berlin, Auszug-Übersicht „Der Grundgedanke des Verfahrens besteht darin, die Differenzialquotienten in Differenzialgleichungen und Randbedingungen durch Differenzenquotienten zu ersetzen.“
- Prof. Dr. Christian Clemen, HS-Augsburg; Skript: Mathematik II, Kapitel: Numerische Differentiation, Numerische Integration, Numerische Lösung von gewöhnlichen Differenzialgleichungen, die Methoden von Euler, Heun und Runge-Kutta, verbesserte Euler-Verfahren.
- Prof. Dipl.-Ing. Manfred Ottens, FH Berlin, Skript „Grundlagen der Systemtheorie“, siehe „Kontinuierliche und zeitdiskrete Signale und Systeme“ und „Ausgangsfolge des zeitdiskreten Verzögerungsgliedes“. Vergleiche numerische Sprungantwort des PT1-Gliedes, Methode Rückwärts-Differenzenquotient, Seite 150.
- Grafik in Übereinstimmung mit dem Fachbuch: Bilen Emek Abali / Celal Cakiroglu: Numerische Methoden für Ingenieure, Springer Vieweg, Ausgabe 2020, Kapitel: „Verfahren zur Lösung gewöhnlicher Differentialgleichungen“.
- Holger Lutz, Wolfgang Wendt: Taschenbuch der Regelungstechnik mit MATLAB und Simulink. 12. Auflage. Verlag Europa-Lehrmittel, 2021, ISBN 978-3-8085-5870-6. Siehe Kapitel: "Normalformen von Übertragungssystemen"
- Fachbuch: Jürgen Koch, Martin Stämpfle: Mathematik für das Ingenieurstudium, Carl Hanser-Verlag München, Kapitel: „Euler-Verfahren für Differenzialgleichungssysteme“ und „Zustandsvariablen“.
- Buchauszug: Thomas Westermann: Mathematik für Ingenieure, Springerverlag, Google-Aufruf: „kap 19.pdf Mathematik für Ingenierure“. Anmerkung: Ist nicht in dem gleichnamigen Fachbuch: Thomas Westermann: Mathematik für Ingenieure, Springerverlag 8. Auflage, enthalten.
Literatur
- Andreas Meister / Thomas Sonar: Numerik „Eine lebendige und gut verständliche Einführung mit vielen Beispielen“, 1. Auflage 2018, Springer Spektrum, Springer-Verlag Deutschland, ISBN 978-3-662-58357-9.
- Bilen Emek Abali / Celal Cakiroglu: Numerische Methoden für Ingenieure, mit Anwendungsbeispielen in Python, Springer Vieweg, Ausgabe 2020, ISBN 978-3-662-61324-5.
- Jürgen Koch / Martin Stämpfle: Mathematik für das Ingenieurstudium 4. Auflage 2018, Carl Hanser Verlag München, ISBN 978-3-446-45166-7
- Berg, L.: Differenzengleichungen zweiter Ordnung mit Anwendungen. Darmstadt: Steinkopff, 1980.
- Berg, L.: Lineare Gleichungssysteme mit Bandstruktur. München, Wien: Hanser, 1986.
- Krause, U., und Nesemann, T.: Differenzengleichungen und diskrete dynamische Systeme. Stuttgart, Leipzig: Teubner, 1999.
- Franz Pfuff: Mathematik für Wirtschaftswissenschaftler kompakt. Vieweg+Teubner; Auflage: 1 (26. Februar 2009), ISBN 3-8348-0711-7, Kapitel 1, Abschnitt § 7 Differenzengleichungen und Finanzmathematik
- Dürr, R., und Ziegenbalg, J.: Mathematik für Computeranwendungen. Paderborn: Schöningh, 1989.
Weblinks
- 13. Differenzengleichungen – Kapitel über Differenzengleichungen mit mathematischen Beispielen, Uni Greifswald (pdf; 52 kB)