Implizites Euler-Verfahren

Das implizite Euler-Verfahren (nach Leonhard Euler) (auch Rückwärts-Euler-Verfahren) ist ein numerisches Verfahren zur Lösung von Anfangswertproblemen. Es ist ein implizites Verfahren, das heißt, in jedem Schritt muss eine – im Allgemeinen nichtlineare – Gleichung gelöst werden.

Das Verfahren

Zur numerischen Lösung des Anfangswertproblems:

{\dot {x}}=f(t,x),\quad \quad x(t_{0})=x_{0}

für eine gewöhnliche Differentialgleichung wähle man eine Diskretisierungsschrittweite $h>0$ , betrachte die diskreten Zeitpunkte

t_{k}=t_{0}+kh,\quad \quad k=0,1,2,\dots

und berechne die iterierten Werte[1]

x_{k+1}=x_{k}+hf(t_{k+1},x_{k+1})\quad ,\quad k=0,1,\dots

Der Wert $f(t_{k+1},x_{k+1})$ ist hierbei nicht explizit gegeben, sondern nur implizit, denn $x_{k+1}$ taucht auf beiden Seiten der Gleichung auf. Zur Berechnung von $x_{k+1}$ muss die Gleichung also in jedem Iterationsschritt gelöst werden, z. B. numerisch mit dem Newton-Verfahren. Dieses Problem stellt sich bei linearen Systemen nicht, da nach $x_{k+1}$ aufgelöst werden kann.

Die Werte $x_{k}$ stellen dann Approximationen an die tatsächlichen Werte $x(t_{k})$ der exakten Lösung des Anfangswertproblems dar. Je kleiner die Schrittweite $h$ gewählt wird, desto mehr Rechenarbeit muss geleistet werden, aber desto besser werden auch die approximierten Werte.

Wird ein Verfahren über $x_{k+1}=x_{k}+hf(t_{k},x_{k})$ definiert, erhält man das explizite Euler-Verfahren.

Eigenschaften

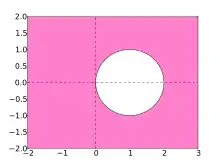
Stabilitätsgebiet des impliziten Euler-Verfahren.

Das implizite Euler-Verfahren hat Konsistenz- und Konvergenzordnung 1. Es ist A-stabil, sein Stabilitätsgebiet enthält also die komplette linke Halbebene der komplexen Zahlenebene. Es gibt damit für das implizite Euler-Verfahren keine Einschränkungen an die Zeitschritte aufgrund von Stabilitätseinschränkungen, was den Zwang des Lösens von Gleichungssystemen in jedem Schritt wettmacht. Aufgrund der geringen Ordnung ist es damit besonders für Probleme interessant, bei denen die Iteration in einen stabilen Endzustand hineinläuft und die Genauigkeit der Zwischenergebnisse nicht interessant ist.

Literatur

E. Hairer, S.P. Norsett, G. Wanner: Solving Ordinary Differential Equations I, Springer Verlag
M. Hermann: Numerik gewöhnlicher Differentialgleichungen, Anfangs- und Randwertprobleme, Oldenbourg Verlag, München und Wien, 2004, ISBN 3-486-27606-9

Einzelnachweise

Martin Hermann: Anfangswertprobleme und lineare Randwertprobleme. 2. Auflage. DE GRUYTER, 2017, ISBN 978-3-11-050036-3, S. 16–17 (eingeschränkte Vorschau in der Google-Buchsuche).

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Martin Hermann: Anfangswertprobleme und lineare Randwertprobleme. 2. Auflage. DE GRUYTER, 2017, ISBN 978-3-11-050036-3, S. 16–17 (eingeschränkte Vorschau in der Google-Buchsuche).