Diamantstruktur
Die Diamantstruktur (auch Diamantgitter, A4-Typ oder Diamanttyp) ist eine Kristallstruktur, das heißt das Anordnungsmuster der Atome eines kristallinen Materials. Entdeckt wurde dieser Strukturtyp beim Diamanten, einer Modifikation des Kohlenstoffs, aber auch weitere Materialien mit Atomen aus der 4. Hauptgruppe (vierwertige Elemente) können in dieser Struktur kristallisieren, beispielsweise Silicium, Germanium und Silicium-Germanium-Legierungen sowie α-Zinn.[1] Analog zum kristallinen Diamanten können auch niedermolekulare Verbindungen des Kohlenstoffs die Diamantstruktur aufweisen, sogenannte Diamantoide. Ihr einfachster Vertreter ist das Adamantan.[2]
Aufbau

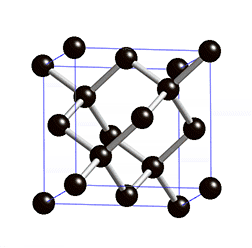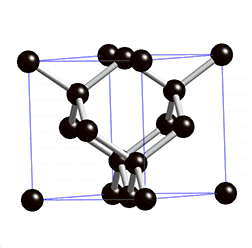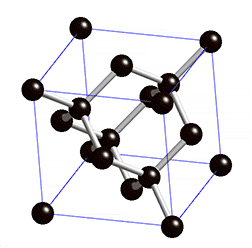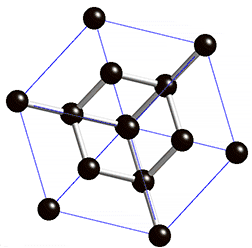
Die Diamantstruktur besteht aus einem kubisch-flächenzentrierten Gitter und der Basis {(0,0,0), (1/4,1/4,1/4)}. Anschaulich kann man die Diamantstruktur auch als Kombination zweier ineinander gestellter kubisch-flächenzentrierter Gitter beschreiben, die um 1/4 der Raumdiagonale gegeneinander verschoben sind.[3]
Jedes Kohlenstoffatom ist gleichwertig mit vier Nachbaratomen kovalent gebunden. Die Diamantstruktur entspricht damit der Zinkblende-Struktur (ZnS) mit dem Unterschied, dass die beiden kristallographischen Lagen (0,0,0) und (1/4,1/4,1/4) in der Zinkblende-Struktur von zwei verschiedenen Ionen besetzt sind. In beiden Strukturen ist jedes Atom mit 4 Atomen des gleichen Elements (beim Diamant C-Atome) verbunden. Der Grund dafür ist die Hybridisierung der Atomorbitale der äußersten Schale des Grundzustandes (Kohlenstoff: 1s22s22p2) zu vier sp3-Hybridorbitalen (1s2 2[sp3]4). Diese vier Orbitale sind aufgrund der elektromagnetischen Abstoßung mit größtmöglichem Abstand bzw. Winkel (109°28´) zueinander symmetrisch im Raum orientiert, sie zeigen in die Ecken eines gedachten Tetraeders.[4]
Vereinfachende zweidimensionale Abbildungen von Gittern mit vierwertigen Elementen zeigen ein gewöhnliches zweidimensionales Gittermuster. Im dreidimensionalen Raum nehmen die vier Valenzelektronen jedoch eine Position ein, die den vier Ecken eines Tetraeders entspricht, wobei der Atomkern im Mittelpunkt des Tetraeders liegt. In 2D-Darstellungen der 3D-Struktur von Diamanten wird das Atom gezeichnet, von dem aus sich die vier Ecken des Tetraeders in vier Bindungen (Valenzen) ausstrecken.
Bei Aufsicht auf diese Tetraeder der Diamantstruktur liegen drei Valenzen an den drei Ecken eines gleichseitigen Dreiecks und berühren drei benachbarte Atome, die in einer gemeinsamen Ebene liegen. Die vierte Valenz liegt in der Mitte des Dreiecks und berührt ein viertes benachbartes Atom in einer anderen Ebene – näher zum Betrachter hin bzw. weiter vom Betrachter weg. In der Diamantstruktur sind die Tetraeder abwechselnd so gedreht, dass die vierte Valenz zum Betrachter zeigt bzw. von ihm weg.
Symmetrie
Die Diamantstruktur hat die Raumgruppe Fd3m (Raumgruppen-Nr. 227).[5][6] Es handelt sich also um eine kubische Kristallstruktur.
Fd3m (Nr. 227) ist die gekürzte Schreibweise von F41/d 3 2/m. F bedeutet, dass das Bravais-Gitter flächenzentriert ist, 41/d bedeutet eine 41-Schraubenachse parallel der kristallographischen a-Achse (Drehung um 90° und Verschiebung (Translation) um 1/4 in Richtung der a-Achse), die 41-Schraubenachse steht weiterhin senkrecht auf einer „Diamantgleitspiegelebene“[7] (d). Entlang der Raumdiagonalen der Elementarzelle befinden sich dreizählige Drehinversionsachsen 3. Parallel zu den Diagonalen der Flächen der Elementarzelle befinden sich zweizählige Drehachsen (2) und senkrecht dazu Spiegelebenen (m). (Siehe dazu auch: Hermann-Mauguin-Symbol)
Eigenschaften
Wie erwähnt kristallisieren die typischen vierwertigen Halbleiter wie Silicium und Germanium in der Diamantstruktur. Durch die starken kovalenten Bindungen existieren keine freien Elektronen und die Materialien weisen bei T = 0 K (Temperatur am absoluten Nullpunkt) abgesättigte Valenzen, d. h. vollbesetzte Valenzbänder (VB), auf. Das Leitungsband (LB) ist hingegen völlig leer. Reine Halbleiter ohne Kristallbaufehler sind daher bei T = 0 K Isolatoren, denn es stehen keine Ladungsträger (Elektronen oder Defektelektronen) für den Stromtransport zur Verfügung.
Die Bandstruktur von Materialien mit Diamantstruktur weist meist eine Energielücke (indirekte Bandlücke) auf. Diese nimmt je nach Element unterschiedliche Werte an (bei 300 K: Eg,Diamant = 5,33 eV, Eg,Silicium = 1,14 eV, Eg,Germanium= 0,67 eV, Eg,Zinn= 0,08 eV). Bei den geringen Werten für die Energielücke bei Silicium, Germanium und Zinn reicht bereits die Wärmeenergie bei Raumtemperatur aus, um Elektronen aus dem Valenzband in das Leitungsband zu heben.[8] Die Elektronen im LB und die zurückbleibenden Defektelektronen im VB können nun unter dem Einfluss eines von außen angelegten elektrischen Feldes den elektrischen Strom leiten. Dieser Übergang der Elektronen vom Valenzband zum Leitungsband kann auch durch Photonen verursacht werden (photoelektrischer Effekt). Außerdem kann die Energielücke durch gezieltes Verunreinigen (Dotierung) und den damit entstehenden Haftstellen (ortsgebunden) verringert und somit die Leitfähigkeit erhöht werden (Störstellenleitung).
Da beim Diamant nur vier der acht tetraedischen Lücken von Kohlenstoffatomen besetzt sind, ist das Gitter relativ stark aufgeweitet. Die Packungsdichte der Diamantstruktur – nicht nur beim Diamant – ist somit vergleichsweise klein, nur etwa 34 Prozent des verfügbaren Volumens sind besetzt.[4]
Die besondere Härte von Diamant lässt sich mit dem Strukturmodell allein nicht erklären, sie ist eine Folge der besonders festen und gerichteten kovalenten Bindungen, die die tetraedischen sp3-Orbitale des Kohlenstoffs eingehen.[9]
Literatur
- Rudolf Gross, Achim Marx: Festkörperphysik. Oldenbourg Wissenschaftsverlag, 2012, ISBN 978-3486712940.
Weblinks
Einzelnachweise
- Rudolf Gross, Achim Marx: Festkörperphysik. Oldenbourg Verlag, 2012, ISBN 3-486-71294-2, S. 31 (eingeschränkte Vorschau in der Google-Buchsuche).
- Kurt Peter C. Vollhardt, Neil E. Schore: Organische Chemie. John Wiley & Sons, 2011, ISBN 3-527-32754-1, S. 168 (eingeschränkte Vorschau in der Google-Buchsuche).
- Charles Kittel: Einführung in die Festkörperphysik. Oldenbourg Verlag, 2013, ISBN 3-486-59755-8, S. 20 (eingeschränkte Vorschau in der Google-Buchsuche).
- Will Kleber, Hans-Joachim Bautsch, Joachim Bohm: Einführung in die Kristallographie - Will Kleber, Hans-Joachim Bautsch, Joachim Bohm. Oldenbourg Verlag, 2002, ISBN 3-486-59885-6, S. 157 (eingeschränkte Vorschau in der Google-Buchsuche).
- Koji Kobashi: Diamond films: chemical vapor deposition for oriented and heteroepitaxial growth. Elsevier, 2005, ISBN 978-0-08-044723-0, 2.1 Structure of diamond, S. 9.
- Text zu kubischem Diamant. Universität Konstanz. Abgerufen am 30. August 2011.
- Werner Massa: Kristallstrukturbestimmung. Springer DE, 2009, ISBN 3-8348-9593-8, S. 67 (eingeschränkte Vorschau in der Google-Buchsuche).
- Walter J. Moore: Grundlagen der Physikalischen Chemie. Walter de Gruyter, 1990, ISBN 3-11-009941-1, S. 744 (eingeschränkte Vorschau in der Google-Buchsuche).
- Horst Briehl: Chemie der Werkstoffe. Springer, 2007, ISBN 3-8351-0223-0, S. 29 (eingeschränkte Vorschau in der Google-Buchsuche).