0,999…

Die periodische Dezimalzahl 0,999… (auch mit mehr oder weniger Neunern vor den Auslassungspunkten geschrieben oder als 0,9 oder 0,(9)) bezeichnet die reelle Zahl 1. Die Symbole „0,999…“ und „1“ stellen also dieselbe Zahl dar (siehe Stellenwertnotation). Beweise dieser Gleichung wurden mit unterschiedlichem Grad an Strenge formuliert, je nach bevorzugter Einführung der reellen Zahlen, Hintergrundannahmen, historischem Kontext und Zielgruppe.

Künstlerische Darstellung der Dezimalzahl

Ferner hat jede abbrechende Dezimalzahl ungleich 0 eine alternative Darstellung mit unendlich vielen Neunern, zum Beispiel 8,31999… für 8,32. Die abbrechende Darstellung wird wegen der Kürze meist bevorzugt, was die Fehlannahme begünstigt, sie sei die einzige. Das gleiche Phänomen tritt auch in anderen Basen auf. Gleichwohl wurden Systeme entwickelt, in denen die Gleichung nicht gilt.

Dieser Artikel soll eine Übersicht geben, unter welchen mathematischen Regeln der Symbolfolge 0,999… welche mathematische Bedeutung gegeben werden kann.

Elementare Beweise

Die folgenden Beweise nutzen Konzepte, die aus der Schulmathematik bekannt sind. Dabei wird angenommen, dass periodische Dezimalbruchentwicklungen stets eine rationale Zahl darstellen. So wird etwa $1/3=0{,}333\dots$ als gegeben angenommen, da die handschriftliche Division dieses Resultat erzeugt. In den weiteren Betrachtungen geht es daher nicht darum, ob $0{,}999\dots$ etwas Sinnvolles darstellt, sondern nur noch um die Frage, welche Zahl damit gemeint sein soll. Die handschriftlichen Verfahren zur Durchführung der vier Grundrechenarten werden ebenfalls auf nichtabbrechende Dezimalbruchentwicklungen übertragen und als weiterhin gültig angenommen.

Schriftliche Subtraktion

Wird $0{,}999\dots$ schriftlich von links nach rechts von $1$ subtrahiert, ergibt sich $0{,}000\dots$

Brüche

Durch schriftliche Division lässt sich der Quotient 1/9 in die Dezimalzahl 0,111… umschreiben. Eine Multiplikation von 9 mal 1 macht jede Stelle zu einer 9, also ist 9 mal 0,111… gleich 0,999…, und 9 mal 1/9 ist gleich 1, woraus 0,999… = 1 folgt:

{\begin{aligned}0{,}333\ldots &{}={\frac {1}{3}}\\3\cdot 0{,}333\ldots &{}=3\cdot {\frac {1}{3}}\\0{,}999\ldots &{}=1\end{aligned}}

{\begin{aligned}0{,}111\ldots &{}={\frac {1}{9}}\\9\cdot 0{,}111\ldots &{}=9\cdot {\frac {1}{9}}\\0{,}999\ldots &{}=1\end{aligned}}

Der Beweis lässt sich auch mit anderen Brüchen führen wie 2/7 = 0,285714 285714 …: 285714/2 ist gleich 142857, dies mal 7 ergibt 999999. Meist werden sie aber mit den Brüchen 1/3 oder 1/9 geführt, da ihre Perioden einstellig sind und sie lediglich die Multiplikation mit einer einstelligen Zahl erfordern.

Umformung einer Unbestimmten

$x=0{,}999\ldots$ lässt sich wie folgt umarbeiten:

{\begin{aligned}x&=0{,}999\ldots \\10x&=9{,}999\ldots \\10x-x&=9{,}999\ldots -0{,}999\ldots \\9x&=9\\x&=1\end{aligned}}

Durchschnitt

Wären 0,999… und 1 verschiedene Zahlen, wäre der Durchschnitt (0,999… + 1)/2 = 1,999…/2 wieder ein anderer. Tatsächlich ist 1,999…/2 = 0,999…, womit bewiesen ist, dass 0,999… = 1 ist.

Stellenwertsysteme

Im Stellenwertsystem zur Basis q entspricht die (in der Standardnotation hingeschriebene) Zahl 0,999… dem Bruch 9/(q − 1). Für die Basis q = 10 gilt also:

0{,}999\ldots ={\frac {9}{10-1}}={\frac {9}{9}}=1

Diskussion

Die obigen Beweise fußen auf Annahmen, deren Sinn hinterfragt werden könnte, wenn sie als Axiome hingenommen werden.[1] Eine Alternative, die den Kernpunkt bei der dichten Ordnung der reellen Zahlen ansetzt:

Sollen reelle Zahlen durch Dezimaldarstellungen eingeführt werden, wird oft definiert, dass x kleiner als y ist, wenn die Dezimaldarstellungen der Zahlen verschieden sind und die von links aus gesehen erste unterschiedliche Stelle von x kleiner ist als die entsprechende Stelle von y. Zum Beispiel ist (0)43,23 kleiner als 123,25, weil der erste Unterschied bei 0 < 1 zu sehen ist. Nach dieser Definition kommt es auch tatsächlich zu dem Schluss 0,999… < 1.

An der Stelle sollte jedoch bedacht werden, dass von den reellen Zahlen eine dichte Ordnung verlangt wird: Zwischen zwei verschiedenen reellen Zahlen liegt stets eine von den beiden verschiedene dritte. Demzufolge ist es sinnvoll, zu definieren, dass x kleiner als y ist, wenn es nach dem bereits erwähnten Kriterium eine Zahl dazwischen gibt, und weil bei 0,999… alle Stellen mit 9 – der höchsten Ziffer – belegt sind, kann es keine Zahl zwischen 0,999… und 1 geben, womit 0,999… = 1 ist.[2]

Für einen tieferen Einblick lohnt sich ein Blick auf den analytischen Beweis.

Analytischer Beweis

Dezimalzahlen können als unendliche Reihen definiert werden. Im Allgemeinen:

d_{0}{,}d_{1}d_{2}d_{3}d_{4}\ldots =d_{0}+d_{1}\left({\tfrac {1}{10}}\right)+d_{2}\left({\tfrac {1}{10}}\right)^{2}+d_{3}\left({\tfrac {1}{10}}\right)^{3}+d_{4}\left({\tfrac {1}{10}}\right)^{4}+\cdots

Für den Fall 0,999… kann der Konvergenzsatz für geometrische Reihen angewandt werden:[3]

Wenn

|r|<1\,\!

, dann

ar+ar^{2}+ar^{3}+\cdots ={\frac {ar}{1-r}}

.

Da 0,999… eine geometrische Reihe mit a = 9 und r = 1/10 ist, gilt:

0{,}999\ldots =9\left({\tfrac {1}{10}}\right)+9\left({\tfrac {1}{10}}\right)^{2}+9\left({\tfrac {1}{10}}\right)^{3}+\cdots ={\frac {9\left({\tfrac {1}{10}}\right)}{1-{\tfrac {1}{10}}}}=1

Dieser Beweis (eigentlich, dass 10 = 9,999… ist) erscheint in Leonhard Eulers Vollständiger Anleitung zur Algebra.[4]

Eine typische Herleitung aus dem 18. Jahrhundert nutzte einen algebraischen Beweis ähnlich dem oberen. 1811 brachte John Bonnycastle in seinem Lehrbuch An Introduction to Algebra ein Argument mit der geometrischen Reihe.[5] Eine Reaktion des 19. Jahrhunderts gegen solch eine großzügige Summierung ergab eine Definition, die bis heute dominiert: Die Reihe aus den Gliedern einer unendlichen Folge ist definiert als der Grenzwert der Folge ihrer Partialsummen (Summen aus den ersten endlich vielen Summanden).

Eine Folge (a₀, a₁, a₂, …) hat den Grenzwert x, wenn es für alle $\varepsilon$ > 0 ein Glied der Folge gibt, ab dem alle Glieder weniger als $\varepsilon$ von x entfernt sind. 0,999… kann als Grenzwert der Folge (0,9, 0,99, 0,999, …) verstanden werden:[6]

0{,}999\ldots =\lim _{n\to \infty }0{,}\underbrace {99\ldots 9} _{n}=\lim _{n\to \infty }\sum _{k=1}^{n}{\frac {9}{10^{k}}}=\lim _{n\to \infty }\left(1-{\frac {1}{10^{n}}}\right)=1-\lim _{n\to \infty }{\frac {1}{10^{n}}}=1

Der letzte Schritt folgt aus der archimedischen Eigenschaft der reellen Zahlen. Die grenzwertbasierte Haltung findet sich auch in weniger präzisen Formulierungen. So erklärt das Lehrbuch The University Arithmetic aus dem Jahr 1846: „.999 +, continued to infinity = 1, because every annexation of a 9 brings the value closer to 1“ Arithmetic for Schools (1895) sagt: „when a large number of 9s is taken, the difference between 1 and .99999… becomes inconceivably small“[7]

Durch die Interpretation als Grenzwert kann auch Darstellungen wie 0,999…1 eine Bedeutung beigemessen werden. 0,999…1 wäre dann als Grenzwert von (0,1, 0,91, 0,991, …) aufzufassen, ist damit aber wieder gleich 1. Im Allgemeinen haben Stellen nach einer Periode keine Auswirkung.

Beweise durch die Konstruktion der reellen Zahlen

Einige Ansätze definieren die reellen Zahlen ausdrücklich als Strukturen, die sich aus den rationalen Zahlen ergeben, durch axiomatische Mengenlehre. Die natürlichen Zahlen – 0, 1, 2, 3 und so weiter – beginnen mit 0 und fahren aufwärts fort, sodass jede Zahl einen Nachfolger hat. Die natürlichen Zahlen können mit ihren Gegenzahlen erweitert werden, um die ganzen Zahlen zu erhalten, und weiter um die Verhältnisse zwischen den Zahlen, um die rationalen Zahlen zu erhalten. Diese Systeme werden von der Arithmetik der Addition, Subtraktion, Multiplikation und Division begleitet. Darüber hinaus haben sie eine Ordnung, sodass jede Zahl mit einer anderen verglichen werden kann und entweder kleiner, größer oder gleich ist.

Der Schritt von den rationalen Zahlen zu den reellen ist eine bedeutende Erweiterung. Es gibt mindestens drei bekannte Wege, sie zu bewerkstelligen: Dedekindsche Schnitte, Cauchy-Folgen (beide 1872 veröffentlicht) und Intervallschachtelungen. Beweise für 0,999… = 1, die solche Konstruktionen direkt nutzen, sind nicht in Lehrbüchern über Analysis zu finden. Selbst wenn eine Konstruktion angeboten wird, wird sie normalerweise verwendet, um die Axiome der reellen Zahlen zu beweisen, die dann den obigen Beweis stützen. Allerdings wurde mehrfach die Meinung geäußert, dass es logisch angemessener ist, mit einer Konstruktion zu starten.[8]

Dedekindsche Schnitte

Eine reelle Zahl kann als Dedekindscher Schnitt in $\mathbb {Q}$ definiert werden, also als vollständige Unterteilung der rationalen Zahlen in zwei nichtleere Mengen L|R, sodass l < r für alle l $\in$ L und r $\in$ R gilt.[9] Die linke Menge von 0,999… enthält genau die rationalen Zahlen r, für die r kleiner ist als 0,9… mit einer beliebigen Anzahl von endlich vielen Neunern, also kleiner als eine Zahl der Form:

1-\left({\frac {1}{10}}\right)^{n}

Da die Elemente der linken Menge alle rationalen Zahlen kleiner als 1 – so wie sie bei den rationalen Zahlen definiert ist – sind, wird der Schnitt 1 genannt.[10]

Die Definition der reellen Zahlen als Dedekindsche Schnitte wurde erstmals 1872 von Richard Dedekind veröffentlicht.[11]

Cauchy-Folgen

Eine Folge heißt Cauchy-Folge, wenn es für alle $\varepsilon$ > 0 ein Glied der Folge gibt, ab dem alle Glieder weniger als $\varepsilon$ voneinander entfernt sind. Um allen Cauchy-Folgen einen konkreten Grenzwert zuordnen zu können, werden die reellen Zahlen als Äquivalenzklassen von Cauchy-Folgen eingeführt. Zwei Cauchy-Folgen a und b heißen äquivalent, wenn die Folge (a_n − b_n) den Grenzwert 0 hat, also eine Nullfolge ist. Die Zahl 1 steht für die Äquivalenzklasse der Cauchy-Folge (1, 1, 1, …), 0,999… steht für die Äquivalenzklasse der Cauchy-Folge (0,9, 0,99, 0,999, …). Die Folgen sind äquivalent wegen:

\lim _{n\to \infty }\left(1-\sum _{k=1}^{n}{\frac {9}{10^{k}}}\right)=\lim _{n\to \infty }{\frac {1}{10^{n}}}=0

Ein möglicher Beweis dafür ist, dass alle Glieder ab dem n-ten weniger als $\varepsilon$ von 0 entfernt sind, wenn $\varepsilon$ = m/n ist. Damit ist 0,999… = 1.

Diese Definition der reellen Zahlen wurde erstmals 1872 unabhängig voneinander von Eduard Heine und Georg Cantor veröffentlicht.[11]

Intervallschachtelungen

Veranschaulichung der Gleichung 1 = 0,222…₃ mit Intervallschachtelungen

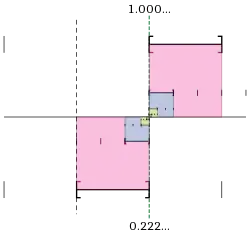
Die reellen Zahlen lassen sich ebenso als Äquivalenzklassen rationaler Intervallschachtelungen definieren. Eine Folge von Intervallen ([a_n, b_n]) heißt Intervallschachtelung, wenn a monoton wächst, b monoton fällt, a_n $\leq$ b_n für alle n gilt, und die Folge (b_n − a_n) eine Nullfolge ist. Zwei Intervallschachtelungen $([a_{n},b_{n}])$ und $([a'_{n},b'_{n}])$ sind äquivalent, wenn stets $a_{n}\leq b'_{n}$ und $a'_{n}\leq b_{n}$ gilt.

d₀,d₁d₂d₃… steht für die Äquivalenzklasse der Intervallschachtelung ([d₀, d₀ + 1], [d₀,d₁, d₀,d₁ + 0,1], …), folglich ist 0,999… die Äquivalenzklasse der Intervallschachtelung ([0, 1], [0,9, 1], [0,99, 1], …), 1 die der Intervallschachtelung ([1, 2], [1, 1,1], [1, 1,01], …). Da die geforderte Eigenschaft der Äquivalenz erfüllt ist, gilt 0,999… = 1.

Verallgemeinerungen

Die Tatsache, dass 0,999… = 1 ist, lässt sich auf verschiedene Arten verallgemeinern. Jede abbrechende Dezimalzahl ungleich 0 hat eine alternative Darstellung mit unendlich vielen Neunern, zum Beispiel 0,24999… für 0,25. Ein analoges Phänomen tritt in jeder Basis $q$ für die Ziffern mit Wert $q-1$ auf: So ist im Dualsystem 0,111… = 1, im Ternärsystem 0,222… = 1 und so weiter.

In nicht ganzzahligen Basen gibt es auch unterschiedliche Darstellungen. Mit dem Goldenen Schnitt φ = (1 + √5)/2 als Basis („Phinärsystem“) gibt es neben 1 und 0,101010… unendlich viele weitere Möglichkeiten, die Zahl Eins darzustellen. Im Allgemeinen gibt es für fast alle q zwischen 1 und 2 überabzählbar unendlich viele Basis-q-Darstellungen von 1. Auf der anderen Seite gibt es immer noch überabzählbar unendlich viele q (einschließlich aller natürlichen Zahlen größer als 1), für die es nur eine Basis-q-Darstellung für 1 außer der trivialen (1) gibt. 1998 bestimmten Vilmos Komornik und Paola Loreti die kleinste Basis mit dieser Eigenschaft, die Komornik-Loreti-Konstante 1,787231650… In dieser Basis ist 1 = 0,11010011001011010010110011010011…; die Stellen ergeben sich aus der Thue-Morse-Folge.[12]

Weitere Beispiele für unterschiedliche Darstellungen des gleichen Wertes sind:[13]

1/2 = 0,111… = 1,111… im balancierten Ternärsystem.
1 = 0,1234… im umgekehrten fakultätsbasierten Zahlensystem mit den Basen 2!, 3!, 4!, … für Nachkommastellen.

Harold B. Curtis weist auf ein anderes Kuriosum hin: 0,666… + 0,666…² = 1,111…

Anwendung

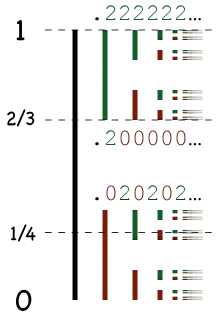
Positionen von 1/4, 2/3 und 1 in der Cantor-Menge

1802 veröffentlichte H. Goodwin eine Entdeckung über das Auftreten von Neunern in periodischen Dezimaldarstellungen von Brüchen mit bestimmten Primzahlen als Nenner. Beispiele sind:

1/7 = 0,142857142857… und 142 + 857 = 999.
1/73 = 0,0136986301369863… und 0136 + 9863 = 9999.

E. Midy bewies 1836 einen allgemeinen Satz über solche Brüche, der nun als der Satz von Midy bekannt ist: Hat die Periode des vollständig gekürzten Bruches a/p eine gerade Anzahl von Stellen und ist p prim, ist die Summe der beiden Hälften der Periode eine Folge von Neunern. Die Veröffentlichung war obskur und es ist unklar, ob der Beweis direkt 0,999… nutzte, doch zumindest ein moderner Beweis von W. G. Leavitt tut dies.

Die Cantor-Menge, welche entsteht, wenn aus dem Intervall [0, 1] der reellen Zahlen von 0 bis 1 unendlich oft das offene mittlere Drittel aus den verbleibenden Intervallen entfernt wird, lässt sich auch als Menge der reellen Zahlen aus [0, 1] beschreiben, die sich im Ternärsystem nur mit den Ziffern 0 und 2 darstellen lassen. Die n-te Nachkommastelle beschreibt dabei die Position des Punktes nach dem n-ten Schritt der Konstruktion. Die Zahl 1 könnte etwa als 0,222…₃ dargestellt werden, was andeutet, dass sie nach jedem Schritt rechts positioniert ist. 1/3 = 0,1₃ = 0,0222…₃ liegt nach der ersten Entfernung links, nach jeder weiteren rechts.[14] 1/4 = 0,020202…₃ liegt abwechselnd links und rechts.

Cantors zweites Diagonalargument verwendet ein Verfahren, das zu jeder Folge reeller Nachkommaanteile ein neues konstruiert, und zeigt somit die Überabzählbarkeit der reellen Zahlen: Es wird eine Zahl gebildet, deren n-te Nachkommastelle eine andere ist als die n-te Nachkommastelle des n-ten Folgenglieds. Ist die Wahl der Dezimaldarstellung beliebig, entsteht damit jedoch nicht notwendigerweise eine neue Zahl. Dies kann behoben werden, indem eine nicht abbrechende Darstellung der Zahlen gefordert und die Ersetzung einer Stelle durch 0 verboten wird.

Liangpan Li legte 2011 eine Konstruktion der reellen Zahlen dar, bei der 0,999… und 1 und Ähnliches als äquivalent definiert werden. Eine Vorzeichenfunktion wird beschrieben mit:

{\text{sign}}(x):={\begin{cases}0&\;{\text{wenn}}\;x\geq 0{,}000\ldots \\1&\;{\text{wenn}}\;x\leq (-1){,}999\ldots \\\end{cases}}

Skeptizismus

Die Gleichung 0,999… = 1 wird aus diversen Gründen angezweifelt:

Einige nehmen an, jede reelle Zahl hätte eine eindeutige Dezimaldarstellung.
Einige sehen in 0,999… eine unbestimmte endliche oder potentiell oder aktual unendliche Anzahl von Neunern, aber keine Einschränkung, weitere Dezimalstellen hinzuzufügen, um eine Zahl zwischen 0,999… und 1 zu bilden. 0,999…1 könnte als Beispiel genannt werden.
Einige interpretieren 0,999… als direkten Vorgänger von 1.
Einige sehen 0,999… als Folge statt Grenzwert.

Diese Ideen entsprechen nicht der üblichen dezimalen Notation in der (reellen) Arithmetik, können jedoch in alternativen Systemen gültig sein, die speziell für den Zweck oder für den allgemeinen mathematischen Nutzen entworfen wurden.

Denkbar ist auch, dass f(0,999…) als $\lim _{x\to 1}f(x)$ interpretiert wird, sodass zwar einerseits 0,999… = 1 akzeptiert wird, andererseits jedoch auch (0,999…² − 1)/(0,999… − 1) = 2, während (1² − 1)/(1 − 1) undefiniert ist. Dies so zu schreiben, ist jedoch nicht üblich und irreführend.

Bekanntheit

Mit dem Wachstum des Internets haben Debatten über 0,999… das Klassenzimmer verlassen und sind in Internetforen verbreitet, einschließlich solcher, die wenig mit Mathematik zu tun haben. Die Newsgroups de.sci.mathematik und sci.math haben die Frage in die FAQ aufgenommen.

Lina Elbers erhielt einen Preis von der Deutschen Mathematiker-Vereinigung für die klügste Frage, die Mathematikprofessoren gestellt wurde: Warum 0,999… nicht kleiner als 1 ist. Damals war sie Sechstklässlerin.[15]

Die Abfolge der sechs Neuner in der Kreiszahl $\pi$ ab der 762. Nachkommastelle ist als Feynman-Punkt bekannt und wurde nach Richard Feynman benannt, der einst sagte, er wolle die Zahl bis zu diesem Punkt lernen, sodass er sie bis zu der Stelle rezitieren und dann „und so weiter“ sagen kann, was suggeriert, die Zahl sei rational.

Ein Witz zu diesem Thema lautet:

Frage: Wie viele Mathematiker braucht man, um eine Glühbirne zu wechseln?

Antwort: 0,9

Andere Strukturen

Hyperreelle Zahlen

Der analytische Beweis für 0,999… = 1 beruht auf der archimedischen Eigenschaft. Diese besagt, dass es zu jedem $\varepsilon$ > 0 eine natürliche Zahl n gibt, sodass 1/n < $\varepsilon$ ist. Einige Systeme bieten allerdings noch kleinere Zahlen, sogenannte Infinitesimalzahlen.

Zum Beispiel enthalten die dualen Zahlen ein neues Element ε, das sich analog zu der imaginären Einheit i verhält, allerdings mit dem Unterschied ε² = 0 statt i² = −1. Jede duale Zahl hat die Form a + bε mit reellen a und b. Die resultierende Struktur ist für das automatische Differenzieren nützlich. Wird die lexikographische Ordnung durch a + bε < c + dε genau dann, wenn a < c oder sowohl a = c als auch b < d definiert, sind die Vielfachen von ε infinitesimal. Für die Dezimaldarstellung gelten aber die gleichen Konventionen, es gilt also immer noch 0,999… = 1.

Ein Unterschied kann mit den hyperreellen Zahlen ${}^{*}\mathbb {R}$ gemacht werden: Es handelt sich um eine Erweiterung der reellen Zahlen mit Zahlen, die größer sind als jede natürliche Zahl, bei der das Transferprinzip erfüllt ist: Jede Aussage in der Prädikatenlogik erster Stufe, die für $\mathbb {R}$ gilt, gilt auch für ${}^{*}\mathbb {R}$ . Während jede reelle Zahl aus dem Intervall [0, 1] durch eine Ziffernfolge

0,d₁d₂d₃…

mit natürlichen Zahlen als Indizes dargestellt werden kann, kann nach der Schreibweise von A. H. Lightstone jede hyperreelle Zahl aus dem Intervall [0, 1]* durch eine Hyperfolge

0,d₁d₂d₃…;…d_{ω − 1}d_ωd_{ω + 1}…

mit hypernatürlichen Zahlen als Indizes dargestellt werden.[16] Während Lightstone 0,999… nicht direkt erwähnte, zeigte er, dass 1/3 mit 0,333…;…333… dargestellt wird. Die Zahl 1 könnte somit mit 0,999…;…999… dargestellt werden. „0,333…;…000…“ und „0,999…;…000…“ entsprechen keiner hyperreellen Zahl, auf der anderen Seite lässt sich sagen, dass 0,999…;…999000…, deren letzte 9 von einer beliebigen hypernatürlichen Zahl indiziert wird, kleiner als 1 ist.

Zudem präsentierten Karin und Mikhail Katz eine Interpretation von 0,999… als hyperreelle Zahl:

{\underset {\omega }{0{,}\underbrace {999\ldots } }}\;=1\;-\;{\frac {1}{10^{\omega }}}

[17]

Ian Stewart charakterisiert diese Interpretation als einen vollkommen angemessenen Weg, die Intuition, dass in 0,999… „ein bisschen“ bis 1 fehlt, streng zu rechtfertigen.[18]

In der Ultrapotenzkonstruktion könnte 0,9 als die Äquivalenzklasse der Folge (0,9, 0,99, 0,999, …) interpretiert werden. Diese ist kleiner als 1 = (1, 1, 1, …). Neben Katz und Katz hinterfragt auch Robert Ely die Annahme, dass Ideen über 0,999… < 1 fehlerhafte Intuitionen über reelle Zahlen seien und sieht sie eher als Nichtstandard-Intuitionen, die bei dem Lernen von Analysis behilflich sein könnten.[19][20] José Benardete argumentiert in seinem Buch Infinity: An essay in metaphysics, dass einige natürliche vormathematische Intuitionen nicht ausgedrückt werden können, wenn eine Beschränkung auf ein allzu restriktives System vorliegt.

Hackenbush

Auch die kombinatorische Spieltheorie stellt Alternativen bereit. 1974 beschrieb Elwyn Berlekamp einen Zusammenhang zwischen unendlichen Positionen im blauroten Hackenbush und Binärzahlen. Zum Beispiel hat die Hackenbush-Position LRRLRLRL… den Wert 0,010101…₂ = 1/3. Der Wert von LRLLL… (0,111…₂) ist infinitesimal kleiner als 1. Der Unterschied ist die surreale Zahl 1/ω = 0,000…₂, die dem Hackenbush-String LRRRR… entspricht.

Im Allgemeinen stehen zwei verschiedene Binärzahlen stets für unterschiedliche Hackenbush-Positionen. So ist bei den reellen Zahlen 0,10111…₂ = 0,11000…₂ = 3/4. Nach Berlekamps Zuordnung ist die erste Zahl aber der Wert von LRLRLLL…, die zweite der Wert von LRLLRRR…

Überdenken der Subtraktion

Der Subtraktionsbeweis kann untergraben werden, wenn die Differenz 1 − 0,999… schlicht nicht existiert. Zu mathematischen Strukturen, in denen die Addition, aber nicht die Subtraktion abgeschlossen ist, gehören unter anderem einige kommutative Halbgruppen, kommutative Monoide und Halbringe. Fred Richman betrachtet zwei solcher Systeme, bei denen 0,999… < 1 ist.

Zunächst definiert Richman eine nicht negative Dezimalzahl als buchstäbliche Dezimaldarstellung. Er definiert die lexikographische Ordnung und eine Addition, womit 0,999… < 1 schlicht daher gilt, weil 0 < 1 ist, allerdings ist 0,999… + x = 1 + x für jedes nicht abbrechende x. Eine Besonderheit der Dezimalzahlen ist also, dass die Addition nicht immer gekürzt werden kann. Mit der Addition und Multiplikation bilden die Dezimalzahlen einen positiven total geordneten kommutativen Halbring.[21]

Dann definiert er ein anderes System, das er Schnitt D nennt und das den Dedekindschen Schnitten entspricht, allerdings mit dem Unterschied, dass er für einen Dezimalbruch d sowohl den Schnitt $(-\infty ,d)$ als auch den Schnitt $(-\infty ,d]$ zulässt. Das Ergebnis ist, dass die reellen Zahlen „unbehaglich mit den Dezimalbrüchen zusammenleben“. Es gibt keine positiven Infinitesimalzahlen im Schnitt D, aber eine Art negative Infinitesimalzahl, 0⁻, die keine Dezimaldarstellung besitzt. Er folgert, dass 0,999… = 1 + 0⁻, während die Gleichung 0,999… + x = 1 keine Lösung hat.[22]

p-adische Zahlen

Während 0,999… im Dezimalsystem eine erste 9 hat, aber keine letzte, hat bei den 10-adischen Zahlen …999 umgekehrt keine erste 9, wohl aber eine letzte. Wird 1 hinzuaddiert, entsteht eine Zahl …000 = 0, sodass …999 = −1 ist (jedenfalls, wenn wir uns in einer additiven Gruppe mit einer 0 und einer Erzeugenden 1 bewegen).[23] Eine andere „Herleitung“ nutzt die geometrische Reihe:

\ldots 999=9+9(10)+9(10)^{2}+9(10)^{3}+\cdots ={\frac {9}{1-10}}=-1.

Während die Reihe bei den reellen Zahlen nicht konvergiert (sie also keine reelle Zahl darstellt), konvergiert sie bei den 10-adischen Zahlen.[24] Auch besteht die Möglichkeit, hier den „Beweis“ mit der Multiplikation mit 10 anzuwenden:[23]

{\begin{aligned}x&=\ldots 999\\10x&=\ldots 990\\10x&=x-9\\x&=-1\end{aligned}}

Diese 10-adischen Zahlen bilden einen nicht-nullteilerfreien Ring, in dem die Nullteiler nichtabbrechende Darstellungen haben (s. Proendliche Zahl#10-adische Zahlen).

Schlussendlich könnte eine „Theorie“ der „Doppeldezimalzahlen“ betrachtet werden, die die reellen Zahlen mit den 10-adischen kombiniert, und in der …999,999… = 0 ist (aufgrund von …999 = −1, 0,999… = 1 und −1 + 1 = 0).[25]

Siehe auch

Literatur

K. T. Alligood, T. D. Sauer, J. A. Yorke: Chaos: An introduction to dynamical systems. Springer, 1996, ISBN 0-387-94677-2, 4.1 Cantor Sets.
Tom M. Apostol: Mathematical analysis. 2e Auflage. Addison-Wesley, 1974, ISBN 0-201-00288-4.
R. G. Bartle, D. R. Sherbert: Introduction to real analysis. Wiley, 1982, ISBN 0-471-05944-7.
Richard Beals: Analysis. Cambridge UP, 2004, ISBN 0-521-60047-2.
Elwyn R. Berlekamp, John H. Conway, Richard K. Guy: Winning Ways for your Mathematical Plays. Academic Press, 1982, ISBN 0-12-091101-9.
Martin Berz: Automatic differentiation as nonarchimedean analysis. Elsevier, 1992, S. 439–450.
Kim Beswick: Why Does 0.999... = 1?: A Perennial Question and Number Sense. In: Australian Mathematics Teacher. Band 60, Nr. 4, 2004, S. 7–9.
Bryan H. Bunch: Mathematical fallacies and paradoxes. Van Nostrand Reinhold, 1982, ISBN 0-442-24905-5.
Brian Burrell: Merriam-Webster’s Guide to Everyday Math: A Home and Business Reference. Merriam-Webster, 1998, ISBN 0-87779-621-1.
William Byers: How Mathematicians Think: Using Ambiguity, Contradiction, and Paradox to Create Mathematics. Princeton UP, 2007, ISBN 0-691-12738-7.
John B. Conway: Functions of one complex variable I. 2e Auflage. Springer-Verlag, 1978, ISBN 0-691-12738-7.
Charles Davies: The University Arithmetic: Embracing the Science of Numbers, and Their Numerous Applications. A.S. Barnes, 1846 (eingeschränkte Vorschau in der Google-Buchsuche).
Frank C. DeSua: A system isomorphic to the reals. In: The American Mathematical Monthly. Band 67, Nr. 9, November 1960, S. 900–903, doi:10.2307/2309468.
Ed Dubinsky, Kirk Weller, Michael McDonald, Anne Brown: Some historical issues and paradoxes regarding the concept of infinity: an APOS analysis: part 2. In: Educational Studies in Mathematics. Band 60, Nr. 2, 2005, S. 253–266, doi:10.1007/s10649-005-0473-0.
Barbara Edwards, Michael Ward: Surprises from mathematics education research: Student (mis)use of mathematical definitions. In: The American Mathematical Monthly. Band 111, Nr. 5, Mai 2004, S. 411–425, doi:10.2307/4145268.
Herbert B. Enderton: Elements of set theory. Elsevier, 1977, ISBN 0-12-238440-7.
Paul Fjelstad: The repeating integer paradox. In: The College Mathematics Journal. Band 26, Nr. 1, Januar 1995, S. 11–15, doi:10.2307/2687285.
Anthony Gardiner: Understanding Infinity: The Mathematics of Infinite Processes. Dover, 2003, ISBN 0-486-42538-X.
Timothy Gowers: Mathematics: A Very Short Introduction. Oxford UP, 2002, ISBN 0-19-285361-9.
Ivor Grattan-Guinness: The development of the foundations of mathematical analysis from Euler to Riemann. MIT Press, 1970, ISBN 0-262-07034-0.
H. B. Griffiths, P. J. Hilton: A Comprehensive Textbook of Classical Mathematics: A Contemporary Interpretation. Van Nostrand Reinhold, London 1970, ISBN 0-442-02863-6.
Karin Usadi Katz, Mikhail G. Katz: When is .999… less than 1? In: The Montana Mathematics Enthusiast. Band 7, Nr. 1, 2010, S. 3–30 (umt.edu).
A. J. Kempner: Anormal Systems of Numeration. In: The American Mathematical Monthly. Band 43, Nr. 10, Dezember 1936, S. 610–617, doi:10.2307/2300532.
Vilmos Komornik, Paola Loreti: Unique Developments in Non-Integer Bases. In: The American Mathematical Monthly. Band 105, Nr. 7, 1998, S. 636–639, doi:10.2307/2589246.
W. G. Leavitt: A Theorem on Repeating Decimals. In: The American Mathematical Monthly. Band 74, Nr. 6, 1967, S. 669–673, doi:10.2307/2314251.
W. G. Leavitt: Repeating Decimals. In: The College Mathematics Journal. Band 15, Nr. 4, September 1984, S. 299–308, doi:10.2307/2686394.
Albert H. Lightstone: Infinitesimals. In: The American Mathematical Monthly. Band 79, Nr. 3, März 1972, S. 242–251, doi:10.2307/2316619.
Richard Mankiewicz: The story of mathematics. Cassell, 2000, ISBN 0-304-35473-2.
Eli Maor: To infinity and beyond: a cultural history of the infinite. Birkhäuser, 1987, ISBN 3-7643-3325-1.
Joseph Mazur: Euclid in the Rainforest: Discovering Universal Truths in Logic and Math. Pearson: Pi Press, 2005, ISBN 0-13-147994-6.
James R. Munkres: Topology. 2e Auflage. Prentice-Hall, 2000, ISBN 0-13-181629-2.
Rafael Núñez: Do Real Numbers Really Move? Language, Thought, and Gesture: The Embodied Cognitive Foundations of Mathematics. In: 18 Unconventional Essays on the Nature of Mathematics. Springer, 2006, S. 160–181 (ucsd.edu).
George Pedrick: A First Course in Analysis. Springer, 1994, ISBN 0-387-94108-8.
Anthony Peressini, Dominic Peressini: Perspectives on Mathematical Practices. Hrsg.: Bart van Kerkhove, Jean Paul van Bendegem (= Logic, Epistemology, and the Unity of Science. Band 5). Springer, 2007, ISBN 978-1-4020-5033-6, Philosophy of Mathematics and Mathematics Education.
Marko Petkovšek: Ambiguous Numbers are Dense. In: American Mathematical Monthly. Band 97, Nr. 5, Mai 1990, S. 408–411, doi:10.2307/2324393.
Márcia Pinto, David Tall: Following students’ development in a traditional university analysis course. 14. Januar 2001 (warwick.ac.uk [PDF]).
M. H. Protter, Charles B. Morrey: A first course in real analysis. 2e Auflage. Springer, 1991, ISBN 0-387-97437-7.
Charles Chapman Pugh: Real mathematical analysis. Springer, 2001, ISBN 0-387-95297-7.
Paul Renteln, Allan Dundes: Foolproof: A Sampling of Mathematical Folk Humor. In: Notices of the AMS. Band 52, Nr. 1, Januar 2005, S. 24–34 (ams.org [PDF]).
Fred Richman: Is 0.999… = 1? In: Mathematics Magazine. Band 72, Nr. 5, Dezember 1999, S. 396–400.
Abraham Robinson: Non-standard analysis. Princeton University Press, 1996, ISBN 0-691-04490-2.
Maxwell Rosenlicht: Introduction to Analysis. Dover, 1985, ISBN 0-486-65038-3.
Walter Rudin: Principles of mathematical analysis. 3e Auflage. McGraw-Hill, 1976, ISBN 0-07-054235-X.
Maurice Shrader-Frechette: Complementary Rational Numbers. In: Mathematics Magazine. Band 51, Nr. 2, März 1978, S. 90–98, doi:10.2307/2690144.
Houshang Sohrab: Basic Real Analysis. Birkhäuser, 2003, ISBN 0-8176-4211-0.
M. Starbird, T. Starbird: Required Redundancy in the Representation of Reals. In: Proceedings of the American Mathematical Society. Band 114, Nr. 3, März 1992, S. 769–774, doi:10.1090/S0002-9939-1992-1086343-5.
Ian Stewart: The Foundations of Mathematics. Oxford UP, 1977, ISBN 0-19-853165-6.
Ian Stewart: Professor Stewart’s Hoard of Mathematical Treasures. Profile Books, 2009, ISBN 978-1-84668-292-6.
James Stewart: Calculus: Early transcendentals. 4. Auflage. Brooks/Cole, 1999, ISBN 0-534-36298-2.
D. O. Tall, R. L. E. Schwarzenberger: Conflicts in the Learning of Real Numbers and Limits. In: Mathematics Teaching. Band 82, 1978, S. 44–49 (warwick.ac.uk [PDF]).
David O. Tall: Conflicts and Catastrophes in the Learning of Mathematics. In: Mathematical Education for Teaching. Band 2, Nr. 4, 1977, S. 2–18 (warwick.ac.uk [PDF]).
David O. Tall: Cognitive Development In Advanced Mathematics Using Technology. In: Mathematics Education Research Journal. Band 12, Nr. 3, 2000, S. 210–230 (warwick.ac.uk [PDF]).
Dr. Hans von Mangoldt: Einführung in die höhere Mathematik. 1. Auflage. Verlag von S. Hirzel, Leipzig 1911, Reihenzahlen.
David F. Wallace: Everything and more: a compact history of infinity. Norton, 2003, ISBN 0-393-00338-8.
S. E. Burkov: One-dimensional model of the quasicrystalline alloy. In: Journal of Statistical Physics. Band 47, Nr. 3/4, 1987, S. 409, doi:10.1007/BF01007518.
Bob Burn: 81.15 A Case of Conflict. In: The Mathematical Gazette. Band 81, Nr. 490, März 1997, S. 109–112, doi:10.2307/3618786.
J. B. Calvert, E. R. Tuttle, Michael S. Martin, Peter Warren: The Age of Newton: An Intensive Interdisciplinary Course. In: The History Teacher. Band 14, Nr. 2, Februar 1981, S. 167–190, doi:10.2307/493261.
Younggi Choi, Jonghoon Do: Equality Involved in 0.999… and (-8)⅓. In: For the Learning of Mathematics. Band 25, Nr. 3, November 2005, S. 13–15.
K. Y. Choong, D. E. Daykin, C. R. Rathbone: Rational Approximations to π. In: Mathematics of Computation. Band 25, Nr. 114, April 1971, S. 387–392, doi:10.2307/2004936.
B. Edwards: Proceedings of the 19th Annual Meeting of the North American Chapter of the International Group for the Psychology of Mathematics Education. In: ERIC Clearinghouse for Science, Mathematics and Environmental Education. Band 1, 1997, An undergraduate student’s understanding and use of mathematical definitions in real analysis, S. 17–22.
Petr Eisenmann: Why is it not true that 0.999… < 1? In: The Teaching of Mathematics. Band 11, Nr. 1, 2008, S. 35–40.
Robert Ely: Nonstandard student conceptions about infinitesimals. In: Journal for Research in Mathematics Education. Band 41, Nr. 2, 2010, S. 117–146.
J. Ferrini-Mundy, K. Graham: Research issues in undergraduate mathematics learning. In: MAA Notes. Band 33, 1994, Research in calculus learning: Understanding of limits, derivatives and integrals, S. 31–45.
Joseph Lewittes: Midy’s Theorem for Periodic Decimals. In: MAA Notes. Band 33, 1994, arxiv:math.NT/0605182.
Karin Usadi Katz, Mikhail G. Katz: Zooming in on infinitesimal 1 − .9.. in a post-triumvirate era. In: MAA Notes. Band 33, 1994, arxiv:math.NT/0605182.
Tony Gardiner: Infinite processes in elementary mathematics: How much should we tell the children? In: The Mathematical Gazette. Band 69, Nr. 448, Juni 1985, S. 77–87, doi:10.2307/3616921.
John Monaghan: Real Mathematics: One Aspect of the Future of A-Level. In: The Mathematical Gazette. Band 72, Nr. 462, Dezember 1988, S. 276–281, doi:10.2307/3619940.
Maria Angeles Navarro, Pedro Pérez Carreras: A Socratic methodological proposal for the study of the equality 0.999…=1. In: The Teaching of Mathematics. Band 13, Nr. 1, 2010, S. 17–34 (sanu.ac.rs [PDF]).
Malgorzata Przenioslo: Images of the limit of function formed in the course of mathematical studies at the university. In: Educational Studies in Mathematics. Band 55, Nr. 1–3, März 2004, S. 103–132, doi:10.1023/B:EDUC.0000017667.70982.05.
James T. Sandefur: Using Self-Similarity to Find Length, Area, and Dimension. In: The American Mathematical Monthly. Band 103, Nr. 2, Februar 1996, S. 107–120, doi:10.2307/2975103.
Anna Sierpińska: Humanities students and epistemological obstacles related to limits. In: Educational Studies in Mathematics. Band 18, Nr. 4, November 1987, S. 371–396, doi:10.1007/BF00240986.
Jennifer Earles Szydlik: Mathematical Beliefs and Conceptual Understanding of the Limit of a Function. In: Journal for Research in Mathematics Education. Band 31, Nr. 3, Mai 2000, S. 258–276, doi:10.2307/749807.
David O. Tall: Dynamic mathematics and the blending of knowledge structures in the calculus. In: ZDM Mathematics Education. Band 41, Nr. 4, 2009, S. 481–492, doi:10.1007/s11858-009-0192-6.
David O. Tall: Intuitions of infinity. In: Mathematics in School. Band 10, Nr. 3, Mai 1981, S. 30–33.

Weblinks

.999999... = 1? bei cut-the-knot (englisch)
Beweis, dass 0,9999... nicht nur gerundet, sondern gleich 1 ist bei mathelounge
Unendliche Perioden Beispiel 164Y (0,9999... =1) bei mathepedia
1 = 0.999... in der Math Central (englisch)
Point nine recurring equals one bei Things Of Interest (englisch)
0.999... im Metamath Proof Explorer (englisch)
A Friendly Chat About Whether 0.999… = 1 bei BetterExplained (englisch)
Vihart: 9.999... reasons that .999... auf YouTube, 25. März 2012, abgerufen am 10. März 2021 (englisch).

Einzelnachweise

William Byers argumentiert, wer aufgrund solcher Beweise 0,999… = 1 akzeptiere, aber die Mehrdeutigkeit nicht aufgelöst habe, habe die Gleichung nicht wirklich verstanden (Byers S. 39–41).
Im Artikel Stellenwertsystem#Lexikographische Ordnung wird gezeigt, dass der Ordnungshomomorphismus, der den Zeichenketten bspw. über einem Alphabet {0, 1, …, 9} eine reelle Zahl zuordnet und der die Zeichenketten lexikographisch und die reellen Zahlen wie üblich anordnet, niemals ein Ordnungsisomorphismus sein kann.
Rudin S. 61, Theorem 3.26; J. Stewart S. 706.
Euler S. 170.
Grattan-Guinness S. 69; Bonnycastle S. 177.
Der Grenzwert folgt zum Beispiel aus Rudin S. 57, Theorem 3.20e.
Davies S. 175; Smith und Harrington S. 115.
Griffiths und Hilton S. xiv sowie Pugh S. 10 ziehen Dedekindsche Schnitte den Axiomen vor. Für die Nutzung der Schnitte in Lehrbüchern, siehe Pugh S. 17 oder Rudin S. 17. Für Standpunkte in Bezug auf Logik, siehe Pugh S. 10, Rudin S. ix oder Munkres S. 30.
Enderton S. 113 verwendet eine ähnliche Definition, die dem entspricht, was hier als linke Menge bezeichnet wird.
Rudin S. 17–20, Richman S. 399 und Enderton S. 119 nennen diesen Schnitt 1*, 1⁻ und 1_R und identifizieren ihn mit der traditionellen reellen Zahl 1. Was Rudin und Enderton einen Dedekindschen Schnitt nennen, nennt Richman nonprincipal Dedekind cut.
J. J. O’Connor, E. F. Robertson: History topic: The real numbers: Stevin to Hilbert. (Nicht mehr online verfügbar.) Archiviert vom Original am 29. September 2007; abgerufen am 23. Januar 2014.
Komornik und Loreti S. 636.
Kempner S. 611; Petkovšek S. 409.
Pugh S. 97; Alligood, Sauer und Yorke S. 150–152. Protter und Morrey S. 507 und Pedrick S. 29 weisen diese Beschreibung als Aufgabe an.
Preis für Rechen-As: Schülerin stellt klügste Mathefrage. In: Spiegel Online. 24. April 2008, abgerufen am 17. Januar 2015.
Lightstone S. 245–247.
Katz und Katz 2010.
Stewart 2009, S. 175; die vollständige Diskussion über 0,999… findet sich in 172–175.
Katz und Katz 2010b
R. Ely 2010.
Richman S. 397–399.
Richman S. 398–400. Rudin S. 23 verordnet diese alternative Konstruktion (allerdings über die rationalen Zahlen) als letzte Aufgabe von Kapitel 1.
Fjelstad S. 11.
Dass es bei diesen tatsächlich eine passende Betragsfunktion gibt, wird im Artikel Proendliche Zahl#10-adische Zahlen gezeigt.
DeSua S. 901–903.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] William Byers argumentiert, wer aufgrund solcher Beweise 0,999… = 1 akzeptiere, aber die Mehrdeutigkeit nicht aufgelöst habe, habe die Gleichung nicht wirklich verstanden (Byers S. 39–41).

[2] Im Artikel Stellenwertsystem#Lexikographische Ordnung wird gezeigt, dass der Ordnungshomomorphismus, der den Zeichenketten bspw. über einem Alphabet {0, 1, …, 9} eine reelle Zahl zuordnet und der die Zeichenketten lexikographisch und die reellen Zahlen wie üblich anordnet, niemals ein Ordnungsisomorphismus sein kann.

[3] Rudin S. 61, Theorem 3.26; J. Stewart S. 706.

[4] Euler S. 170.

[5] Grattan-Guinness S. 69; Bonnycastle S. 177.

[6] Der Grenzwert folgt zum Beispiel aus Rudin S. 57, Theorem 3.20e.

[7] Davies S. 175; Smith und Harrington S. 115.

[8] Griffiths und Hilton S. xiv sowie Pugh S. 10 ziehen Dedekindsche Schnitte den Axiomen vor. Für die Nutzung der Schnitte in Lehrbüchern, siehe Pugh S. 17 oder Rudin S. 17. Für Standpunkte in Bezug auf Logik, siehe Pugh S. 10, Rudin S. ix oder Munkres S. 30.

[9] Enderton S. 113 verwendet eine ähnliche Definition, die dem entspricht, was hier als linke Menge bezeichnet wird.

[10] Rudin S. 17–20, Richman S. 399 und Enderton S. 119 nennen diesen Schnitt 1*, 1⁻ und 1_R und identifizieren ihn mit der traditionellen reellen Zahl 1. Was Rudin und Enderton einen Dedekindschen Schnitt nennen, nennt Richman nonprincipal Dedekind cut.

[MacTutor-11] J. J. O’Connor, E. F. Robertson: History topic: The real numbers: Stevin to Hilbert. (Nicht mehr online verfügbar.) Archiviert vom Original am 29. September 2007; abgerufen am 23. Januar 2014.

[12] Komornik und Loreti S. 636.

[13] Kempner S. 611; Petkovšek S. 409.

[14] Pugh S. 97; Alligood, Sauer und Yorke S. 150–152. Protter und Morrey S. 507 und Pedrick S. 29 weisen diese Beschreibung als Aufgabe an.

[SPON-549422-15] Preis für Rechen-As: Schülerin stellt klügste Mathefrage. In: Spiegel Online. 24. April 2008, abgerufen am 17. Januar 2015.

[16] Lightstone S. 245–247.

[17] Katz und Katz 2010.

[18] Stewart 2009, S. 175; die vollständige Diskussion über 0,999… findet sich in 172–175.

[19] Katz und Katz 2010b

[20] R. Ely 2010.

[21] Richman S. 397–399.

[22] Richman S. 398–400. Rudin S. 23 verordnet diese alternative Konstruktion (allerdings über die rationalen Zahlen) als letzte Aufgabe von Kapitel 1.

[Fjelstad-23] Fjelstad S. 11.

[24] Dass es bei diesen tatsächlich eine passende Betragsfunktion gibt, wird im Artikel Proendliche Zahl#10-adische Zahlen gezeigt.

[25] DeSua S. 901–903.