Feynman-Punkt
Der Feynman-Punkt ist eine Folge von sechsmal der Ziffer 9 ab der 762. Nachkommastelle der Dezimaldarstellung von Pi.[1]
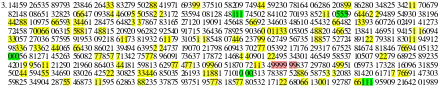
Geschichte
Sie ist nach dem Physiker Richard Feynman benannt, der angeblich einst in einer Vorlesung sagte, dass er die Stellen von Pi bis zu diesem Punkt auswendig lernen wolle, damit er beim anschließenden Rezitieren scherzhaft „neun neun neun neun neun neun und so weiter“ sagen könne, was implizieren würde, dass Pi eine rationale Zahl wäre.[2] Es ist allerdings unklar, ob diese Idee wirklich von Feynman stammt: Sie kommt in keinem seiner Bücher und in keiner seiner Biographien vor, und Feynmans Biographen James Gleick ist die Geschichte unbekannt.[3] Die früheste bekannte Erwähnung der Idee, Pi bis zu den sechs Neunen aufzusagen, findet sich in Douglas Hofstadters Buch Metamagicum (1985),[4] in dem Hofstadter schreibt:
„Als irrer Schüler habe ich einmal 380 Ziffern von π auswendig gelernt. In meinem unbefriedigten Ehrgeiz wollte ich jenen Punkt erreichen – in der Dezimalausbreitung die 762. Stelle – wo es mit 999999 weitergeht, so daß ich die π-Konstante laut hätte aufsagen können, bis ich zu diesen sechs Neunern gekommen wäre, um dann mit einem verschmitzten ‚und so weiter‘ aufhören zu können.“
Weitere Statistiken
Es wurde die (bisher unbewiesene) Vermutung aufgestellt, dass Pi eine normale Zahl sei. Die Wahrscheinlichkeit, dass für eine gegebene zufällig gewählte normale Zahl eine bestimmte sechsstellige Zahlenfolge bereits so früh in der Dezimaldarstellung auftritt, ist normalerweise nur 0,08 %[2] (oder, noch genauer, 0,0762 %). Wenn die Folge sich allerdings überschneiden darf (wie beispielsweise bei 123123 oder 999999), ist die Wahrscheinlichkeit geringer. Die Wahrscheinlichkeit von sechs aufeinanderfolgenden Neunen zu diesem frühen Zeitpunkt ist etwa 10 % weniger, oder 0,0686 %. Die Wahrscheinlichkeit, dass sich eine beliebige Zahl sechsmal in den ersten 762 Ziffern wiederholt, ist allerdings zehnmal so groß, also 0,686 %.
Man könnte allerdings die Frage stellen, warum man über eine Wiederholung von sechs Ziffern spricht. Man hätte ebenso über die Wahrscheinlichkeit in den ersten drei Ziffern dreimal die gleiche Zahl zu finden, oder ebenso in den ersten zehn Ziffern viermal die gleiche, in den ersten 100 Ziffern fünfmal die gleiche und so weiter. Jede dieser Möglichkeiten hat etwa eine Wahrscheinlichkeit von 1 %. Wenn man demnach die Wiederholungen bis zur Länge 12 betrachtet, besteht ungefähr eine 10-prozentige Wahrscheinlichkeit, etwas so außergewöhnliches wie den Feynman-Punkt zu finden. Aus diesem Blickwinkel betrachtet ist die Tatsache, dass wir tatsächlich eine Wiederholung von einigen Ziffern an dieser Stelle finden, nicht überraschend.
Die nächste Folge von sechs identischen aufeinanderfolgenden Ziffern besteht wieder aus Neunen und beginnt ab der Position 193.034.[2] Die danach nächste Sequenz von sechs nachfolgenden identischen Ziffern fängt mit der Zahl 8 an Stelle 222.299 an und die Ziffer 0 wiederholt sich ab Position 1.699.927 sechsmal. Eine Folge von neun Sechsen (666666666) taucht an der Position 45.681.781 auf.[6] und eine Folge von 9 Neunen ist an Position 590.331.982, die nächste bei 640.787.382 zu finden.[7]
Der Feynman-Punkt ist gleichzeitig das erste Vorkommen von vier oder fünf aufeinanderfolgenden gleichen Ziffern in Pi. Die nächste Stelle, an der vier gleiche Ziffern aufeinanderfolgen, ist die Ziffer 7 bei Position 1.589.[6]
Die Positionen in Pi, an denen die Ziffer 9 jeweils zum ersten Mal 1- bis 9-mal hintereinander vorkommt, sind 5, 44, 762, 762, 762, 762, 1.722.776, 36.356.642 und 564.665.206; Folge A048940 in OEIS.[1]
Siehe auch
Weblinks
- Eric W. Weisstein: Feynman Point. In: MathWorld (englisch).
Einzelnachweise
- D. Wells: The Penguin Dictionary of Curious and Interesting Numbers. Penguin Books, Middlesex, England 1986, ISBN 0-14-026149-4, S. 51.
- J. Arndt, C. Haenel: Pi – Unleashed. Springer, Berlin 2001, ISBN 3-540-66572-2, S. 3.
- David Brooks: Wikipedia turns 15 on Friday (citation needed). In: Concord Monitor, 12. Januar 2016. Abgerufen am 10. Februar 2016.
- Rudy Rucker: Douglass Hofstadter’s Pi in the Sky. In: The Washington Post, 5. Mai 1985. Abgerufen am 4. Januar 2016.
- Douglas Hofstadter: Metamagicum. Deutscher Taschenbuch Verlag, München 1994, ISBN 3-608-93089-2, S. 133.
- Pi Search.
- One billion digits of pi. Berechnet mit editpad lite 7. Auf: stuff.mit.edu.