Émile Lemoine
Émile Michel Hyacinthe Lemoine [emil ləmwan] (* 22. November 1840 in Quimper, Frankreich; † 21. Februar 1912 in Paris) war ein französischer Mathematiker und Ingenieur. Er wurde vor allem für seinen Beweis des Zusammentreffens der Symmedianen in einem Punkt, dem Lemoinepunkt, berühmt.

Leben
Lemoine wurde am 22. November 1840 in Quimper in der Bretagne geboren. Sein Vater, ein Hauptmann der französischen Armee, war 1808 an der Gründung der Prytanée national militaire in La Flèche beteiligt. Deswegen erhielt Lemoine ein Stipendium für den Besuch dieser Schule. Bereits in seiner Schulzeit veröffentlichte er im Magazin Nouvelles annales de mathématiques einen Artikel über geometrische Relationen im Dreieck. Als er zwanzig war, im selben Jahr, als sein Vater starb, wurde Lemoine in die École polytechnique aufgenommen. Während er dort studierte, wirkte er bei der Gründung eines Kammerensembles namens La Trompette mit, in dem er wahrscheinlich Trompete spielte. Camille Saint-Saëns komponierte mehrere Stücke für das Ensemble.[1]
Nach seiner Graduation im Jahr 1866 wollte Lemoine zunächst Rechtswissenschaftler werden. Er ließ aber von diesem Vorhaben ab, da seine politischen und religiösen Einstellungen im Widerspruch mit den Idealen der damaligen Regierung standen. Deshalb studierte und lehrte er in der nächsten Zeit an verschiedenen Institutionen, wie der École d’Architecture, École des Mines, École des Beaux-Arts und der École de Médecine. Des Weiteren arbeitete er als Privatlehrer, bevor er die Ernennung zum Professor an der École Polytechnique annahm.
Als Lemoine im Jahr 1870 am Kehlkopf erkrankte, beendete er seine Lehrtätigkeit und ging für kurze Zeit nach Grenoble. Nach seiner Rückkehr nach Paris, veröffentlichte er einige Ergebnisse seiner mathematischen Forschungen. Am Handelsgerichtshof in Paris wurde er in diesem Jahr Ingenieurconsulent. In der folgenden Zeit gründete er einige wissenschaftliche Vereinigungen und Journale, unter anderem die Société Mathématique de France, die Société de Physique und das Journal de Physique.
Beim Treffen der Association Française pour l’Avancement des Sciences im Jahr 1874, von der er ebenfalls ein Gründungsmitglied war, präsentierte Lemoine sein Werk Note sur les propriétés du centre des médianes antiparallèles dans un triangle, das später zu seinen berühmtesten Werken zählen sollte. In dieser Schrift bewies er, dass die Symmendianen sich in einem Punkt schneiden, der später ihm zu Ehren Lemoinepunkt genannt wurde.
Nach einigen Jahren beim französischen Militär war er als Ingenieur bis 1896 für die Gasversorgung von Paris zuständig. In diesen und den folgenden Jahren verfasste Lemoine den Großteil seiner Werke, wie La Géométrographie ou l’art des constructions géométriques, das er 1888 auf dem Treffen der Association Française in Oran, Algerien vorstellte. In dem Werk beschreibt Lemoine ein System, mit dem die Komplexität von Konstruktionen angegeben werden kann.
Weitere Werke aus dieser Zeit waren eine Reihe von Schriften über die Beziehung von Gleichungen und geometrischen Objekten, die er transformation continue (kontinuierliche Transformation) nannte. Das Thema der Werke, hat nichts mit dem Transformationsbegriff der heutigen Zeit zu tun.
1894 verwirklichte Lemoine ein länger geplantes Vorhaben und gründete zusammen mit Charles-Ange Laisant, einem Freund von der École polytechnique, ein weiteres mathematisches Journal mit dem Namen L'intermédiaire des mathématiciens. Lemoine war mehrere Jahre der Chefredakteur des Journals und unterstützte so die Mathematik weiter, obwohl er seit 1895 nicht mehr forschte.
Émile Lemoine starb am 21. Februar 1912 in seiner Heimatstadt Paris.
Leistungen
Nathan Altshiller-Court sagt über Lemoine, dass er, neben Henri Brocard und Joseph Neuberg, einer der Begründer der modernen Dreiecksgeometrie (18. Jahrhundert oder später) sei.[2]
Zu dieser Zeit beschäftigte sich die Dreiecksgeometrie vor allem mit Untersuchungen, ob bestimmte Punkte auf einem Kreis oder einer Linie liegen oder ob sich drei Linien in einem Punkt schneiden. Lemoine fügte sich mit seinen Werken zur Dreiecksgeometrie perfekt in den damaligen Zeitgeist ein, da auch er in seinen Werken die Schnittpunkte von Linien und Kreisen untersuchte.
Auf dem Treffen der Académie des sciences im Jahr 1902, bekam Lemoine den mit 1000-Franc dotierten Francœur Preis,[3] den er mehrere Jahre lang erhielt.[4]
Lemoinepunkt
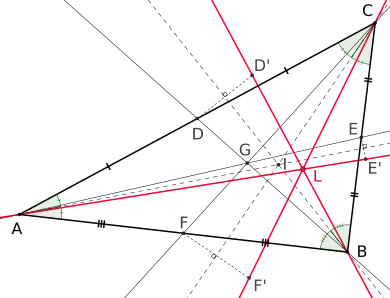
Winkelhalbierende (grün), Seitenhalbierende (blau),
Symmedianen (rot)
In seinem Werk Note sur les propriétés du centre des médianes antiparallèles dans un triangle (1874) bewies Lemoine, dass sich die Symmedianen eines Dreiecks in einem Punkt schneiden. Lemoine nannte den Punkt centre des médianes antiparallèles. Des Weiteren führte er in dem Werk Eigenschaften des Punkts an. Da sich vor Lemoine schon einige Mathematiker wie Grebe oder P. Hossard mit dem Punkt beschäftigt hatten, bestand Lemoines Leistung nur in der wissenschaftlichen Zusammenfassung der Ergebnisse. Diese organisatorischen Verdienste haben dazu geführt, dass der Punkt ab 1876 meist Lemoinepunkt oder lemoinescher Punkt genannt wurde.[5] Anderen Quellen zufolge schlug Joseph Jean Baptiste Neuberg (1840–1926) im Jahr 1884 vor, den Punkt zu Ehren Lemoines Lemoinepunkt zunennen.[6]
E. Hain nannte den Punkt 1876 den Punkt Grebeschen Punkt, da er fälschlicherweise dachte, dass Ernst Wilhelm Grebe (1804–1874) den Punkt 1847 als erster behandelt hatte. Daraufhin wurde der Punkt eine Zeit lang in Deutschland Grebe-Punkt (bzw. Grebescher Punkt) genannt, in Frankreich allerdings Lemoinepunkt. Robert Tucker (1832–1905) schlug aus Gründen der Einheitlichkeit vor, den Punkt Symmedianenpunkt zu nennen.
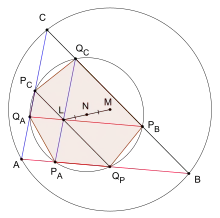
Zieht man durch den Lemoinepunkt Parallelen zu den drei Dreiecksseiten und verbindet man die Schnittpunkte der Parallelen mit den Dreiecksseiten miteinander, so entsteht ein Sechseck, das sogenannte lemoinesche Sechseck.[7] Die Parallelen werden oft Lemoine-Parallelen genannt. Der Umkreis des Sechsecks wird erster lemoinescher Kreis genannt. Der Mittelpunkt dieses Kreises liegt in der Mitte zwischen dem Lemoinepunkt und dem Schnittpunkt der Mittelsenkrechten (also dem Umkreismittelpunkt) des Dreiecks.[8] Zieht man die Antiparallelen (auch Lemoine-Antiparallelen genannt) durch den Lemoinepunkt eines Dreiecks, so schneiden sie sich mit den Seiten des Dreiecks in sechs Punkten. Verbindet man diese, erhält man das Cosinus-Sechseck.[9] Der Umkreis dieses Sechsecks heißt Cosinus-Kreis oder zweiter lemoinescher Kreis.[10]
Konstruktionssystem
Lemoine entwickelte ein System, von ihm Géométrographie genannt, mit dem die „Einfachheit“ geometrischer Konstruktionen bewertet werden konnte. Er erkannte auch, dass diese Bezeichnung eigentlich falsch ist und besser „Maß der Kompliziertheit“ heißen sollte. Die Einfachheit einer Konstruktion kann durch die Anzahl der benötigen Grundoperationen bestimmt werden. Die Anzahl der Ausführungen der Operationen 1, 2 und 4 nennt Lemoine die Genauigkeit der Konstruktion. Die von Lemoine genannten Grundoperationen sind:
- Platzieren eines Zirkels auf einem gegebenen Punkt,
- Platzieren eines Zirkels auf einer gegebenen Linie,
- Zeichnen eines Kreises mit dem Zirkel auf dem Punkt oder der Linie,
- Anlegen eines Lineal an eine Linie und
- Erweitern der Linie mit dem Lineal.[11]

Dieses System ermöglichte auch existierende Konstruktionen leichter zu vereinfachen. Allerdings besaß Lemoine keinen hinreichend allgemeinen Algorithmus, mit dem er beweisen konnte, ob eine Lösung optimal ist oder ob es eine bessere gibt. Lemoine behandelte das System in dem Werk La Géométrographie ou l'art des constructions géométriques, das er beim Treffen der Association Française in Pau (1892), in Besançon (1893) und Caen (1894) präsentierte. Er veröffentlichte weitere Schriften zu diesem Thema in Mathesis (1888), Journal des mathématiques élémentaires (1889) und Nouvelles annales de mathématiques (1892). Infolge der Präsentationen und der Vorstellung in einigen Journalen fand das Konstruktionssystem in Deutschland und Frankreich gewisse Aufmerksamkeit, wurde aber schließlich vergessen, da die Mathematiker der damaligen Zeit längere aber einfachere Lösungen kürzeren und komplizierten vorzogen. Aus heutiger Sicht lässt sich sagen, dass Lemoine seiner Zeit voraus war, und seine Géométrographie einen beachtlichen Ansatz in der Messung der Kompliziertheit und Optimierung von Algorithmen darstellt.[12]
In seinem Werk La Géométrographie ou l'art des constructions géométriques behandelte Lemoine das Apollonische Problem, das von Apollonios von Perge aufgestellt worden war: Zu drei gegebenen Kreisen soll ein vierter Kreis so konstruiert werden, der die anderen Kreise tangiert. Das Problem war 1816 schon von Joseph Gergonne mit einer Einfachheit von 400 (479 laut Coolidge: A history of Geometrical Methods) gelöst worden, Lemoine aber präsentierte eine Lösung der Einfachheit 199. Heute sind noch einfachere Lösungen bekannt, wie die von Frederick Soddy aus dem Jahr 1936 und die von David Eppstein aus dem Jahr 2001.[13]
Schriften
- Sur quelques propriétés d'un point remarquable du triangle (1873)
- Note sur les propriétés du centre des médianes antiparallèles dans un triangle (1874)
- Sur la mesure de la simplicité dans les tracés géométriques (1889)
- Sur les transformations systématiques des formules relatives au triangle (1891)
- Étude sur une nouvelle transformation continue (1891)
- La Géométrographie ou l'art des constructions géométriques (1892)
- Une règle d'analogies dans le triangle et la spécification de certaines analogies à une transformation dite transformation continue (1893)
- Applications au tétraèdre de la transformation continue (1894)
Literatur
- Nathan Altshiller-Court: College geometry. Barnes & Noble, inc., New York 1952
- Siegfried Gottwald (Hrsg.): Lexikon bedeutender Mathematiker. Harri Deutsch, Thun 1990, ISBN 3-8171-1164-9.
- Katrin Weiße, Peter Schreiber: Zur Geschichte des Lemoineschen Punktes. In: Peter Richter (Hrsg.): Beiträge zur Geschichte, Philosophie und Methodologie der Mathematik. Ernst-Moritz-Arndt-Universität Greifswald, Neubrandenburg 1988, ISSN 0138-2853, S. 73–74.
Weblinks
- John J. O’Connor, Edmund F. Robertson: Émile Lemoine. In: MacTutor History of Mathematics archive.
- Biographie Lemoines auf der Seite der University of Evansville (englisch)
- Digitalisierte Werke Lemoines auf Numdam.org (englisch)
Einzelnachweise
- http://www.morrisonfoundation.org/charles lenepveu.htm (Link nicht abrufbar)
- Clark Kimberling: Triangle Geometers. University of Evansville. Abgerufen am 20. November 2008.
- Disseminate (englisch, PDF) In: Bulletin of the American Mathematical Society. American Mathematical Society. S. 273. 1903. Abgerufen am 21. November 2008.
- Notes (englisch, PDF; 554 kB) In: Bulletin of the American Mathematical Society. American Mathematical Society. S. 424. 1912. Abgerufen am 21. November 2008.
- Katrin Weiße, Peter Schreiber: Zur Geschichte des Lemoineschen Punktes. In: Peter Richter (Hrsg.): Beiträge zur Geschichte, Philosophie und Methodologie der Mathematik (II). ISSN 0138-2853, S. 73–74.
- Carl D. Meyer: Earliest Known Uses of the Words of Mathematics (englisch, PDF) S. 199. 2000. Abgerufen am 20. November 2008.
- Eric W. Weisstein: Lemoine Hexagon (englisch) Abgerufen am 23. Oktober 2008.
- Eric W. Weisstein: First Lemoine Circle (englisch) Abgerufen am 23. Oktober 2008.
- Eric W. Weisstein: Cosine Hexagon (englisch) Abgerufen am 20. November 2008.
- Eric W. Weisstein: Cosine Circle (englisch) Abgerufen am 20. November 2008.
- Lemoine, Émile. La Géométrographie ou l'art des constructions géométriques. (1903), Scientia, Paris (französisch)
- Julian Lowell Coolidge: A history of geometrical methods. Dover Publications, inc., New York 1963
- David Gisch, Jason M. Ribando: Apollonius’ Problem: A Study of Solutions and Their Connections (englisch, PDF; 891 kB) In: American Journal of Undergraduate Research. University of Northern Iowa. 29. Februar 2004. Abgerufen am 21. November 2008.