Lemoinepunkt

Der Lemoinepunkt eines Dreiecks, auch Lemoinescher Punkt, Grebepunkt oder Symmedianenpunkt genannt, ist ein ausgezeichneter Punkt im Dreieck. Er ist der Schnittpunkt der an den Winkelhalbierenden gespiegelten Seitenhalbierenden, der Symmediane.

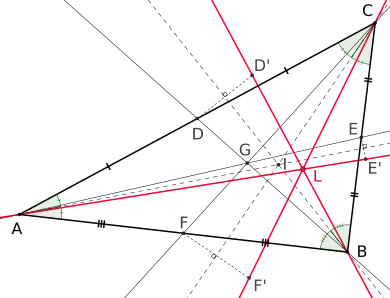
Lemoine-Punkt L als Schnittpunkt der Symmediane (rot)

Eigenschaften

Der Lemoinepunkt ist definitionsgemäß isogonal konjugiert zum Schwerpunkt.
Wenn wir das Dreieck mit ABC bezeichnen und den Lemoinepunkt mit L, dann sind die Abstände des Punktes L zu den Geraden BC, CA und AB proportional zu den Längen der Seiten BC, CA und AB des Dreiecks ABC.
Der Lemoinepunkt ist Lösung eines gelegentlich wichtigen Optimierungsproblems: Wenn wir einen Punkt P in der Ebene des Dreiecks ABC betrachten, dann ist die Summe der Quadrate der Abstände von dem Punkt P zu den Seiten BC, CA und AB genau dann minimal, wenn P mit dem Lemoinepunkt L des Dreiecks ABC übereinstimmt.
Dieses Optimierungsproblem wird ebenfalls gelöst bzw. der Lemoinepunkt gefunden, wenn die drei Seiten des Dreiecks durch drei lineare Gleichungen der entsprechenden Geraden in Hesse-Normalform in zwei Variablen ausgedrückt werden und eine ausgleichende Lösung des überbestimmten linearen Gleichungssystems mit Hilfe der Methode der kleinsten Quadrate bestimmt wird.
Der Lemoinepunkt des größeren Dreiecks, das durch die drei Ankreismittelpunkte bestimmt wird, ist der sogenannte Mittenpunkt des Dreiecks.

Koordinaten

Lemoine-Punkt (Symmedianenpunkt, Grebe-Punkt, $X_{6}$ )
Trilineare Koordinaten	$a\,:\,b\,:\,c=\,\sin \alpha \,:\,\sin \beta \,:\,\sin \gamma$
Baryzentrische Koordinaten	$a^{2}\,:\,b^{2}\,:\,c^{2}$

Geschichte

Der Punkt ist in England und Frankreich nach dem französischen Mathematiker Émile Lemoine und in Deutschland auch nach dem deutschen Mathematiker Ernst Wilhelm Grebe benannt, die beide zu ihm publizierten. Allerdings war der Punkt bereits vor ihren Publikationen bekannt.

Literatur

Roger A. Johnson: Advanced Euclidean Geometry. Dover 2007, ISBN 978-0-486-46237-0, S. 213, 268, 271, 303 (Erstveröffentlichung 1929 bei der Houghton Mifflin Company (Boston) unter dem Titel Modern Geometry).

Weblinks

Eric W. Weisstein: Symmedian Point. In: MathWorld (englisch).
X6 Der Symmedian Point. Eine umfangreiche Darstellung mit diversen weiterführenden Aussagen

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.