Symmediane
So wie man eine Seitenhalbierende eines Dreiecks auch als Median bezeichnet, nennt man das Spiegelbild einer Seitenhalbierenden an der entsprechenden Winkelhalbierenden (also an der Winkelhalbierenden, die von derselben Ecke ausgeht wie die Seitenhalbierende) Symmedian. Der Begriff ist eine Abkürzung für "symmetrischer Median", kommt aus dem Griechischen und bedeutet "Spiegelung an der Mittellinie".
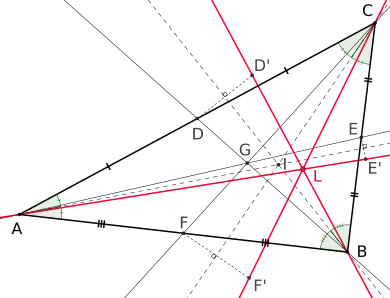
Dreieck mit Seitenhalbierenden (schwarz), Winkelhalbierenden (gestrichelt) und Symmedianen (rot). L = Symmedianenpunkt
Die drei Symmediane eines Dreiecks schneiden einander in einem Punkt, dem so genannten lemoineschen Punkt (Lemoinepunkt), der auch Grebepunkt oder Symmedianenpunkt genannt wird. Dies lässt sich mit Hilfe des Satzes von Ceva beweisen.
Der Schnittpunkt der Symmediane ist ein nicht-kanonischer ausgezeichneter Punkt des Dreiecks.
Literatur
- Roger A. Johnson: Advanced Euclidean Geometry. Dover 2007, ISBN 978-0-486-46237-0, S. 213, 268, 271, 303 (Erstveröffentlichung 1929 bei der Houghton Mifflin Company (Boston) unter dem Titel Modern Geometry).
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.