Zauberwürfel

Der Zauberwürfel (manchmal auch wie im englischsprachigen Raum Rubik’s Cube, Rubiks Würfel, genannt) ist ein Drehpuzzle, das 1974[1][2] von dem ungarischen Bauingenieur und Architekten Ernő Rubik erfunden wurde. 1980 wurde es mit dem Sonderpreis Bestes Solitärspiel des Kritikerpreises Spiel des Jahres ausgezeichnet. Er erfreute sich insbesondere Anfang der 1980er Jahre großer Beliebtheit, die Speedcubing-Community wächst seit den 2000er Jahren stetig.

Zauberwürfel in Grundstellung

Zauberwürfel mit teilweise gedrehter Seite

Bewegung des Zauberwürfels

Beschreibung

Bei einem Zauberwürfel in Standardgröße handelt es sich um einen Würfel mit einer Kantenlänge von 57 mm, gemessen an den Mittelachsen. Es gibt allerdings auch größere oder kleinere Varianten wie mit einer Kantenlänge von 54,4 mm. Der Würfel ist in der Höhe, Breite und Tiefe in jeweils drei Lagen unterteilt, die sich durch 90-Grad-Drehungen um ihre jeweilige Raumachse drehen lassen. Dadurch können Position und Lage von 20 der insgesamt 26 Steine (die Mittelsteine sind fest verbaut) fast beliebig verändert werden. Auf die nach außen sichtbaren Flächen der Steine sind kleine Farbflächen geklebt oder die Steine selbst sind gefärbt. In der Grundstellung sind die Steine so geordnet, dass jede Seite des Würfels eine einheitliche, aber von Seite zu Seite andere Farbe hat. Der Standardwürfel ist in der Grundfarbe schwarz und die Farbgebung der Flächen entspricht Weiß gegenüber von Gelb, Blau gegenüber von Grün und Rot gegenüber von Orange. Die Orientierung der Farben beim Betrachten des weiß-blau-roten Ecksteins entspricht Weiß oben, Blau rechts und Rot links. Bei einem Würfel in der Grundfarbe Weiß wird die weiße Fläche oftmals durch eine schwarze getauscht.

Ziel ist es für gewöhnlich, den Würfel wieder in seine Grundstellung zu bewegen, nachdem die Seiten in eine zufällige Stellung gedreht wurden. Auf den ersten Blick erscheint diese Aufgabe außerordentlich schwierig, jedoch wurden schon frühzeitig Strategien entwickelt, deren Kenntnis ein relativ leichtes Lösen gestattet.

Aufbau und Komponenten

Der Zauberwürfel hat insgesamt 26 einzelne Steine:

Mittelstein: Die sechs Steine in der Mitte der Würfelflächen sitzen auf dem Achsenkreuz im Inneren des Würfels und daher zueinander konstruktionsbedingt immer in derselben relativen Lage. Die Farbe des Mittelsteines bestimmt, welche anderen Steine auf diese Seite gehören und welche Orientierung sie haben müssen. Mittelsteine sind einfarbig.
Kantenstein: Die zwölf Kantensteine verbinden je zwei angrenzende Flächen und werden von den Mittelsteinen der beiden Flächen gehalten. Kantensteine haben zwei Farben.
Eckstein: Die acht Ecksteine verbinden je drei angrenzende Flächen in den Ecken. Sie werden von den drei benachbarten Kantensteinen in Position gehalten und haben jeweils drei Farben.

Geöffneter Zauberwürfel
Achsenkreuz mit sechs Mittelsteinen (einfarbig)
Zwölf Kantensteine (zweifarbig)
Acht Ecksteine (dreifarbig)

Geschichte

In der Sendung Der große Preis erklärte der Erfinder, er habe durch ein dreidimensionales Geduldsspiel seinen Studenten eine Möglichkeit geben wollen, ihr räumliches Denkvermögen zu trainieren, als ihm auffiel, dass sie schlechte Geometrie-Kenntnisse von der Schule mitbrachten. Schon früher brachte Rubik seine Interessen für Bildhauerei, Gestaltung und Geometrie in Einklang und bastelte phantasievolle, dreidimensionale Holzfiguren.

Innerhalb weniger Wochen im Jahre 1974[1][2] konstruierte Rubik den ersten Zauberwürfel, der aus 27 kleinen Holzblöcken bestand. Um die Bewegung der Steine zu ermöglichen, experimentierte er zunächst mit elastischen Bändern, die jedoch zu leicht rissen. Schließlich kam er auf die Idee, in den Prototyp ein Mittelstück, eine Art Stern aus drei sich kreuzenden Achsen zu integrieren. Die Kanten und Eckstücke ordnete er so an, dass sie um das Würfelzentrum verschoben werden konnten. Schließlich beklebte Rubik jede Seite der kleinen Würfel mit Papier in verschiedenen Farben und stellte so das Lehrmittel für seine Studenten fertig. Doch als er an dem Würfel zu drehen begann, bekam er plötzlich Probleme, den ursprünglichen Zustand wiederherzustellen. Rubik sagte später: „Es war wie ein Geheimcode, den ich selbst erfunden hatte, aber nicht mehr entschlüsseln konnte!“ Als er seinen Würfel wieder geordnet hatte, empfand er ein Gefühl der Freiheit. Da begriff Rubik, dass in seiner Erfindung viel mehr steckte als nur ein Lehrmittel. Recherchen ergaben, dass es noch kein ähnliches Spielzeug auf der Welt gab.[3] Nachdem Rubik für den Würfel am 28. Oktober 1976 das ungarische Patent Nr. 170062 erteilt worden war,[4] hielt der Würfel im Dezember 1977 Einzug in die „kapitalistische Welt“, als ein Exemplar des Würfels der in Großbritannien ansässigen Firma Pentangle zugesandt wurde. Dieses Unternehmen erwarb daraufhin die Lizenz zum Vertrieb des Würfels in Großbritannien. Die Regierung in Ungarn vergab allerdings 1979 die weltweiten Verkaufsrechte für den Würfel an den US-amerikanischen Hersteller Ideal Toy Corporation (in Europa auch unter Arxon bekannt). Darin waren vertragswidrig auch die Rechte für das Vereinigte Königreich enthalten. Ideal Toy Corporation erlaubte Pentangle den Verkauf des Würfels an Geschenk-, aber nicht an Spielzeuggeschäfte. Anfangs machte Rubiks Idee unter Wissenschaftlern die Runde. Auf einem internationalen Mathematik-Kongress in Helsinki drehten Professoren stundenlang an ihrem Spielzeug herum. 1979 wurde der „Rubik’s Cube“ auf der Spielwarenmesse in Nürnberg vorgestellt. Ab dem 2. Juni 1980 war er in der Bundesrepublik im Verkauf erhältlich.

1981 hatte die Nachfrage nach dem mechanischen Geduldsspiel ihren Höhepunkt. Ideal Toy Corporation konnte die Nachfrage nicht befriedigen, was es fernöstlichen Billigprodukten ermöglichte, den Markt zu überschwemmen. Insgesamt wurden wohl etwa 160 Millionen Würfel allein bis zum Höhepunkt des Booms verkauft. Anfang 1982 brach die Nachfrage für den Würfel ein und mit ihr auch die Nachfrage nach vielen anderen Geduldsspielen.

Ernő Rubik war nicht der Erste, der sich mit dem Thema eines Spiels dieser Art beschäftigte. Schon 1957 entwickelte der Chemiker Larry D. Nichols einen ähnlichen Würfel, der allerdings nur aus 2 × 2 × 2 Teilen bestand und durch Magnete zusammengehalten wurde. Er ließ seinen Entwurf 1972 patentieren. 1984 gewann Nichols eine Patentklage gegen das Unternehmen, das den Rubik’s Cube in den USA vertrieb. Allerdings wurde dieses Urteil 1986 teilweise aufgehoben, sodass es nur noch den 2 × 2 × 2 großen Pocket Cube, engl. ‚Taschenwürfel‘, betraf.[5]

Auf der CeBIT 2009 wurde auch eine digitale Version des Würfels vorgestellt, die mit Leuchtdioden und Touchfeldern ausgestattet war.

Der deutsche Spielzeughersteller Simba Toys hat im November 2006 die Markenlöschung für die diesbezügliche europäische 3D-Marke[6] beantragt. Nichtigkeitsabteilung und Beschwerdekammer des vormaligen HABM verwarfen den Antrag jeweils als eindeutig unbegründet, das erstinstanzliche Gericht der Europäischen Union (EuG) bestätigte diese Entscheidung 2014.[7] Mit Urteil vom 10. November 2016[8] hob der Europäische Gerichtshof (EuGH) die Entscheidungen der Beschwerdekammer und des EuG zur erneuten Entscheidung auf. Die Entscheidung des EuGH bescheinigt dabei dem Löschungsantrag, dass für ihn gute Gründe sprächen, die die Vorinstanzen nicht berücksichtigt haben; eine Löschung wurde erwartet.[9]

Am 24. Oktober 2019 hat das Gericht der Europäischen Union (EuG) erneut entschieden und die Unionsmarke „Rubik’s Cube“ für nichtig erklärt.[10] Das EuG stellte dabei fest, dass diese Form nie als Unionsmarke hätte eingetragen werden dürfen, da die wesentlichen Merkmale dieser Form zur Erreichung der technischen Wirkung erforderlich sind, die in der Drehbarkeit des Rubik’s Cube besteht.[11]

Lösungsstrategie für den Zauberwürfel

Strategien, die mit möglichst wenigen Bewegungen des Würfels auskommen, sind meist nur mithilfe eines Computers oder umfangreicher Stellungstabellen umzusetzen. Andere, leichter zu merkende Strategien kommen mit wenigen Basiszügen aus, erfordern aber im Allgemeinen eine höhere Zahl von Bewegungen.

Algorithmen zur Lösung des Würfels werden mittels verschiedener Notationen aufgeschrieben. Der geläufigste Lösungsweg, bei dem die drei Ebenen des Würfels nacheinander geordnet werden, wird als „Layer-by-Layer“-Methode bezeichnet. Sie ähneln der publizierten Lösung, die der Spiegel (Nr. 4/1981) veröffentlichte. Im Bereich Speedcubing, wo es besonders auf die Schnelligkeit ankommt, werden zur Lösung des Zauberwürfels andere Varianten angewendet, zu nennen sind Jessica-Fridrich-Methode oder die nach Lars Petrus.

Buchstabennotation

Um Zugkombinationen für den Würfel zu notieren, wird jeder Aktion ein Buchstabe zugeordnet.

Abkürzung		Seite
dt.	engl.
V	F(ront)	vorne
H	B(ack)	hinten
R	R(ight)	rechts
L	L(eft)	links
O	U(p)	oben
U	D(own)	unten
x		Drehung des ganzen Würfels beim Betrachten der rechten Seite
y		Drehung des ganzen Würfels beim Betrachten der oberen Seite
z		Drehung des ganzen Würfels beim Betrachten der vorderen Seite
M		Drehung der Ebene zwischen L und R. Richtung wie Left
S		Drehung der Ebene zwischen F und B. Richtung wie Front
E		Drehung der Ebene zwischen Up und Down. Richtung wie Down

Ein Buchstabe bedeutet dabei stets eine Drehung der Seite um 90° im Uhrzeigersinn, ein ′ oder ⁻¹ gegen den Uhrzeigersinn relativ zur gerade betrachteten Seite. So ist beispielsweise die Drehung der Unterseite um 90° im Uhrzeigersinn (D) genau entgegengesetzt zur Drehung der Oberseite um 90° im Uhrzeigersinn (U). Eine 2 steht für eine Drehung der Ebene um 180°. Klein geschriebene Buchstaben bzw. Buchstaben, an denen ein kleines „w“ angehängt ist, die sich auf Seiten beziehen, bedeuten die Drehung von zwei Ebenen von der entsprechenden Seite aus betrachtet; beispielsweise für r bzw. Rw die rechte und dazu parallele mittlere Ebene. Manchmal werden noch weitere Buchstaben für Mittelschichtzüge verwendet. Um Fingertechniken oder Solves zu beschreiben, wird manchmal auch 2′ verwendet, um eine Drehung der rechten Seite um 180° gegen den Uhrzeigersinn zu verdeutlichen. Um sich Zugfolgen besser merken zu können, werden manchmal auch mehrere Züge in Klammern gesetzt.

Beispiel: Die folgende Kombination kippt zwei Kantensteine und lässt alle übrigen unverändert:

K₁ = B′ R2 B2 R B′ R′ B′ R2 F D B D′ F′

Grafische Notation

Alternativ dazu verwenden manche Anleitungen auch grafische Notationsformen, z. B. als dreidimensionale Würfeldarstellungen oder als 3×3-Ansicht der Vorderseite mit Pfeilen, die die Drehung der Würfelflächen angeben. Letztere haben den Nachteil, dass Operationen der (von vorne gesehen) mittleren und hinteren Würfelebene nur schwer darstellbar sind, beispielsweise durch eine zusätzliche Abwicklung der Oberseite. Es ist auch möglich, auf die Darstellung eines Würfels zu verzichten und ausschließlich Pfeile zu verwenden.[12]

Optimale Lösungen

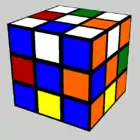
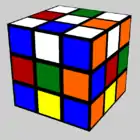
Der „Superflip“ ist die bekannteste Stellung, die nicht in weniger als 20 Zügen (Viertel- und halbe Drehungen) gelöst werden kann

Eine der drei bekannten Stellungen, die nicht in weniger als 26 Zügen (Vierteldrehungen) gelöst werden können

Um den Zauberwürfel aus einer gegebenen Stellung in die ursprüngliche Ausgangsstellung zu überführen, benötigt man eine bestimmte Mindestanzahl an Zügen. Ein Weg, der nur aus dieser Mindestanzahl an Schritten besteht, stellt somit eine optimale Lösung dar. (Zwischen den beiden Stellungen kann es mehrere verschiedene, aber gleich kurze Wege geben.)

Die Methode, von einer beliebigen Stellung aus einen solchen kürzesten Weg zu finden, wird als Gottes Algorithmus (engl. God’s Algorithm) bezeichnet. Diese Bezeichnung stammt von dem englischen Gruppentheoretiker John Conway oder einem seiner Kollegen in Cambridge.[13] In Anlehnung daran wird diejenige Anzahl Züge, die man mindestens zur Lösung des Zauberwürfels aus irgendeiner Stellung heraus benötigt – also die Länge der optimalen Wege für die „am weitesten“ von der Ausgangsstellung entfernten Stellungen –, Gottes Zahl genannt.

Es gibt zwei Möglichkeiten (Metriken), um die Würfelbewegungen (also die Schritte) zu zählen:

Vierteldrehungen (±90°) und Halbdrehungen (180°) von Seitenflächen werden als ein einzelner Zug betrachtet
Es werden die Vierteldrehungen einzeln gezählt.

Zählt man nur Vierteldrehungen, so kann man alleine durch Bewerten der Stellung des Würfels schon sagen, ob eine gerade oder ungerade Anzahl an Drehungen zum Lösen nötig ist.

Den ersten Algorithmus zum Finden einer optimalen Lösung formulierte Richard E. Korf, der 1997 zeigte, dass die durchschnittliche optimale Lösung 18 Züge (mit halben Drehungen) benötigt.[14] Er ging außerdem davon aus, dass nie mehr als 20 Züge erforderlich sind, jedoch konnte er das nicht beweisen. Bereits 1992 hatte Dik T. Winter eine Stellung (den sogenannten Superflip) gefunden, die 20 Züge benötigt. Den Beweis, dass diese Stellung tatsächlich nicht in weniger Zügen zu lösen ist, erbrachte Michael Reid im Jahr 1995.

Im März 2008 konnte der US-amerikanische Informatiker Tomas Rokicki mit gewaltigem Rechenaufwand zeigen, dass die Anzahl der Züge, die man bei richtiger Strategie maximal dazu benötigt, einen Rubik’s Cube aus jeder beliebigen Stellung in seine Ausgangslage zurückzudrehen, höchstens 25 sein kann,[15] was er im August durch verbesserte Computerunterstützung (durch den Software-Ingenieur John Welborn von Sony Pictures[16]) auf 22 reduzieren konnte.[17][18]

Im Juli 2010 bewies Tomas Rokicki zusammen mit Herbert Kociemba, Morley Davidson und John Dethridge die Vermutung, dass nie mehr als 20 Züge notwendig sind.[17][19] Es wurden 12.000.000 Stellungen gefunden, die nicht in weniger als 20 Zügen gelöst werden können. Vermutlich gibt es insgesamt 490.000.000 solche Stellungen.[17]

Im August 2014 erfolgte dann die Berechnung der Gottes Zahl bezüglich der Metrik, bei der (ausschließlich) Vierteldrehungen gezählt werden. Zur Lösung sind nie mehr als 26 Vierteldrehungen notwendig. Die Stellung, die in nicht weniger als 26 Zügen gelöst werden kann, wurde bereits 1998 gefunden. Bei einem Würfel, der in dieser Maximalstellung ist, sind alle Ecken richtig platziert, aber die Kanten gedreht. Außerdem sind zwei (der drei) Paare von gegenüberliegenden Mitten getauscht.[20] Damit sind drei mögliche Maximalstellungen bekannt, die sich aber mathematisch nicht unterscheiden. Der Beweis, dass dies die einzigen sind, steht noch aus.

Speedcubing

Speedcuber können mit 45 bis 60 Bewegungen einen beliebig verdrehten Rubik’s Cube lösen. Beim Speedcubing, also dem Lösen auf Zeit, kommt es auf das schnelle Erkennen von Stellungen, das Verinnerlichen einer hohen Anzahl von Algorithmen, das Vorausplanen und Fingerfertigkeit an.[21] Im Speedcubing werden Landes-, Kontinental- und Weltmeisterschaften von der World Cube Association (WCA) ausgetragen.[22]

Normales Lösen

Die erste Weltmeisterschaft, veranstaltet vom Guinness-Buch der Rekorde, fand am 13. März 1981 in München statt. Die Würfel waren 40-mal verdreht und mit Vaseline eingerieben. Gewinner der Meisterschaft war Jury Fröschl aus München mit einer Rekordzeit von 38 Sekunden.

Der aktuelle Weltrekord für einen 3×3×3-Würfel liegt bei 3,47 Sekunden und wurde von Yusheng Du bei Wuhu Open 2018 aufgestellt.

Einhändiges Lösen (One-handed)

Der Rubik’s Cube ist das einzige Drehpuzzle, für das Wettkämpfe im einhändigen Lösen von der WCA veranstaltet werden. Wenn im Löseprozess beide Hände den Cube berührt haben (das muss nicht gleichzeitig passieren), wird der Versuch als DNF (Did not finish) angesehen, d. h. nicht gewertet. In der Inspektionsphase dürfen allerdings beide Hände den Cube berühren.

Der aktuelle Weltrekord, aufgestellt bei Bay Area Speedcubin' 20 2019 von Max Park, liegt bei 6,82 Sekunden.[23]

Blindfold Cubing

Eine andere bekannte Disziplin ist das Blindfold Cubing. Dabei prägt man sich zunächst den verdrehten Zauberwürfel ein und löst ihn dann mit verbundenen Augen, ohne ihn ein weiteres Mal zu sehen. In die Zeit fließen Inspektionszeit und Lösezeit ein. Tatsächlich prägt man sich nicht den ganzen Würfel ein, sondern oft nur die Reihenfolge der Algorithmen. Zur Lösung werden von „Anfängern“ meist Methoden eingesetzt, die möglichst wenige andere Steine pro Algorithmus ändern.

Der aktuelle Weltrekord, aufgestellt bei Florida Fall 2021 von Tommy Cherry, liegt bei 14,67 Sekunden.[23]

Multiple Blindfold Cubing

Zudem gibt es auch das Multiple Blindfold Cubing, eine Steigerung des Blindfold Cubings. Dabei prägt man sich zuerst so viele Würfel wie möglich ein, um sie danach mit verbundenen Augen alle blind zu lösen. Punkte gibt es nicht für die Zeit, sondern für die Anzahl gelöster Würfel minus die Anzahl ungelöster Würfel, die nach einer Stunde übrigbleiben.

Der aktuelle Weltrekord, aufgestellt bei OSU Blind Weekend 2019 von Graham Siggins, liegt bei 59/60 in 59:46 Minuten.[23]

Lösen mit möglichst wenigen Zügen (Fewest Moves)

In dieser Disziplin versuchen die Teilnehmer den Würfel in möglichst wenig Zügen zu lösen. Dafür haben sie nach offiziellen WCA-Regeln 60 Minuten Zeit.[24] Danach müssen sie eine maximal 80 Züge umfassende Lösung erarbeitet haben, welche sie dem Judge zur Prüfung übergeben.

Der Weltrekord von 16 Zügen wurde bei FMC 2019 von Sebastiano Tronto aufgestellt.[23]

Wie oben dargestellt kann jeder Würfel in 20 oder weniger Zügen gelöst werden; die meisten Stellungen sogar in 18 Zügen.[25]

Maschinelle Lösung

Von Berufsfachschülern gebauter Roboter zur Lösung des Zauberwürfels

Es gibt eine Reihe von Maschinen, die den Würfel mittels Bilderkennung und automatisierter Mechanik lösen können. So wurde der offizielle menschliche Rekord im Jahr 2011 erstmals von einer Robotik unterboten: CubeStormer 2 löste den Würfel in 5,27 Sekunden – der von einem Menschen (Feliks Zemdegs) aufgestellte Rekord lag bei 5,66 Sekunden.[26][27][23] 2014 löste CubeStormer 3 mittels eines Galaxy S4 und acht Lego Mindstorms EV3 den Würfel in 3,25 Sekunden.[28]

Im Januar 2016 wurde ein Video veröffentlicht, in dem ein Roboter den Zauberwürfel in 1,047 Sekunden lösen konnte. Weitere Lösungsversuche blieben beständig unter 1,2 Sekunden. Der Roboter „Sub1“ analysiert den Würfel mit vier USB-Webcams, gedreht wird er mit Hilfe von Schrittmotoren.[29][30]

Im November 2016 hat der Roboter „Sub1 reloaded“ auf der Münchner Fachmesse Electronica einen Zauberwürfel in 0,637 Sekunden gelöst. Eingebaut war der für das autonome Fahren entwickelte Microcontroller Infineon Aurix.[31]

Im März 2018 stellten Ben Katz und Jared Di Carlo eine weitere Maschine vor, die den Würfel in einer Rekordzeit von 0,38 Sekunden löst.[32]

Muster erstellen

Neben dem üblichen Lösen des Zauberwürfels ist eine weitere beliebte Spielart, mit dem Zauberwürfel regelmäßige und unregelmäßige Muster zu erstellen.

Bei vielen Mustern werden nur Würfel der gegenüber liegenden Seiten vertauscht („Pepita-Grundmuster“, „Vierfach Kreuzmuster“, „Sechsfach T-Muster“) bei anderen Mustern nur die Würfel von jeweils drei aneinander liegenden Seiten („Mittelpunkt-Muster“, „Sechsfach Kreuzmuster“, „Würfel-im Würfel“ (auch „2 × 2“ in „3 × 3 × 3“), „Umlaufender Wurm“ / „Schlange“).

Darüber hinaus gibt es farblich gemischte Muster wie den Superflip (alle Kantensteine gekippt) oder eine umlaufende Diagonale durch jeweils zwei farblich unterschiedliche „Dreier-Ecken“.

Prinzipiell sind beim Erstellen von Mustern drei Vorgehensweisen zu unterscheiden:

Muster mit einer speziellen Zugfolge oder einer Kombination mehrerer Zugfolgen erstellen – ausgehend von einem Würfel in Original-Ausgangsstellung mit sechs Farbflächen.
Muster mit einer speziellen Zugfolge oder einer Kombination mehrerer Zugfolgen erstellen – ausgehend von einem bereits in einer Musterstellung gedrehten Würfel („Muster-Wechsel“).
Muster nach Vorlage oder eigener Vorstellung mit den bekannten Zugfolgen erstellen – ausgehend von einem Würfel in Original-Ausgangsstellung mit sechs Farbflächen oder einem zufällig verdrehten Würfel.

Das Phänomen bei einigen erdachten Mustern ist, dass sich bedingt durch die Konstruktion des Würfels nicht alle Muster tatsächlich realisieren lassen. Häufig ist zum Schluss ein Eckwürfel an seiner Position nicht in der richtigen Stellung oder es sind zwei Kantenwürfel an falscher Position (Beispiele: sechsfach umlaufende Diagonale, diverse Pepita-Varianten bei nebeneinander liegenden Seiten). Bei anderen Mustern benötigte man eine andere Kombination der Farbflächen der Eck- oder Kantenwürfel oder ein Kantenwürfel würde doppelt benötigt.

Eine weitere Spielart in diesem Zusammenhang ist es, aus einem im Muster gedrehten Würfel mit nur wenigen Zugfolgen wieder die Original-Ausgangsstellung des Zauberwürfels mit den sechs Farbflächen herzustellen.

Musterbeispiele

Blumenmuster
Schachbrettmuster
erweitertes Schachbrettmuster

Varianten

Es gibt einige Varianten dieses mechanischen Puzzles. Etwas schwieriger ist ein mit Bildern bedruckter Würfel, da durch die allgemein bekannten Lösungsstrategien zwar die Farbflächen an der richtigen Stelle zu liegen kommen, jedoch die mittleren Flächen nicht immer mit der richtigen Orientierung. Beim Rubiks Kalender-Cube (Datumswürfel) sind die Flächen mit Zahlen und Texten versehen, aus denen sich auf der Frontfläche das aktuelle Datum mit Wochentag, Monat und Tag zusammenstellen lässt. Es gibt einfachere Würfel, die aus nur zwei Ebenen in jeder Raumrichtung bestehen wie der Pocket Cube, und kompliziertere Varianten, die aus vier Ebenen (Rubik’s Revenge, auch bekannt als Rubiks Rache beziehungsweise Rubik’s Master Cube), fünf Ebenen (Professor’s Cube oder 5×5×5 Cube bzw. Rubiks Wahn) oder zwei und mehr versetzt ineinander integrierten Würfeln (Rubik’s Fusion) bestehen. Der größte n×n×n massenproduzierte Zauberwürfel ist der 21×21 aus dem Hause MoYu (Stand 2021). Auch gibt es quaderförmige und dodekaederförmige Drehpuzzles. Ferner gibt es Drehpuzzles in Tonnen- oder Pyramidenform und Bälle (Masterball[33]), ebenfalls in verschiedenen Schwierigkeitsstufen. Bereits seit Mitte der 1980er Jahre gibt es den Fisher Cube.

2005 wurde erstmals ein Würfel mit sechs Ebenen präsentiert. Der zugrundeliegende Mechanismus erlaubt auch Würfel mit bis zu elf Ebenen. Diese müssen aber tonnenförmig – die Mitten der Flächen nach außen – verzerrt werden, damit die Befestigung der Ecksteine noch vollständig innerhalb des Würfels liegt. Diese Verzerrung zusammen mit der notwendigen Größe und dem Gewicht werden dem Spieler einiges an Geschick bei der Handhabung abverlangen. Die Lösungsmethoden für diese großen Würfel benötigen keine Züge, die nicht schon vom vier oder fünf Ebenen umfassenden Würfel her bekannt sind.

Seit Juni 2008 sind auch 6×6×6- und 7×7×7-Zauberwürfel auf dem Markt. Mittlerweile gibt es auch größere Zauberwürfel, die offizielle Meisterschaften werden aber seit Februar 2009 nur für maximal 7×7×7-Zauberwürfel ausgetragen.[34][35]

Ein wegen seiner sternförmigen Form sehr beliebtes mechanisches Puzzle ist der 4D8-Zauberwürfel. Diese ist abgeleitet von einem Sterntetraeder, (Stella Octangula) auch Keplerstern genannt. Allerdings sind dabei seine Spitzen abgeschnitten, es verbleiben Pyramidenstümpfe (Truncated Pyramids).

Bei Computerprogrammen, die den Zauberwürfel simulieren, lassen sich auch noch mehr Ebenen einstellen.

Infolge des Booms in den 1980er Jahren tauchten auch mechanische Puzzles auf, denen eine andere Mechanik zu Grunde lag, beispielsweise Rubik’s Magic, die Teufelstonne, Back to Square One, Rubik’s Triamid, Rubik’s Clock, Alexander’s Star oder der Zauberturm. Das mechanisch anspruchsvollste Puzzle dieser Art ist wohl das Dogic in Form eines Ikosaeders (Zwanzigflächner).

Um den Zauberwürfel auch für Blinde und Menschen mit Sehbehinderung zugänglich zu machen, wurden einige haptische Würfel entwickelt. Ein Beispiel hierfür ist der 2010 im Museum of Modern Art präsentierte[36] Braillecube[37], dessen Seiten mit den ersten drei Buchstaben der Farben in Brailleschrift beklebt sind.

Zauberwürfel-Varianten
Zauberwürfel in zufälliger Stellung
Floppycube
Pyraminx
Megaminx
Gigaminx
Teraminx
Sonderform des Zauberwürfels
4D8-Zauberwürfel

Mathematik

Der Würfel als mathematische Gruppe

Der Würfel kann als mathematische Gruppe aufgefasst werden. Dafür wird jede Stellung als eine Verknüpfung der sechs möglichen Basis-Permutationen $B=\{V,H,R,L,O,U\}$ betrachtet. Alle möglichen Permutationen (Stellungen) bilden die Menge $G_{W}$ . Jede Stellung ist durch eine Verknüpfung der sechs Grundpermutationen $B_{W}=\{V,H,R,L,O,U\}\subset G_{W}$ zu erreichen, die mit der zweistelligen Verknüpfung $\circ \colon G\times G\rightarrow G$ verbunden werden.

Außerdem existiert sowohl ein neutrales Element, die Grundstellung $i$ (entspricht einer „Nulloperation“ ausgeführt auf dem gelösten Würfel), denn für alle möglichen Permutationen (Gruppenelemente) $p$ gilt $p\circ i=i\circ p=p$ , als auch ein inverses Element, da zu jeder Permutation $p$ ein Element $p^{-1}$ mit $p\circ p^{-1}=p^{-1}\circ p=i$ existiert, zum Beispiel $R\circ R^{-1}=i$ oder $H^{-2}\circ U^{-1}\circ U\circ H^{2}=i$ . Weiterhin gilt für alle $X\in B_{W}:X^{2}=X^{-2}$ .

Das Tripel $(G,\circ ,i)$ bildet daher eine Gruppe im Sinne der Algebra. Diese ist nicht kommutativ, da die Verknüpfung $\circ$ nicht kommutativ ist: Zum Beispiel gilt $R\circ H\neq H\circ R$ .

Lösungen des Würfels

Sei jetzt eine Permutation $s\in G_{W}$ gegeben (ein verdrehter Würfel), so besteht die Aufgabe darin, eine endliche Folge $(\sigma _{i})$ von Permutationen aus der Menge $B_{W}$ zu finden, die genau diese Permutation $s$ erzeugt:

\sigma _{1}\circ \sigma _{2}\circ \dotsb \circ \sigma _{n}=s

Die Lösung ist nicht eindeutig, das heißt, es gibt viele Lösungen, von denen die kürzeste gesucht ist. Der Durchmesser der Gruppen, also die maximale Länge einer Permutation, mit der alle Elemente aus $G$ erreicht werden, ist für $G_{W}$ 20.

Im Juli 2010 berechneten die drei US-Amerikaner Tomas Rokicki, Morley Davidson und John Dethridge und der Darmstädter Herbert Kociemba, dass jede Stellung in höchstens 20 Zügen (mit Halbdrehungen) gelöst werden kann.[17] Im August 2014 zeigten Tomas Rokicki und Morley Davidson, dass höchstens 26 Züge notwendig sind, wenn als Zug nur Vierteldrehungen erlaubt sind (Halbdrehungen sind dann zwei Züge).[20]

Ordnung der Gruppe G

Die Ordnung einer Gruppe $(G,\circ ,i)$ entspricht der Mächtigkeit ihrer Trägermenge $|G|$ . Da es nur eine endliche Zahl möglicher Stellungen gibt, entspricht diese der Anzahl der möglichen Stellungen:

|G_{W}|

=

{\frac {8!\cdot 3^{8}\cdot 12!\cdot 2^{12}}{3\cdot 2\cdot 2}}=43.252.003.274.489.856.000\approx 4{,}3\cdot 10^{19}

[38]

Diese ergeben sich aus:

8 Positionen, an denen sich die Eckwürfel befinden können. Dabei kann der erste alle 8 Positionen einnehmen, der zweite noch 7 und so weiter, wodurch die Zahl der Kombinationen der Fakultät von 8 entspricht (8!).
3 Orientierungen, die jeder Eckwürfel einnehmen kann (3⁸).
12 Positionen, an denen sich die Kantenwürfel befinden können (12!).
2 Orientierungen, die jede Kante einnehmen kann (2¹²).

Der Nenner ergibt sich aus drei Bedingungen, die gelten, wenn der Würfel verdreht, aber nicht auseinandergenommen wird:

Sieben der acht Eckwürfel lassen sich nach Belieben orientieren, während die Orientierung des achten dadurch erzwungen wird (3).
Elf der zwölf Kantenwürfel lassen sich nach Belieben orientieren, während die Orientierung des zwölften dadurch erzwungen wird (2).
Es lassen sich weder allein zwei Eckwürfel vertauschen, noch lassen sich allein zwei Kanten vertauschen. Die Anzahl der paarweisen Vertauschungen muss immer gerade sein (2).

Untergruppen

Wenn man die Menge der erzeugenden Permutationen begrenzt, entstehen Trägermengen mit geringerer Mächtigkeit, die Teilmengen von $G_{W}$ sind. Diese Untergruppen sind für das Lösen des Würfels mit Computern von entscheidender Bedeutung.

Trivia

Google ehrte den Zauberwürfel anlässlich seines 40. Geburtstags mit einem interaktiven Doodle.[39]
Bei den Simpsons kommt der Zauberwürfel mehrfach vor.[40] Zwei Beispiele, die für die Simpsons nicht glücklich verlaufen: In der Folge Der Ernstfall versucht sich Homer Simpson vor der bevorstehenden Kernschmelze an die Einweisung in sein Schaltpult im Atomkraftwerk zu erinnern. Damals hat er sich anstatt zuzuhören, mit dem Zauberwürfel beschäftigt. In der Episode Der total verrückte Ned holt Marge Simpson den Zauberwürfel heraus, während sich die Familie während eines Hurrikans im Keller aufhält, um sich die Zeit zu vertreiben. Dabei gerät die ganze Familie in einen Streit, so dass Marge enttäuscht den Würfel wieder zurücklegt mit den Worten: „Jetzt weiß ich wieder, warum ich ihn hierher gelegt habe.“
In der 80er Show mit Oliver Geissen ist ein überdimensionales Fragment des Würfels als typisches Symbol der 1980er Jahre Untergestell des Couchtisches, an dem die Gäste und Oliver Geissen sitzen.
In der Sendung Wer wird Millionär? vom 7. Dezember 2015 wurde für eine Million Euro gefragt: „Aus insgesamt wie vielen Steinchen besteht der klassische von Ernő Rubik erfundene Zauberwürfel?“ Der Kandidat Leon Windscheid beantwortete die Frage mit „26“ richtig und wurde somit der zehnte reguläre Millionär der Sendung.[41]
In der Sitcom The Big Bang Theory sieht man gelegentlich einen Papiertuch-Spender in der Form eines übergroßen Zauberwürfels.[42]
Der Künstler Invader bildet Kunstwerke aus Zauberwürfeln nach, etwa die Mona Lisa. Diese wurde im Februar 2020 für 480.000 € versteigert.[43]
In der 4. Staffel von The Last Man on Earth führt das Lösen eines manipulierten Würfels zum unvorhergesehenen Tod eines Kannibalen.

Siehe auch

GNU Gnubik

Literatur

Matthias Stolz: Die Rückkehr des Zaubers. In: Die Zeit, Nr. 4/2009, S. 10–15 (Leben, Über das Comeback des Zauberwürfels, Personen und den Erfinder des Zauberwürfels. Fotos, Interviews).
„Erfreue dich der Symmetrie“. In: Der Spiegel. Nr. 4, 1981 (online).
Schrei Hurra! Schmeiß ’ne Runde! In: Der Spiegel. Nr. 4, 1981 (online – Lösung).

Einführungen und Anleitungen

Wir enträtseln den Zauberwürfel. In: Mathematisches Kabinett. Bild der Wissenschaft. München 1980, November, S. 174–177.
Douglas R. Hofstadter: Vom Zauber des Zauberwürfels. In: Mathematische Spielereien. Spektrum der Wissenschaft. Heidelberg 1981, Mai, S. 16 ff. (Original: Scientific American, März 1981) ISSN 0170-2971 (u. a. Anleitung zur fachgerechten Würfeldemontage, Lösungsstrategie, grafische Muster und Variationen).
Kurt Endl: Rubik’s Rätsel des Jahrhunderts. Würfel-Verlag, Gießen 1981, ISBN 3-923210-15-9.
Josef Trajber: Der Würfel (Rubik’s Cube). Falken, Niedernhausen/Ts. 1981, ISBN 3-8068-0565-2, ISBN 3-8068-0585-7.
Josef Trajber: Der Würfel für Fortgeschrittene. Falken, Niedernhausen/Ts. 1981, ISBN 3-8068-0590-3.
Tom Werneck: Der Zauberwürfel. Heyne, München 1982, ISBN 3-453-41449-7.
Tom Werneck: Der Zauberwürfel für Könner. Heyne, München 1982, ISBN 3-453-41478-0.
Tom Werneck: Die Zauber-Kugel. Vorwort von Martin Gardner. Heyne, München 1982, ISBN 3-453-41505-1 (von Rubik autorisiertes Lösungsbuch).

Mathematik

Die folgenden Titel befassen sich mit den mathematischen Eigenschaften des Zauberwürfels, enthalten aber auch Anleitungen, die u. U. leichter nachzuvollziehen sind als die informellen Einführungen.

David Singmaster: Notes on Rubik’s Magic Cube. Enslow, Hillside NJ 1981. (klassische Studie, die 5. und letzte Auflage hat den doppelten Umfang der ersten aus dem Jahr 1979)
Alexander H. Frey jr., David Singmaster: Handbook of Cubik Math. Enslow, Hillside NJ 1982.
Wolfgang Hintze: Der ungarische Zauberwürfel. Deutscher Verlag der Wissenschaften VEB, Berlin OST 1982 (teilweise angelehnt an Singmasters Buch).
Christoph Bandelow: Einführung in die Cubologie. Vieweg, Braunschweig / Wiesbaden 1981, ISBN 3-528-08499-5.
Christoph Bandelow: Inside Rubik’s Cube and Beyond. Birkhäuser, Basel / Boston 1982. (erweiterte englische Fassung des Vorgenannten)
Ernő Rubik, Tamas Varga, Gerzson Keri, Gyorgy Marx, Tamas Vekerdy: Rubik’s Cubic Compendium. English translation by A. Buvös Kocka, with an afterword by David Singmaster. Oxford University Press, London 1987 (vom Erfinder des Zauberwürfels).
David Joyner: Adventures in Group Theory: Rubik’s Cube, Merlin’s Machine, and Other Mathematical Toys. Johns Hopkins University Press, Baltimore MD 2002 (eine Einführung in die Gruppentheorie anhand des Zauberwürfels).

Weblinks

Commons: Zauberwürfel – Album mit Bildern

Wiktionary: Zauberwürfel – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen

Wikibooks: Zauberwürfel – Lern- und Lehrmaterialien

Weltrekorde mit dem Rubik’s Cube
Literatur zum Thema Zauberwürfel im Katalog der Deutschen Nationalbibliothek
Wie man einen Zauberwürfel (Rubik’s Cube) löst. In: cubesolve.com. Abgerufen am 11. Mai 2021
Rubik’s Cube Löser. Abgerufen am 11. Mai 2021
Wolfgang Blum: Zauberwürfel: Gottes Zahl lautet 20. In: Zeit Online. 10. August 2010; abgerufen am 11. Mai 2021 (Wie viele Züge sind nötig, um jede erdenkliche Kombination zu knacken?).
Julia Könemann: Rubik-Würfel: Alle Stellungen sind in maximal 20 Zügen zu lösen. (mp3-Audio; 2,7 MB; 2:55 Minuten) In: SWR2-Sendung „Impulse“. 10. Mai 2021; abgerufen am 11. Mai 2021.
Julia Könemann: Rubik-Würfel: Alle Stellungen sind in maximal 20 Zügen zu lösen. In: SWR2-Sendung „Impulse“. 10. Mai 2021; abgerufen am 11. Mai 2021.

Einzelnachweise

William Fotheringham: Fotheringham's Sporting Pastimes. Anova Books, 2007, ISBN 1-86105-953-1, S. 50.
Tom de Castella: The people who are still addicted to the Rubik's Cube. In: BBC News Magazine. bbc.com. Abgerufen am 28. April 2014.
Redaktion der Schul-Jugendzeitschrift FLOH (Hrsg.): Hallo Welt – Das große Jugendjahrbuch. Domino Verlag Günther Brinek GmbH, München 1990, S. 48.
Patent HU170062: Térbeli logikai játék. Veröffentlicht am 28. Oktober 1976, Erfinder: Rubik Ernő (https://www.jaapsch.net/puzzles/patents/hu170062.pdf).
Gerichtsurteil zur Patentverletzung auf digital-law-online.info
Gemeinschaftsmarke Nr. 162784, eingetragen am 6. April 1999,
EuG, Urteil vom 25. November 2014 – T-450/09 = GRUR-Prax 2014, 546.
EuGH, Urteil vom 10. November 2016 – C-30/15 P = GRUR 2017, 66 – Simba Toys/EUIPO [Rubik’s Cube].
Annette Kur: „Rubik’s Cube – Würfelzauber am Ende?“. In: GRUR 2017, S. 134–141.
EuG, Urteil vom 24. Oktober 2019 - T-601/17 – Rubik’s Brand / EUIPO
Rubik’s Cube – als Marke entzaubert, in: Rechtslupe.de, 20. November 2019
grafische Notation auf einer Speedcubing-Webseite
Jerry Slocum: The Cube. The Ultimate Guide to the World’s Bestselling Puzzle. Secrets – Stories – Solutions. Black Dog & Leventhal, New York 2009, S. 26.
Korf: Optimal Solutions to Rubik’s Cube. (PDF; 122 kB)
arxiv:0803.3435
Des Würfels letztes Rätsel. In: Der Spiegel. Nr. 23, 2010, S. 103 (online). Homepage von Rokicki
God’s Number is 20 (cube20.org)
Rokicki: Twenty-two moves suffice for Rubik’s cube. (Memento vom 22. Dezember 2008 im Internet Archive) In: Mathematical Intelligencer, 2010, Nr. 1, S. 33
Tomas Rokicki, Herbert Kociemba, Morley Davidson und John Dethridge: The Diameter of the Rubik’s Cube Group Is Twenty. In: SIAM J. Discrete Math., 27(2), 2013, S. 1082–1105, doi:10.1137/120867366
God’s Number is 26 in the Quarter-Turn Metric
Annette Schär: Rubik-Würfel: «Das ist kompliziert, das will ich auch können!» In: Neue Zürcher Zeitung. 10. Juni 2019; abgerufen am 13. Juli 2019 (Der Rubik-Würfel, das Kult-Spielzeug der 1980er Jahre, fasziniert bis heute. In Luzern haben sich über Pfingsten die besten Schweizer Speedcuber in 18 Kategorien gemessen.).
Liste der zukünftigen Competitions auf der Website der WCA
Liste aller Disziplinen und Rekorde auf der Website der World Cube Association
Offizielle WCA-Regeln
http://www.cube20.org/ - Darstellung der Häufigkeiten nach nötigen Schritten zur Lösung
Duncan Geere: Video: CubeStormer II robot beats Rubik’s Cube speed record. In: wired.co.uk. 11. November 2011, archiviert vom Original am 13. November 2011; abgerufen am 20. Mai 2014 (englisch).
The CubeStormer 2 - World Record Rubik’s Cube Solver made from LEGO NXT Mindstorms. In: YouTube. legobuildingblocks, 12. November 2012, abgerufen am 17. März 2014.
Ingo Pakalski: Roboter löst Zauberwürfel schneller als Mensch. Golem.de, 16. März 2014, abgerufen am 17. März 2014.
Henning van Lil: Rekordverdächtiges Drehen am Rubiks Cube: 1,04 Sekunden – der entzauberte Würfel. In: tagesschau.de. Norddeutscher Rundfunk, 28. Januar 2016, abgerufen am 28. Januar 2016.
Jay Flatland, Paul Rose: World’s Fastest Rubik’s Cube Solving Robot. In: youtube.com. 11. Januar 2016, abgerufen am 29. Januar 2016 (englisch).
Roboter mit Infineon-Chip löst Zauberwürfel in Rekordzeit. In: VDI nachrichten Nr. 46, 18. November 2016, S. 2, Rubrik: Diese Woche.
. In: Heise News
lichtsuchender.wordpress.com
Historie der 6×6×6-Zauberwürfel-Rekorde auf der offiziellen World Cube Association Website
Historie der 7×7×7-Zauberwürfel-Rekorde auf der offiziellen World Cube Association Website
Konstantin Datz: Rubik's Cube for the Blind. MoMa, 2010, abgerufen am 21. Juli 2021 (englisch).
Radhika Seth: RUBIK CUBE FOR THE BLIND. Yonko, 17. März 2010, abgerufen am 21. Juli 2021 (englisch).
Rubik’s Cube. Universität Mannheim, Seminar Computeralgebra mit GAP
Das interaktive Google Doodle zum 40. Geburtstag
Der Zauberwürfel bei den Simpsons
mka/dpa: „Wer wird Millionär?“: Student gewinnt die Million – nach 20 Minuten Grübeln. In: spiegel.de. Spiegel Online GmbH, 7. Dezember 2015, abgerufen am 6. Juli 2020.
Screenshot aus The Big Bang Theory
bam/AFP: Mona Lisa aus Zauberwürfeln für 480.000 Euro versteigert. In: spiegel.de. Spiegel Online GmbH, 24. Februar 2020, abgerufen am 5. Juli 2020.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[sporting-1] William Fotheringham: Fotheringham's Sporting Pastimes. Anova Books, 2007, ISBN 1-86105-953-1, S. 50.

[castel-2] Tom de Castella: The people who are still addicted to the Rubik's Cube. In: BBC News Magazine. bbc.com. Abgerufen am 28. April 2014.

[3] Redaktion der Schul-Jugendzeitschrift FLOH (Hrsg.): Hallo Welt – Das große Jugendjahrbuch. Domino Verlag Günther Brinek GmbH, München 1990, S. 48.

[4] Patent HU170062: Térbeli logikai játék. Veröffentlicht am 28. Oktober 1976, Erfinder: Rubik Ernő (https://www.jaapsch.net/puzzles/patents/hu170062.pdf).

[5] Gerichtsurteil zur Patentverletzung auf digital-law-online.info

[6] Gemeinschaftsmarke Nr. 162784, eingetragen am 6. April 1999,

[7] EuG, Urteil vom 25. November 2014 – T-450/09 = GRUR-Prax 2014, 546.

[8] EuGH, Urteil vom 10. November 2016 – C-30/15 P = GRUR 2017, 66 – Simba Toys/EUIPO [Rubik’s Cube].

[9] Annette Kur: „Rubik’s Cube – Würfelzauber am Ende?“. In: GRUR 2017, S. 134–141.

[10] EuG, Urteil vom 24. Oktober 2019 - T-601/17 – Rubik’s Brand / EUIPO

[11] Rubik’s Cube – als Marke entzaubert, in: Rechtslupe.de, 20. November 2019

[12] rafische Notation auf einer Speedcubing-Webseite

[13] Jerry Slocum: The Cube. The Ultimate Guide to the World’s Bestselling Puzzle. Secrets – Stories – Solutions. Black Dog & Leventhal, New York 2009, S. 26.

[14] Korf: Optimal Solutions to Rubik’s Cube. (PDF; 122 kB)

[15] rxiv:0803.3435

[16] Des Würfels letztes Rätsel. In: Der Spiegel. Nr. 23, 2010, S. 103 (online). Homepage von Rokicki

[cube20-17] God’s Number is 20 (cube20.org)

[18] Rokicki: Twenty-two moves suffice for Rubik’s cube. (Memento vom 22. Dezember 2008 im Internet Archive) In: Mathematical Intelligencer, 2010, Nr. 1, S. 33

[19] Tomas Rokicki, Herbert Kociemba, Morley Davidson und John Dethridge: The Diameter of the Rubik’s Cube Group Is Twenty. In: SIAM J. Discrete Math., 27(2), 2013, S. 1082–1105, doi:10.1137/120867366

[cube20qtm-20] God’s Number is 26 in the Quarter-Turn Metric

[21] Annette Schär: Rubik-Würfel: «Das ist kompliziert, das will ich auch können!» In: Neue Zürcher Zeitung. 10. Juni 2019; abgerufen am 13. Juli 2019 (Der Rubik-Würfel, das Kult-Spielzeug der 1980er Jahre, fasziniert bis heute. In Luzern haben sich über Pfingsten die besten Schweizer Speedcuber in 18 Kategorien gemessen.).

[22] Liste der zukünftigen Competitions auf der Website der WCA

[WCA-Rekorde-23] Liste aller Disziplinen und Rekorde auf der Website der World Cube Association

[24] Offizielle WCA-Regeln

[25] ttp://www.cube20.org/ - Darstellung der Häufigkeiten nach nötigen Schritten zur Lösung

[26] Duncan Geere: Video: CubeStormer II robot beats Rubik’s Cube speed record. In: wired.co.uk. 11. November 2011, archiviert vom Original am 13. November 2011; abgerufen am 20. Mai 2014 (englisch).

[27] The CubeStormer 2 - World Record Rubik’s Cube Solver made from LEGO NXT Mindstorms. In: YouTube. legobuildingblocks, 12. November 2012, abgerufen am 17. März 2014.

[28] Ingo Pakalski: Roboter löst Zauberwürfel schneller als Mensch. Golem.de, 16. März 2014, abgerufen am 17. März 2014.

[29] Henning van Lil: Rekordverdächtiges Drehen am Rubiks Cube: 1,04 Sekunden – der entzauberte Würfel. In: tagesschau.de. Norddeutscher Rundfunk, 28. Januar 2016, abgerufen am 28. Januar 2016.

[30] Jay Flatland, Paul Rose: World’s Fastest Rubik’s Cube Solving Robot. In: youtube.com. 11. Januar 2016, abgerufen am 29. Januar 2016 (englisch).

[31] Roboter mit Infineon-Chip löst Zauberwürfel in Rekordzeit. In: VDI nachrichten Nr. 46, 18. November 2016, S. 2, Rubrik: Diese Woche.

[32] . In: Heise News

[33] tsuchender.wordpress.com

[34] Historie der 6×6×6-Zauberwürfel-Rekorde auf der offiziellen World Cube Association Website

[35] Historie der 7×7×7-Zauberwürfel-Rekorde auf der offiziellen World Cube Association Website

[36] Konstantin Datz: Rubik's Cube for the Blind. MoMa, 2010, abgerufen am 21. Juli 2021 (englisch).

[37] Radhika Seth: RUBIK CUBE FOR THE BLIND. Yonko, 17. März 2010, abgerufen am 21. Juli 2021 (englisch).

[38] Rubik’s Cube. Universität Mannheim, Seminar Computeralgebra mit GAP

[39] Das interaktive Google Doodle zum 40. Geburtstag

[40] Der Zauberwürfel bei den Simpsons

[41] /dpa: „Wer wird Millionär?“: Student gewinnt die Million – nach 20 Minuten Grübeln. In: spiegel.de. Spiegel Online GmbH, 7. Dezember 2015, abgerufen am 6. Juli 2020.

[42] Screenshot aus The Big Bang Theory

[43] /AFP: Mona Lisa aus Zauberwürfeln für 480.000 Euro versteigert. In: spiegel.de. Spiegel Online GmbH, 24. Februar 2020, abgerufen am 5. Juli 2020.