Skewb
Der Skewb (Aussprache: [skjuːb]) ist ein würfelförmiges Drehpuzzle im Stil eines Zauberwürfels. Der Skewb ist seit dem 1. Januar 2014 eine Disziplin der World Cube Association (WCA) im Speedcubing, die bei Meisterschaften häufig gespielt wird.

Geschichte und Namensgebung
Der Skewb wurde von dem Londoner Journalisten Tony Durham erfunden[1] und von dem Deutschen Uwe Mèffert vermarktet.[2] Der ursprüngliche Name des Würfels war 1982 zunächst Pyraminx Cube.[3] Dieser Name soll einen Hinweis auf die verwendete Grundmechanik geben und betonen, dass er Teil einer Serie war, zu der auch sein tetraedrisches Puzzle Pyraminx gehört. Der Name „Skewb“ stammt aus einer Abhandlung des amerikanischen Physikers Douglas R. Hofstadter in der Zeitschrift Scientific American aus dem Jahr 1982. Die Wortneuschöpfung „Skewb“ setzt sich aus den englischen Wörtern skew [skjuː] (schief) und cube [kjuːb] (Würfel) zusammen und beschreibt die Form des Puzzles, wie auch die schräge Orientierung der Drehachsen.[4] Mèffert gefiel dieser Name, so dass er diesen für sein Drehpuzzle übernahm.
Beschreibung
Der Skewb hat mit einer Kantenlänge von 55 mm in etwa die gleiche Dimension und die gleiche Grundform wie der original Rubik’s Cube, jedoch verlaufen die Drehachsen nicht wie bei der Konstruktion von Ernő Rubik durch die Flächenmittelpunkte des Würfels, sondern durch die Würfelecken, also entlang der vier Raumdiagonalen des Würfels. Der Würfel ist nur entlang von Ebenen durch die Mitte des Würfels verdrehbar, wobei jede Drehung 120° entspricht. Die Ecken des Würfels lassen sich nicht einzeln verdrehen. Da die Drehebenen durch alle Würfelaußenflächen verlaufen, bedeutet eine Drehung in einer derartigen Ebene eine Veränderung aller sechs Würfelseiten.
Durch die Anordnung der Schnittebenen wird jede Fläche des Würfels in fünf Teile zerlegt, wodurch sich jeweils ein auf der Spitze stehendes, zentrales Quadrat und vier Dreiecke in den Ecken ergeben. Ziel des Drehpuzzles ist, durch Verdrehen zu erreichen, dass jede Würfelfläche nur aus jeweils einer Farbe (Gelb, Orange, Blau, Weiß, Rot beziehungsweise Grün) aufgebaut ist.
Aufbau und Konstruktion
.jpg.webp)
Auf den ersten Blick scheinen die acht Ecken des Skewbs gleichwertig zu sein. Eine genauere Betrachtung zeigt jedoch, dass die Ecken unterschiedlich flexibel auf Druck reagieren. So können die Ecken in zwei Gruppen eingeteilt werden, die jeweils über Flächendiagonalen des Würfels in Verbindung stehen. Direkt nebeneinander liegende Würfelecken gehören also zu verschiedenen Gruppen.
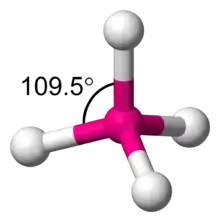
Beim Skewb sind vier der acht Würfelecken im Inneren über Achsen unter einem festen Winkel von 109,5 Grad miteinander zu einem regelmäßigen Tetraeder verbunden.[5] Die relative Position dieser „festen“ Ecken zueinander ist also konstruktionsbedingt immer gleich, wenngleich die Ecken am Ende der Verbindungen selbst um die Drehachse verdreht sein können.[3]
Die anderen vier zwischen den „festen“ Ecken angeordneten „freien“ Ecken sind nicht starr mit dem Zentrum verankert, bilden für sich aber ebenfalls ein regelmäßiges Tetraeder. Auch die relative Position der „freien“ Ecken zueinander ist, abgesehen von einer Verdrehung der Ecken, gleich. Die Orientierung des Tetraeders der „freien“ Ecken im Raum ist jedoch unabhängig von der Orientierung des Tetraeders der „festen“ Ecken, so dass sich die relative Lage einer „freien“ Ecke zu einer „festen“ Ecke durch das Verdrehen ändert. Ein Austausch zwischen beiden Arten von Ecken findet jedoch nicht statt.[3]
Zwischen den Ecken befinden sich sechs quadratische Platten, die ebenfalls nur in die Konstruktion eingeklemmt sind, ohne fest mit dem Zentrum verbunden zu sein. Aufgrund der Freiheitsgrade beim Verdrehen gibt es auch bezüglich dieser Quadrate Einschränkungen. So ist es unmöglich, exakt zwei Quadrate zu vertauschen.[3]
Mathematik und statistische Betrachtung
| n | p |
|---|---|
| 0 | 1 |
| 1 | 8 |
| 2 | 48 |
| 3 | 288 |
| 4 | 1.728 |
| 5 | 10.248 |
| 6 | 59.304 |
| 7 | 315.198 |
| 8 | 1.225.483 |
| 9 | 1.455.856 |
| 10 | 81.028 |
| 11 | 90 |
| Gesamt | 3.149.280 |
Durch die Kopplung der Ecken und die Art der erlaubten Drehungen sind beim Standard-Skewb 3.149.280 verschiedene, unterscheidbare Anordnungen möglich.[3][6] Die im Vergleich zum normalen Zauberwürfel (4 × 1019 Möglichkeiten) deutlich geringere Anzahl von Anordnungen bedeutet jedoch nicht, dass sich die Schwierigkeit, das Drehpuzzle zu lösen, proportional reduziert.[3]
Die Zahl der möglichen Anordnungen ist so gering, dass eine vollständige Simulation von Lösungen mit dem Computer berechnet werden kann. Diese Simulationen zeigen, dass jede Verdrehung des Standard-Skewbs theoretisch in maximal 11 Zügen gelöst werden kann. In der nebenstehenden Tabelle ist die Zahl der minimal benötigten Züge n der Zahl der Permutationen p (unterscheidbare Anordnung) gegenübergestellt.[6]
Durch die Mechanik unterliegen die Orientierung und die Position der Puzzleteile zahlreichen Einschränkungen (siehe oben). Würde man den Würfel in seine Einzelteile zerlegen und ohne Veränderung der Aufkleber wieder willkürlich zusammenbauen, so wären nur etwa 0,02 % aller so erstellten Würfel durch Drehungen lösbar.[7]
Weltrekorde
Seit 2014 werden von der World Cube Association Meisterschaften in der Disziplin Skewb ausgeführt.
Der Geschwindigkeits-Weltrekord im Speedcubing liegt für diesen Würfel (Single Solve) bei 0,93 Sekunden und wurde von Andrew Huang am 12. Juli 2019 bei der WCA World Championship 2019 aufgestellt.[8]
Außerdem gibt es die Disziplin „Average Solve“, bei der ein Teilnehmer fünf Versuche hat und das beste und das schlechteste Ergebnis gestrichen werden und der Durchschnitt der drei übrigen Ergebnisse errechnet wird. Hier liegt der Weltrekord bei 1,86 Sekunden und wurde von Carter Kucala am 4. Dezember 2021 bei der Cubetcha A 2021 aufgestellt.[9]
Varianten des Puzzles
Auch wenn die Außenform der Drehpuzzles sehr unterschiedlich ist, steckt in zahlreichen ein ähnlicher, tetragonaler Grundbaustein. So werden zahlreiche Varianten zur Familie der Skewb-Drehpuzzles gezählt.
 Skewb Ultimate
Skewb Ultimate Skewb Diamond
Skewb Diamond Skewb Kite (Rhombus)
Skewb Kite (Rhombus) Master Skewb
Master Skewb
Einzelnachweise
- David Joyner: Adventures in Group Theory: Rubik's Cube, Merlin's Machine, and Other Mathematical Toys. JHU Press, 2002, ISBN 978-0-8018-6947-1, S. 59 (google.de [abgerufen am 28. Dezember 2018]).
- Uwe Mèffert: The Long History of Pyraminx and its offspring's. 6. November 2017, abgerufen am 28. Dezember 2018 (englisch).
- Douglas Hofstadter: Metamagical Themas: Questing For The Essence Of Mind And Pattern. Basic Books, 2008, ISBN 978-0-7867-2386-7 (google.de [abgerufen am 29. Dezember 2018]).
- Douglas R. Hofstadter: “METAMAGICAL THEMAS: Beyond Rubik’s Cube: spheres, pyramids, dodecahedrons and God knows what else,”. In: Scientific American. Band 247, Nr. 1, Juli 1982, S. 16–31.
- Z3Cubing: Skewb Disassembly and Assembly Tutorial (v2). (Video) In: youtube.com. 24. Mai 2015, abgerufen am 29. Dezember 2018 (englisch).
- Skewb. In: Jaap's Puzzle Page. Jaap Scherphuis, abgerufen am 29. Dezember 2018 (englisch).
- David Joyner: Adventures in Group Theory: Rubik's Cube, Merlin's Machine, and Other Mathematical Toys. JHU Press, 2008, ISBN 978-0-8018-9726-9 (google.de [abgerufen am 30. Dezember 2018]).
- Liste der Skewb Single Weltrekorde auf der Website der World Cube Association
- Liste der Skewb Average Weltrekorde auf der Website der World Cube Association