Weißes Rauschen

Weißes Rauschen ist ein Rauschen mit einem konstanten Leistungsdichtespektrum in einem bestimmten Frequenzbereich. Weißes Rauschen wird als ein stark höhenbetontes Geräusch empfunden (vgl. Psychoakustik). Weißes, in der Bandbreite beschränktes Rauschen wird in den Ingenieur- und Naturwissenschaften häufig verwendet, um Störungen in einem sonst idealen Modell abzubilden, z. B. zufällige Störungen in einem Übertragungskanal zu beschreiben.

Beschreibung

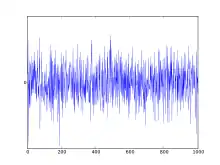
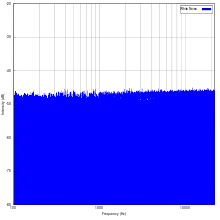
Zeitliche Darstellung eines beispielhaften weißen Rauschsignals

Beispielhaftes Spektrum des weißen Rauschens

Charakteristisch für weißes Rauschen ist ein konstantes Leistungsdichtespektrum:

S(f)={\text{const.}}

Nach dem Wiener-Chintschin-Theorem ist die Autokorrelationsfunktion des weißen Rauschens $\eta (t)$ daher die Delta-Distribution:

r_{\eta \eta }(\tau ):=\operatorname {E} [\eta (t)\eta (t-\tau )]=\int _{-\infty }^{\infty }S(f)e^{\mathrm {j} 2\pi f\tau }df={\text{const}}\cdot \delta (\tau ).

Die Autokorrelationsfunktion von weißem Rauschen ist ein Dirac-Impuls $\delta (\tau ){\overset {t':=t-\tau }{=}}\delta (t-t')$ . Das heißt, das Rauschen zu einem bestimmten Zeitpunkt $t$ ist unkorreliert zu allen anderen Zeitpunkten $t'\neq t$ , da für diese Zeitpunkte die Autokorrelation Null ist.

Weißes Rauschen werden auch zeitdiskrete Signale genannt, deren einzelne Abtastwerte unkorreliert sind.

In der Bandbreite unlimitiertes weißes Rauschen ist ein modellhafter Grenzfall mit unendlich hoher Leistung und tritt daher in der Praxis nicht auf. In realen Systemen tritt weißes Rauschen immer nur in einem Frequenzbereich mit in diesem Bereich konstantem Leistungsdichtespektrum auf. Das Leistungsdichtespektrum außerhalb dieser Bandbreite fällt nach oben hin, bei nur hinreichend hohen Frequenzen, immer gegen 0 ab.

Weißes Rauschen kann mit unterschiedlichen Wahrscheinlichkeitsverteilungen der Signalamplitude auftreten. Eine übliche Verteilung ist die Normalverteilung oder auch Gauß-Verteilung, welche im Rahmen der Signalverarbeitung zur Beschreibung der Störungen von Übertragungskanälen dient. Bei diesen Kanälen wird das Rauschen als additive Störgröße mit eingebracht und dann als additives weißes gaußsches Rauschen bezeichnet. Auch thermisches Rauschen an elektrischen Widerständen lässt sich primär durch weißes gaußsches Rauschen beschreiben. Weißes Rauschen kann grundsätzlich aber auch in anderen Verteilungen auftreten, beispielsweise in Cauchy- oder Poisson-Verteilung.

Anwendungsbereiche

In der Psychoakustik wird weißes Rauschen zur Lärmbekämpfung und im Bereich der Tinnitus-Retraining-Therapie als Masker eingesetzt; Lärm und andere Störgeräusche werden subjektiv als weniger laut und störend empfunden, wenn man sie mit weißem Rauschen überlagert. Rauschen, in dem sich alle Frequenzanteile in etwa gleich laut anhören, wird als 1/f-Rauschen bezeichnet. Es hat ein mit der Frequenz abnehmendes Leistungsdichtespektrum.

In der Stochastik bezeichnet weißes Rauschen einen diskreten stochastischen Prozess von unkorrelierten Zufallsvariablen mit Erwartungswert 0 und konstanter Varianz. Es ist schwach stationär und hat eine konstante Spektraldichte. Das weiße Rauschen stellt den einfachsten stochastischen Prozess dar, jedoch werden viele komplexere Prozesse und Zeitreihen aus solchen konstruiert, etwa der Random Walk oder ARMA-Prozesse.

Farbanalogie des Namens

Der Begriff Weißes Rauschen ist in Analogie zu weißem Licht zu verstehen, in welchem verschiedene optische Frequenzanteile sich zu einem weißen Farbeindruck überlagern. Allerdings weist vom Menschen subjektiv als weiß empfundenes Licht kein konstantes Leistungsdichtespektrum auf.

Mit einer vergleichbaren Farbanalogie wurden die Begriffe Rotes Rauschen und Rosa Rauschen gebildet.

Literatur

Rudolf Müller: Rauschen. 2. Auflage. Springer, 2013, ISBN 978-3-540-51145-8.
Horst Stöcker (Hrsg.): Taschenbuch der Physik. Formeln, Tabellen, Übersichten. 4. Auflage. Harry Deutsch, 2000, ISBN 3-8171-1628-4.
Gopinath Kallianpur: White Noise Theory of Prediction, Filtering and Smoothing. CRC Press Inc., 1988, ISBN 978-2-88124-685-2.

Weblinks

Commons: White noise – Sammlung von Bildern, Videos und Audiodateien

Weißes Rauschen – Rauschspannung in Volt und dB

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.