Vergrößerung (Optik)

Die Vergrößerung eines optischen Instruments ist das Verhältnis zwischen der scheinbaren Größe (Größe des Bilds) und der wahren Größe eines Objekts.

Bei optischen Instrumenten mit Einblick in ein Okular ist unter „Größe“ der Sehwinkel (Betrachtungswinkel) zu verstehen, man spricht dann von Winkelvergrößerung.
Erscheint das Bild auf einem Schirm, ist die „Größe“ ein Längenmaß und kann mit einem Lineal gemessen werden, man spricht dann von linearer Vergrößerung. Die Vergrößerung in Richtung quer zur optischen Achse wird Lateralvergrößerung genannt, die Vergrößerung längs der optischen Achse, die für die Schärfentiefe maßgeblich ist, heißt Axialvergrößerung.

In allen diesen Fällen ist die Vergrößerung eine dimensionslose Zahl, hat also keine physikalische Einheit.

Winkelvergrößerung

Die Vergrößerung $V$ (manchmal auch $\Gamma$ genannt) eines optischen Instruments, in das man mit dem Auge blickt, ist per Definition:

Sehwinkel

V={\frac {\tan \varepsilon }{\tan \varepsilon _{0}}}

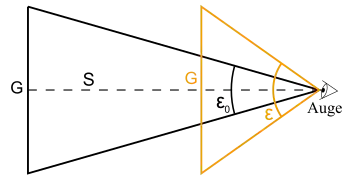
$\varepsilon _{0}$ ist der Sehwinkel, unter dem man einen Gegenstand $G$ ohne optische Hilfsmittel sieht (schwarz gezeichnet). Dieser Winkel hängt vom Abstand $S$ zwischen Auge und Gegenstand ab; je näher der Gegenstand, umso größer der Sehwinkel. Bei Lupen und Mikroskopen wird daher per Konvention ein Abstand von $S:=250\,\mathrm {mm}$ angenommen, in dem man den Gegenstand ohne optische Hilfsmittel noch scharf sehen könnte (deutliche Sehweite).

$\varepsilon$ ist der Sehwinkel, unter dem der Gegenstand im optischen Instrument erscheint (orange gezeichnet). Je größer der Sehwinkel $\varepsilon$ , desto größer sieht das Auge den Gegenstand.

Lupe

Formal errechnet sich die Vergrößerung wie folgt:

V={\frac {\tan \varepsilon }{\tan \varepsilon _{0}}}={\frac {\frac {G}{f}}{\frac {G}{250\,\mathrm {mm} }}}={\frac {250\,\mathrm {mm} }{f}}

wobei 250 mm der Deutlichen Sehweite entspricht und der Gegenstand in der Brennebene liegt.

Mikroskop

Die Vergrößerung eines Mikroskops ist das Produkt aus der Vergrößerung des Objektivs $V_{\mathrm {Ob} }$ und der Vergrößerung des Okulars $V_{\mathrm {Ok} }$ .

V=V_{\mathrm {Ok} }\cdot V_{\mathrm {Ob} }

Die Vergrößerung des Objektivs $V_{Ob}$ errechnet sich aus

V_{\mathrm {Ob} }={\frac {d-f_{\mathrm {Ob} }}{f_{\mathrm {Ob} }}}

,

wobei $f_{\mathrm {Ob} }$ die Brennweite des Objektivs und $d$ der Abstand vom Objektiv zur Brennebene des Okulars ist.
Unter der Vergrößerung des Objektivs wird üblicherweise dessen Abbildungsmaßstab verstanden. Mit der Vergrößerung eines Objektivs ist also keine Winkelvergrößerung gemeint. Vorausgesetzt wird für die Berechnung, dass das Objektiv so eingesetzt wird, wie es im dazugehörenden Mikroskop vorgesehen ist. Das bedeutet, dass der Abstand zum Gegenstand so gewählt wird, dass das Zwischenbild dort entsteht, wo sich im Mikroskop die Brennebene des Okulars befindet (oder in neueren Mikroskopen eine CCD-Kamera). Die Abstände von den zwei Hauptebenen des Okulars zum Gegenstand und zum Zwischenbild sind dabei durch die Linsengleichung festgelegt.
Bei Mikroskopsystemen mit austauschbaren Objektiven wird die Verbindung der Objektive mit dem Mikroskoptubus üblicherweise so angepasst, dass die optische Tubuslänge $t:=d-f_{\mathrm {Ob} }$ , also der Abstand zwischen dem Okular-zugewandten Objektivbrennpunkt und der Zwischenbildebene, für unterschiedliche Objektive konstant bleibt. Dadurch kann die Vergrößerung des Objektivs sehr einfach berechnet werden, nämlich als

V_{\mathrm {Ob} }={\frac {t}{f_{\mathrm {Ob} }}}

Üblich ist eine optische Tubuslänge zwischen $t=160\,\mathrm {mm} {\text{ und }}200\,\mathrm {mm}$ .

Die Vergrößerung des Okulars ist wie die einer Lupe durch

V_{\mathrm {Ok} }={250\,\mathrm {mm} }/f_{\mathrm {Ok} }

gegeben. Genauso wie die Gesamtvergrößerung eines Mikroskops entspricht sie einer Winkelvergrößerung.

Keplersches Fernrohr

Die Vergrößerung eines Fernrohrs (astronomisches Fernrohr oder Feldstecher mit Umkehrprismen) ist durch

V={\frac {f_{\mathrm {Ob} }}{f_{\mathrm {Ok} }}}

gegeben. Dabei sind $f_{\mathrm {Ob} }$ und $f_{\mathrm {Ok} }$ die Brennweiten von Objektiv bzw. Okular.

Um die rechnerische Vergrößerung nutzen zu können, muss aber auch die Öffnung (Objektivdurchmesser, Apertur) und die Austrittspupille des Fernrohrs angemessen gewählt werden:

Zum einen sollte die Austrittspupille des Fernrohrs nicht größer als der Durchmesser der Pupille des Auges sein (2 bis 8 mm, je nach Lichtverhältnissen), da das Auge nur das Licht auswerten kann, das durch die Pupille einfällt.
Da andererseits durch die Vergrößerung der betrachtete Raumwinkel reduziert wird, muss der Objektivdurchmesser entsprechend erhöht werden, damit die gleiche Lichtstärke in das Auge gelangt.

Um gleiche Helligkeit wie beim unvergrößerten Seheindruck zu erhalten, muss also der Objektivdurchmesser in erster Näherung um den Faktor der Vergrößerung größer sein als der Pupillendurchmesser des Auges. Liegt der Objektivdurchmesser unterhalb dieses Wertes, erscheint das vergrößerte Bild dem Betrachter dunkler (und wird damit u. U. nicht mehr gut auswertbar), im umgekehrten Fall ist das vergrößerte Bild heller als das unvergrößerte (und blendet damit u. U. den Betrachter). Letzteren Effekt macht man sich aber – insbesondere in der Astronomie – gerne zunutze um lichtschwache Situationen gut betrachten zu können.

Hohlspiegel

Wird der Hohlspiegel zur Betrachtung des eigenen Spiegelbild, also als Kosmetikspiegel, benutzt, so ist die Vergrößerung gegenüber einem Planspiegel bei gleichem Betrachtungsabstand maximal 2-fach (beide Spiegel im Abstand der Brennweite des Hohlspiegels). Wird der Planspiegel jedoch so nah positioniert, dass das Spiegelbild gerade noch scharf gesehen werden kann, so vergrößert der im Abstand $f$ stehende Hohlspiegel um den Faktor $V=250\,\mathrm {mm} /f$ . Diese Vergrößerung lässt sich durch Verringerung des Abstandes zum Hohlspiegel noch geringfügig steigern.[1]

Grenzen der Vergrößerung

Die Vergrößerung eines optischen Instruments ist zwar theoretisch durch die Wahl der Objektiv- und Okularbrennweiten beliebig steigerbar, allerdings ist das Auflösungsvermögen unter optimalen Bedingungen durch die Beugung des Lichts begrenzt, man spricht von Beugungsbegrenzung. Diese „weiche“ Grenze für die maximal sinnvolle Vergrößerung kann näherungsweise als Durchmesser der Öffnung des Instruments in Millimetern angesetzt werden[2]. Lediglich Vergrößerungen unterhalb dieses Wertes bezeichnet man als nützliche Vergrößerung, da nur innerhalb dieses Bereiches eine Erhöhung der Vergrößerung kleinere Strukturen sichtbar macht. Erhöht man die Vergrößerung über diesen Wert, werden tendenziell keine zusätzlichen Strukturen sichtbar, sondern es entstehen allenfalls Artefakte – so erscheinen z. B. Sterne nicht als Punkte, sondern als Scheibchen, die von konzentrischen Kreisen (Beugungsringen) umgeben sind, man spricht deshalb auch von toter Vergrößerung.

Unter realen Bedingungen begrenzen Abbildungsfehler und bei Fernrohren die Turbulenzen der Luft („Seeing“) die maximal nutzbare Vergrößerung noch weiter. Das Bild kann zwar möglicherweise noch stark vergrößert werden, ohne dass es theoretisch zur Beugungsbegrenzung kommt, es wird dabei jedoch zunehmend unschärfer, die Bildinformation bleibt also trotz stärkerer Vergrößerung praktisch nahezu gleich.

Literatur

Eugene Hecht: Optik. Oldenbourg Verlag, 4. Auflage 2005, ISBN 3-486-27359-0

Einzelnachweise

J. Hattenbach: Die Vergrößerung des eigenen Spiegelbilds im Kosmetikspiegel
Joachim Krautter et al: Meyers Handbuch Weltall, Meyers Lexikonverlag, 7. Auflage 1994, ISBN 3-411-07757-3, S. 553

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] J. Hattenbach: Die Vergrößerung des eigenen Spiegelbilds im Kosmetikspiegel

[2] Joachim Krautter et al: Meyers Handbuch Weltall, Meyers Lexikonverlag, 7. Auflage 1994, ISBN 3-411-07757-3, S. 553