Vakuumpolarisation
Die Vakuumpolarisation ist eine quantenelektrodynamische Erscheinung, die eng mit dem verwandt ist, was in Quantenfeldtheorien allgemein als Vakuumfluktuation bezeichnet wird. Durch Erzeugung und Vernichtung virtueller Teilchen wird dabei das Vakuum zu einem nichtlinear polarisierbaren elektromagnetischen Medium. Obwohl die Vakuumpolarisation nur indirekt als kleine Korrektur in Experimenten beobachtbar ist, bestätigen diese die theoretischen Vorhersagen mit teilweise hoher Genauigkeit. Das durch die Vakuumpolarisation modifizierte elektrische Potential heißt Uehling-Potential.
Grundlagen
Wie in anderen Quantenfeldtheorien mit Wechselwirkung ist auch in der Quantenelektrodynamik das Vakuum definiert als der Zustand mit der niedrigsten möglichen Energie. Der Teilchenzahloperator hat jedoch in diesem Zustand keinen festen Wert, worin sich die Tatsache ausdrückt, dass man das Vakuum nicht als leer auffassen kann. Formal ergibt sich das, weil der Teilchenzahloperator nicht mit dem Hamiltonoperator kommutiert, der die Energie des Vakuumzustands beschreibt.
Obwohl im Vakuum keine reellen, direkt beobachtbaren Teilchen vorhanden sind, hat es doch Eigenschaften, die sich durch eine kurzzeitige, nicht direkt beobachtbare Anwesenheit von Teilchen erklären lassen.[1] Man muss sich bei solchen Beschreibungen jedoch klarmachen, dass sie nur Versuche zur Veranschaulichung formaler theoretischer Sachverhalte sind. Dabei unterliegen die Quantenfelder der Teilchen und daraus gebildete physikalische Messgrößen als Operatoren der heisenbergschen Unschärferelation, d. h. sie können in der Regel keine scharf definierten Erwartungswerte bilden.
Feynman-Diagramme
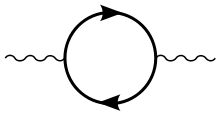
Feynman-Diagramme dienen in der Quantenelektrodynamik zur anschaulichen Darstellung von komplizierten Formeln zur störungstheoretischen Berechnung physikalischer Messgrößen. In der niedrigsten Ordnung wird die Vakuumpolarisation durch ein (virtuelles) Photon beschrieben, das ein (virtuelles) Elektron-Positron-Paar erzeugt, das sich sofort wieder zu einem (virtuellen) Photon vernichtet.
Betrachtet man das Diagramm im Kontext der Streuung zweier geladener Teilchen aneinander, z. B. eines Elektrons im elektromagnetischen Feld eines Atomkerns, so sieht das Elektron bei schwacher Ablenkung, d. h. kleinem Impulsübertrag, eine kleinere, durch die Vakuumpolarisation abgeschirmte elektrische Ladung des Atomkerns als bei starker Ablenkung, d. h. großem Impulsübertrag, wobei es dem Kern viel näher kommt und daher viel weniger von der Abschirmung betroffen ist. Von der klassischen Situation herkommend ist aber gerade die abgeschirmte Ladung in großem Abstand diejenige, die man als klassische Ladung des Atomkerns misst. Daher beschreibt man die Zunahme der Wechselwirkung bei kleineren Abständen durch eine effektive Zunahme der Kopplungskonstanten mit dem Impulsübertrag.[2] Formal ist dasselbe Diagramm auch ein Beitrag zur Selbstenergie des Photons. Sie verschwindet aber für reelle Photonen, was ein Ausdruck dafür ist, dass Photonen masselos sind.
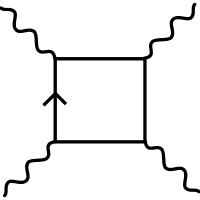
Virtuelle Elektron-Positron-Paare verleihen dem Vakuum Eigenschaften, die in der klassischen Elektrodynamik ein nichtlinear polarisierbares Medium aufwiese. Besonders deutlich wird das in der nächsthöheren nichtverschwindenden Ordnung der Störungstheorie, wo das Feynman-Diagramm für die Vakuumpolarisation vier Photonen an vier Ecken einer geschlossenen Elektron-Positron-Schleife aufweist. Durch dieses Diagramm wird beispielsweise die Photon-Photon-Streuung vorhergesagt, also ein Prozess, bei dem zwei einlaufende elektromagnetische Wellen aneinander gestreut werden. Ein solcher Prozess ist in der (linearen) klassischen Elektrodynamik unmöglich, wo zwei elektromagnetische Wellen sich einfach addieren und daher ohne jede Wechselwirkung durchdringen. Die Wahrscheinlichkeit für den Prozess ist jedoch so klein, dass er bisher nicht nachgewiesen werden konnte. Es gibt jedoch sehr gute Hinweise auf die Photon-Photon-Streuung in den Daten des ATLAS-Experiments bei CERN.[3]
Dasselbe gilt für die Photonspaltung, bei der ein einlaufendes Photon in zwei auslaufende aufgespalten wird, während das vierte Photon im Diagramm als virtuelles Photon die Wechselwirkung mit einem äußeren elektromagnetischen Feld vermittelt, z. B. wieder dem elektromagnetischen Feld eines Atomkerns. Lediglich die Delbrück-Streuung, bei der zwei virtuelle Photonen die Wechselwirkung mit dem elektromagnetischen Feld eines Atomkerns vermitteln, konnte bisher in Übereinstimmung mit der Theorie tatsächlich gemessen werden.
Experimentelle Nachweise
Als gute experimentelle Nachweise der Vakuumpolarisation gelten messbare Beiträge zur Lamb-Verschiebung und zu Teilchenstreuexperimenten.[4] Eine besonders gute Bestätigung liefern die Beiträge der Vakuumpolarisation zum theoretischen Wert des anomalen magnetischen Moments des Elektrons, dessen Präzisionsmessung mit der Theorie verträglich ist. Die Deutung des Casimir-Effekts als Nachweis der Vakuumpolarisation ist umstritten.[5]
In myonischem Wasserstoff ist die Vakuumpolarisation der dominante Beitrag zur Lamb-Verschiebung und hat einen größeren Einfluss als die Feinstruktur.[6]
Literatur
- Claude Itzykson, Jean-Bernard Zuber: Quantum Field Theory. McGraw-Hill, New York, 1980, ISBN 0-07-032071-3
Einzelnachweise
- Eine ausführlichere Veranschaulichung findet man im Kapitel 5 von: Stephen Hawking, Leonard Mlodinow: Der große Entwurf, Rowohlt, Reinbek bei Hamburg, 2010, ISBN 978-3-498-02991-3.
- Eine sehr ausführliche Berechnung dieses Sachverhalts findet man im Kapitel 7-1-1 von: Claude Itzykson, Jean-Bernard Zuber: Quantum Field Theory, McGraw-Hill, New York, 1980, ISBN 0-07-032071-3.
- Evidence for light-by-light scattering in heavy-ion collisions with the ATLAS detector at the LHC, The ATLAS Collaboration, https://arxiv.org/pdf/1702.01625.pdf
- I. Levine, TOPAZ Collaboration: Measurement of the Electromagnetic Coupling at Large Momentum Transfer. In: Physical Review Letters. 78, 1997, S. 424–427. doi:10.1103/PhysRevLett.78.424.
- R. L. Jaffe: The Casimir Effect and the Quantum Vacuum. In: Physical Review D, Band 72, 2005 (Weblink der Cornell University Library)
- R. Pohl: The size of the proton. In: Nature. 466, 2010, S. 213–216. doi:10.1038/nature09250.