Casimir-Effekt
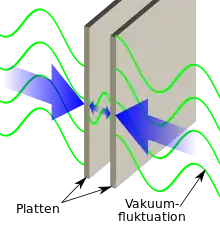
Der Casimir-Effekt ist ein quantentheoretisch deutbarer Effekt der Mikrophysik, der bewirkt, dass auf zwei parallele, leitfähige Platten im Vakuum eine Kraft wirkt, die beide zusammendrückt.[1][2] Der Effekt wurde 1948 durch Hendrik Casimir vorhergesagt und auch nach ihm benannt.[3][4] 1956 erfolgte die experimentelle Bestätigung durch Boris Derjaguin, I. I. Abrikosowa und Jewgeni M. Lifschitz[5] in der Sowjetunion und 1958 durch Marcus Sparnaay von den Philips Forschungslaboratorien in Eindhoven.[6][7]
Wissenschaftler untersuchen die Möglichkeiten, den Casimir-Effekt im Bereich der Nanotechnologie für Mikrosysteme nutzbar zu machen.[8][9][10]
Die Vakuumfluktuation deutet auf eine hypothetische Teilchenklasse hin, die sogenannten virtuellen Teilchen.
Geschichte
Joseph Cugnon berichtet in seinem Artikel[11], wie Casimir zu seiner vereinfachten Berechnung gekommen ist. Die Berechnung von Van-der-Waals-Kräften zwischen Körpern ist sehr aufwändig. Als Casimir nun z. B. für die Van-der-Waals-Kraft zwischen einem Atom und einer leitenden Platte eine unerwartet einfache Formel gefunden hatte, zweifelte er, ob diese stimmen könnte. Er folgte dann einem Ratschlag von Niels Bohr: „Warum berechnen Sie den Effekt nicht, indem Sie die Differenz der Nullpunktenergien des elektromagnetischen Feldes ermitteln?“ Er berechnete daraufhin die Kräfte zwischen zwei Atomen und zwischen einem Atom und einer leitenden Platte. Schließlich wurde ihm klar, dass die Berechnung für zwei leitende Platten noch einfacher ist, und dieses Ergebnis publizierte er schließlich.[12]
Voraussagen der Theorie
Das Ergebnis von Casimir kann über zwei grundlegend verschiedene theoretische Ansätze hergeleitet werden, einen quantenfeldtheoretischen Ansatz, der die Annahme von Vakuumfluktuationen (gleichbedeutend mit einer Nullpunktsenergie des elektromagnetischen Feldes) beinhaltet, und einen Ansatz der klassischen Elektrodynamik. Es besteht nach Cugnon eine „Dualität der physikalischen Interpretation“.[13]
Deutung als Wirkung von Vakuumfluktuationen
Die Casimir-Kraft zwischen leitenden Platten kann berechnet werden, wenn angenommen wird, dass das Vakuum ein Raum voller virtueller Teilchen ist, die als Vakuumfluktuation bezeichnet werden. Solchen Teilchen kann eine De-Broglie-Wellenlänge zugeordnet werden. Außerhalb der Platten sind alle möglichen Wellenlängen zulässig; es existiert ein Kontinuum an virtuellen Teilchen, die jeden beliebigen Impuls
annehmen können (also ein kontinuierliches Spektrum aufweisen) mit
- : reduziertes Plancksches Wirkungsquantum
- : Kreiswellenzahl.
Die Anregungen des diskreten Impulsspektrums lassen sich als stehende Wellen zwischen beiden Platten auffassen. Dabei muss der Abstand der beiden Platten einem Vielfachen der halben Wellenlänge der virtuellen Teilchen entsprechen. Alle anderen Zustände virtueller Teilchen sind dort „verboten“, da sie nicht den Randbedingungen des Wellenfeldes genügen. Von außen stoßen mehr („erlaubte“) virtuelle Teilchen an als im Zwischenraum der Platten, und es entsteht eine Druckdifferenz. Die Teilchen sind virtuell, die Druckdifferenz jedoch real. Dieser Casimir-„Druck“ wirkt als Kraft auf die Platten der jeweiligen Fläche und drückt sie zusammen. Er wird angegeben als „Unterdruck“ (Minuszeichen) zwischen den Platten und beträgt für perfekt leitende Platten im Vakuum:
mit den Größen
- : Kreiszahl
- : reduziertes Plancksches Wirkungsquantum
- : Vakuumlichtgeschwindigkeit
- : Abstand zwischen beiden Platten.
Nach dieser Formel ergibt der Abstand von 190 nm einen Unterdruck von 1 Pa, bei 11 nm erreicht man 100 kPa (1 bar).
Die sehr genaue Übereinstimmung der Messungen mit diesem Ergebnis ist kein Beweis für die Existenz von Vakuumfluktuationen,[14][15] obwohl das einige Physiker behaupten.[16]
Deutung als Van-der-Waals-Kraft zwischen makroskopischen Objekten
Die Casimir-Kraft kann auch gedeutet werden als Summe von Anziehungskräften zwischen Atomen über einen Spalt hinweg (die Wirkung dieser Kräfte ist nicht an das Bestehen eines Vakuums gebunden).
Wechselwirkungen zwischen Atomen/Molekülen (Van-der-Waals-Kräfte) hatte schon Fritz London betrachtet. Casimir und Polder[17] berechneten mit Hilfe retardierter van-der-Waals Potentiale die Kraft, die eine perfekt leitende Platte auf ein einzelnes Atom ausübt, und kamen unter der Verwendung gewisser Näherungen zu einer einfachen Formel. Das wenig später von Casimir veröffentlichte Ergebnis, das über die Annahme von Vakuumfluktuationen zwischen zwei Metallplatten gewonnen wurde, stimmte sehr gut damit überein.
1956 berechnete E. M. Lifschitz[18] in aller Allgemeinheit die Kraft zwischen zwei sich gegenüberstehenden dielektrischen Materieblöcken mit planparallelen Oberflächen.
Die Spezialisierung auf zwei perfekt leitende parallele Metallplatten erbrachte genau das Ergebnis von Casimir.[19]
Also kann der Casimir-Effekt erklärt werden ohne einen Bezug auf Vakuumfluktuationen.[20]
Temperaturabhängigkeit
Brevik, Ellingsen und Milton[21] berechneten mit Hilfe der temperaturabhängigen Greenschen Funktion den Casimir-Effekt für beliebige absolute Temperaturen . Sie fanden für die Anziehungskraft zwischen den Platten pro Fläche (den „Casimir-Druck“) einen analytischen Ausdruck, aus dem sie die Grenzwerte für sehr hohe und sehr niedrige Temperaturen ableiteten[22]:
Hierbei ist ,
- : die Boltzmann-Konstante,
- die absolute Temperatur,
- der Plattenabstand,
- eine numerische Konstante (Zetafunktion für ).
Für große steigt die Anziehungskraft mit der Temperatur linear an, für erhält man das Ergebnis von Casimir.
Für reale Metalle müssen Materialeigenschaften (u. a. endlich große Leitfähigkeit) einbezogen werden und thermodynamische Betrachtungen erfolgen.
Messergebnisse
Quantitative Messungen nahmen Steve Lamoreaux (Seattle, 1997) sowie Umar Mohideen und Anushree Roy (Riverside, 1998) vor.[23]
2009 zeigten Alexej Weber von der Universität Heidelberg und Holger Gies von der Universität Jena, dass der Casimir-Effekt bei gegeneinander gekippten Platten andere Eigenschaften zeigt; so wächst er z. B. mit steigender Temperatur der Oberfläche schneller als im Fall paralleler Platten.[24][25]
Weitere Effekte
Reverser Casimir-Effekt
Es gibt spezielle Fälle, in denen der Casimir-Effekt Abstoßungskräfte zwischen (nicht geladenen) Objekten hervorrufen kann. Dies war bereits 1956 von Jewgeni M. Lifschitz vorhergesagt worden. Die Abstoßungskräfte sollten am leichtesten in Flüssigkeiten auftreten.[26] Nachdem geeignete Metamaterialien vorlagen, wurde der Effekt erneut von Eyal Buks und Michael L. Roukes im Jahr 2002 vorhergesagt.[27] Im Jahre 2007 haben Physiker um Ulf Leonhardt von der Universität St Andrews theoretisch vorhergesagt, dass es unter Zuhilfenahme von Metamaterial mit negativem Brechungsindex möglich wäre, den Casimir-Effekt umzukehren, also eine Abstoßung der Platten zu erreichen. Dies wird reverser oder repulsiver Casimir-Effekt oder auch Quanten-Levitation genannt.[28][29]
Eine experimentelle Demonstration der von Lifschitz vorhergesagten Abstoßung aufgrund der Umkehrung des Casimir-Effektes wurde von Munday et al. 2009 durchgeführt, die den Effekt ebenfalls als Quantenlevitation bezeichneten.[30]
Andere Wissenschaftler haben die Verwendung von laseraktiven Medien zur Erzielung eines ähnlichen Levitationseffekts vorgeschlagen,[31] obwohl dies umstritten ist, da diese Materialien grundlegende Anforderungen an Kausalität und thermodynamisches Gleichgewicht (Kramers-Kronig-Beziehungen) zu verletzen scheinen. Casimir- und Casimir-Polder-Abstoßung kann aber tatsächlich bei ausreichend anisotropen elektrischen Körpern auftreten. Für einen Überblick über die mit der Abstoßung verbundenen Probleme siehe Milton et al.[32] Mehr zum steuerbaren (englisch tunable) abstoßenden Casimir-Effekt siehe Qing-Dong Jiang et al. (2019).[33][34]
Dynamischer Casimir-Effekt
Aus der Quantenfeldtheorie leitete der Physiker Gerald T. Moore 1970 her, dass virtuelle Teilchen, die sich in einem Vakuum befinden, real werden können, wenn sie von einem Spiegel reflektiert werden, der sich fast mit Lichtgeschwindigkeit bewegt. Dieser Effekt wurde später auch dynamischer Casimir-Effekt genannt. Der Experimentalphysiker Per Delsing und Kollegen von der Universität Göteborg konnten diesen Effekt 2011 nachweisen.[35][36][37]
Casimir-Drehmoment
Neben der Casimir-Kraft zwischen parallelen Platten gibt es auch ein Casimir-Drehmoment. Dieses wurde 2018 durch die Verdrehung von Flüssigkristallen nachgewiesen. Die wirkenden Drehmomente lagen in der Größenordnung von einigen milliardstel Newtonmetern.[38]
Sonstiges
Der Casimir-Effekt wurde auch im Breakthrough Propulsion Physics Project der NASA erforscht.[39] Seit 2008 betreibt die DARPA ein Forschungsprogramm, das Casimir Effect Enhancement program.[40]
Literatur
Bücher
- William M. R. Simpson, et al.: Forces of the quantum vacuum - an introduction to Casimir physics. World Scientific, New Jersey 2015, ISBN 978-981-4632-90-4.
- Michael Bordag et al.: Advances in the Casimir effect. Oxford Univ. Pr., Oxford 2009, ISBN 978-0-19-923874-3.
- Kimball A. Milton: The Casimir effect. World Scientific, Singapore 2001, ISBN 981-02-4397-9.
- Vladimir M. Mostepanenko, et al.: The Casimir effect and its applications. Clarendon Press, Oxford 1997, ISBN 0-19-853998-3.
- Frank S. Levin, David A. Micha: Long-range Casimir forces. Plenum Press, New York 1993. ISBN 0-306-44385-6.
Artikel
- Michael Bordag: The Casimir effect 50 years later. In: Proceedings of the 4th Workshop on Quantum Field Theory under the Influence of External Conditions. World Scientific, Singapore 1999, ISBN 981-02-3820-7
- G. Jordan Maclay, (et al.): Of some theoretical significance - implications of Casimir effects. European Journal of Physics, 22, S. 463–469, 2001 Abstract pdf bei arxiv
- Gerold Gründler: Nullpunktsenergie und Casimir-Effekt. Die wesentlichen Argumente für und gegen die Annahme einer physikalisch wirksamen Nullpunktsenergie. Astrophysikalisches Institut Neunhof. Mitteilung sd08011, Februar 2013. Online:
- Christopher Hertlein (et al.): Direct measurement of critical Casimir forces. In: Nature. 451, Nr. 7175, 172–175 (2008) Abstract
- J. N. Munday, F. Capasso, V. A. Parsegian: Measured long-range repulsive Casimir-Lifshitz forces. In: Nature 457, Letter, S. 170–173, 8. Januar 2009 online
- Steven K. Lamoreaux: The Casimir force: background, experiments, and applications. Rep. Prog. Phys., 68 (2005) 201–236, doi:10.1088/0034-4885/68/1/R04, pdf.
Weblinks
- Rainer Scharf: Bisweilen stößt das Nichts auch ab In: Frankfurter Allgemeine Zeitung Nr. 11, 14. Januar 2009, S. N1; online
- Kräfte aus dem Nichts – Presse-Information aus dem Max-Planck-Institut für Metallforschung (2008)
- Eine Kraft aus dem leeren Raum: der Casimir-Effekt – Astronomy Picture of the Day vom 3. Januar 2010.
- Physicists Confirm Power of Nothing, Measuring Force of Universal Flux The New York Times, 21. Januar 1997
- Casimir Introduction@ mit.edu, abgerufen am 12. August 2011
- What is the Casimir effect? @scientificamerican.com
- Astrid Lambrecht: Die Kraft aus dem Nichts. Eine verallgemeinerte Streutheorie auf Basis der Quantenoptik erlaubt es, den Casimir-Effekt für beliebige disjunkte Objekte zu berechnen. In: Physik Journal. Band 15, Nr. 09, 2016, S. 51–55 (pro-physik.de).
- M[arkus] Fierz: Zur Anziehung leitender Ebenen im Vakuum. Cern, Genf 1959. Typo/Manuskript (PDF, 5 Seiten). Online
Video
- Was ist der Casimir-Effekt? aus der Fernseh-Sendereihe alpha-Centauri (ca. 15 Minuten). Erstmals ausgestrahlt am 1. Sep. 2004.
- Der experimentelle Nachweis des Kasimir-Effekts Video-Portrait über Marcus Sparnaay, mit Wolfgang Werner, 2007, ca. 12 min., abgerufen am 28. März 2011
- Peter Milonni: Casimir Effects Colloquium @Institute for Quantum Computing, University of Waterloo, Februar 2011, @youtube, abgerufen am 25. Mai 2012
Einzelnachweise
- Astrid Lambrecht: Das Vakuum kommt zu Kräften: Der Casimir-Effekt. In: Physik in unserer Zeit. 36, Nr. 2, März 2005, S. 85–91. ISSN 1521-3943. doi:10.1002/piuz.200501061. Abgerufen am 28. Juli 2012.
- "The Casimir effect, in its simplest form, is the attraction between two electrically neutral, infinitely large, parallel conducting planes placed in a vacuum" in: Michael Bordag, et al.: Advances in the Casimir effect. Oxford Univ. Pr., Oxford 2009, ISBN 978-0-19-923874-3, S. 1,@google books
- Hendrik Casimir: On the attraction between two perfectly conducting plates. Proc. Kon. Nederland. Akad. Wetensch. B51, 793 (1948) pdf reprint online abgerufen am 12. August 2011
- Diego Dalvit, et al.: Casimir physics. Springer, Berlin 2011, ISBN 978-3-642-20287-2; S. 1ff.: How the Casimir Force was Discovered, @ google books& S. 394ff: The History of Casimir-Polder Experiments., @ google books abgerufen am 19. September 2012
- E.M. Lifshitz: The Theory of Molecular Attractive Forces Between Solids. Soviet Physics 2, 73 (1956), pdf online abgerufen am 12. August 2011
- Experiment with parallel plates by Sparnaay, S. 513–514, Kap.18 General Requirements for Casimir Force measurements, in: Michael Bordag, et al.: Advances in the Casimir effect. Oxford Univ. Pr., Oxford 2009, ISBN 978-0-19-923874-3.
- M.J. Sparnaay: Measurements of attractive forces between flat plates. In: Physica. 24, 1958, S. 751, doi:10.1016/S0031-8914(58)80090-7.
- Federico Capasso, et al.: Attractive and Repulsive Casimir–Lifshitz Forces, QED Torques, and Applications to Nanomachines. S. 249–286, in: Diego Dalvit, et al.: Casimir physics. Springer, Berlin 2011, ISBN 978-3-642-20287-2.
- Federico Capasso, et al.: Casimir forces and quantum electrodynamical torques: physics and nanomechanics. In: IEEE Journal of Selected Topics in Quantum Electronics, Vol.13, issue 2, 2007, S. 400–414, doi:10.1109/JSTQE.2007.893082.
- Metamaterials Could Reduce Friction in Nanomachines sciencedaily.com, abgerufen am 22. November 2012
- Joseph Cugnon: The Casimir Effect and the Vacuum Energy: Duality in the Physical Interpretation. In: Few-Body Systems. 53.1-2 (2012): S. 185. Online:
- H. B. G. Casimir, D. Polder: The Influence of Retardation on the London-van der Waals Forces Phys. Rev. 73, 360 – Veröffentlicht am 15. Februar 1948, doi:10.1103/PhysRev.73.360
- Joseph Cugnon: The Casimir Effect and the Vacuum Energy: Duality in the Physical Interpretation. In: Few-Body Systems. 53.1-2 (2012) (Titel, S. 187), ()
- Gerold Gründler: Nullpunktsenergie und Casimir-Effekt: Die wesentlichen Argumente für und gegen die Annahme einer physikalisch wirksamen Nullpunktsenergie. Astrophysikalisches Institut Neunhof. Mitteilung sd08011, Februar 2013 (PDF; 48 Seiten). Online: Gut erklärender Beitrag auf Lehrbuchniveau. Viele wissenschaftshistorische Details.
- Joseph Cugnon: The Casimir Effect and the Vacuum Energy: Duality in the Physical Interpretation. In: Few-Body Systems. 53.1-2 (2012): S. 187.
- R. L. Jaffe: The Casimir-Effect and the Quantum Vacuum. Online:
- H. B. G. Casimir and D. Polder: The Influence of Retardation on the London-van der Waals forces. Phys. Rev. 73, 360 (Februar 1948)
- E. M. Lifschitz: The Theory of Molecular Attractive Forces between Solids. JETP Vol. 2, Nr. 1, p. 73 (russ. Original: ZhETF Vol. 29, No. 1, p. 94), online
- Formel (4.3) auf Seite 80
- Joseph Cugnon: The Casimir Effect and the Vacuum Energy: Duality in the Physical Interpretation. In: Few-Body Systems. 53.1-2 (2012): S. 187.
- Iver Brevik, Simen A. Ellingsen, Kimball A. Milton: Thermal corrections to the Casimir effect. New Journal of Physics, Vol. 8, Oct. 2006, online
- Die Originalarbeit verwendet Planck-Einheiten ()
- Steve K. Lamoreaux: Demonstration of the Casimir Force in the 0.6 to 6 μm Range. In: Physical Review Lett. Volume 78, 5–8 (1997) Abstract pdf online, abgerufen am 12. August 2011
- Quanteneffekte bei Nanostrukturen In: Spektrum der Wissenschaft, September 2009, S. 12; Interplay between geometry and temperature for inclined Casimir plates, bibcode:2009PhRvD..80f5033W
- Physicists Demonstrate that the Warmer a Surface is, the Stronger its Ability to Attract Nearby Atoms. AZoNano.com, 8. Februar 2007, abgerufen am 21. Juni 2016 (englisch).
- I.E. Dzyaloshinskii, E.M. Lifshitz, L.P. Pitaevskii: The general theory of van der Waals forces. In: Advances in Physics. 10, Nr. 38, 1961, S. 165. bibcode:1961AdPhy..10..165D. doi:10.1080/00018736100101281.
- Eyal Buks, Michael L. Roukes: Quantum physics: Casimir force changes sign. In: Nature. 419, Nr. 6903, 12. September 2002, S. 119–120. ISSN 0028-0836. doi:10.1038/419119a. Abgerufen am 28. Juli 2012.
- Ulf Leonhardt, Thomas G Philbin: Quantum levitation by left-handed metamaterials. In: New Journal of Physics. 9, Nr. 8, 10. August 2007, ISSN 1367-2630, S. 254–254. doi:10.1088/1367-2630/9/8/254. Abgerufen am 28. Juli 2012.
- Ulf Leonhardt: Quantum Levitation, University St. Andrews (via WayBack WebArchiv vom 31. März 2016)
- J. N. Munday, F. Capasso, V. A. Parsegian: Measured long-range repulsive Casimir-Lifshitz forces. In: Nature. 457, Nr. 7226, 2009, S. 170–3. bibcode:2009Natur.457..170M. doi:10.1038/nature07610. PMID 19129843. PMC 4169270 (freier Volltext).
- Roger Highfield: Physicists have 'solved' mystery of levitation. In: The Daily Telegraph, 6. August 2007. Abgerufen am 28. April 2010.
- K. A. Milton, E. K. Abalo, Prachi Parashar, Nima Pourtolami, Iver Brevik, Simen A. Ellingsen: Repulsive Casimir and Casimir-Polder Forces. In: J. Phys. A. 45, Nr. 37, 2012, S. 4006. arxiv:1202.6415. bibcode:2012JPhA...45K4006M. doi:10.1088/1751-8113/45/37/374006.
- Qing-Dong Jiang, Frank Wilczek: Chiral Casimir forces: Repulsive, enhanced, tunable. In: Physical Review B. 99, Nr. 12, 4. März 2019, S. 125403. doi:10.1103/PhysRevB.99.125403.
- Robert Gast: Quantenphysik: Der Casimir-Effekt kann auch anders, auf: Spektrum.de vom 6. März 2019
- Rüdiger Vaas: Von nichts kommt nichts. Januar 2012. Abgerufen im Januar 2017.
- Maike Pollmann: Licht aus Vakuum erzeugt. November 2016. Abgerufen im Januar 2017.
- Gerald T. Moore: Quantum Theory of the Electromagnetic Field in a Variable-Length One-Dimensional Cavity. September 1970, bibcode:1970JMP....11.2679M.
- Jan Oliver Löfken: Virtuelle Photonen verdrehen Flüssigkristall. 11. Januar 2019. Abgerufen am 11. Januar 2019.
- Marc G. Millis: Breakthrough Propulsion Physics Workshop Preliminary Results nasa.gov, (pdf; 821 kB); ASSESSING POTENTIAL PROPULSION BREAKTHROUGHS grc.nasa.gov, abgerufen am 30. August 2012
- Research in a Vacuum - DARPA Tries to Tap Elusive Casimir Effect for Breakthrough Technology scientificamerican.com; DARPA seeks sticky-goldenballs Casimir forcefields theregister.co.uk, abgerufen am 28. März 2011