Pohlsches Rad
Das Pohlsche Rad (nach seinem Erfinder Robert Wichard Pohl) ist ein Drehpendel mit einer variablen Wirbelstrombremse. Es ist horizontal gelagert und wird von einer Spiralfeder in einer Ruhelage gehalten, um die es schwingen kann. Ein an die Feder gekoppelter Erreger mit variabler Amplitude und Frequenz ermöglicht es, erzwungene Schwingungen zu erzeugen.
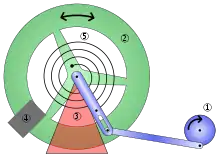

Das Gerät wird zu didaktischen Zwecken eingesetzt, etwa in physikalischen Praktika oder Vorlesungen. Mit ihm werden erzwungene und gedämpfte Schwingungen sowie Resonanzphänomene untersucht.
Spezielle Experimente mit dem Pohlschen Rad
Das Pohlsche Rad und sein Weg ins Chaos
Die Auslenkung des Rades kann man an einer über dem Rad angebrachten Skala ablesen. Damit sich das Pohlsche Rad chaotisch verhält, muss noch in der oberen Hälfte eine Unwucht in Form eines zusätzlichen Gewichtes angebracht werden. Die Dämpfung der Wirbelstrombremse wird auf einen kleinen Wert eingestellt. Das Pendel hat so im unangeregten Zustand zwei stabile Ruhelagen.
Versuchsdurchführung
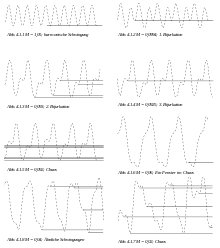
Um den Übergang des Drehpendels zu chaotischem Verhalten zu verdeutlichen, beobachtet man seine Schwingung bei unterschiedlichen Dämpfungsstromstärken und gleichbleibender Erregerfrequenz und -amplitude.
Starke Dämpfung
Man beobachtet, dass das Drehpendel bei hohen Dämpfungsstromstärken nach einer gewissen Einschwingzeit, nämlich so lange, bis Resonanz zwischen Oszillator und Drehpendel besteht, periodisch schwingt. Resonanz bedeutet, dass die Eigenfrequenz des Drehpendels mit der Erregerfrequenz, das heißt zum Beispiel mit der Drehzahl eines die Kurbel antreibenden Elektromotors, übereinstimmt. Wird die Dämpfung verringert, ist eine stetige Vergrößerung der Amplitude zu erwarten.
Mittlere Dämpfung
Bis zu einer gewissen Stärke der Dämpfung ist das auch tatsächlich der Fall. Verringert man sie aber darüber hinaus weiter, kommt es zur Spaltung der Grundamplitude, der so genannten Bifurkation.
Da die Eigenfrequenz des Drehpendels von der Amplitude abhängt, weicht die Schwingungsfrequenz des Drehpendels bei zunehmender Amplitude von der konstanten Anregungsfrequenz ab, sodass keine Resonanz mehr vorliegt, was die Amplitude wiederum verringert. Dadurch gerät das Pendel wieder in Resonanz mit dem Erreger und die Schwingungsamplitude nimmt wieder zu.
Schwache Dämpfung
Bei einer weiteren Verringerung der Dämpfung tritt eine zweite Bifurkation auf. Das heißt, die Grundschwingung ist nun in vier Teilschwingungen aufgeteilt und die Periodenlänge vier Mal so lang. Verringert sich die Dämpfung noch weiter, kommt es zur dritten Bifurkation. Danach ist es sehr schwer, die einzelnen Bifurkationen zu treffen, da die Abstände zwischen ihnen immer kleiner werden. Schließlich stellt sich bei sehr schwacher Dämpfung auch nach langer Einschwingzeit keine periodische Schwingung mehr ein: das Drehpendel schwingt unregelmäßig oder chaotisch.
Fenster im Chaos
Bei einer weiteren Verminderung der Dämpfungsstromstärke ist zu beobachten, dass sich bei bestimmten Dämpfungsstärken plötzlich wieder eine periodische, stabile Schwingung einstellt. Dieses Phänomen wird als Fenster im Chaos bezeichnet. Diese Zustände lösen sich bei einer geringfügigen Veränderung der Dämpfungsstromstärke wieder auf. Diesen Wechsel von Chaos und Ordnung nennt man Intermittenz. Allgemeiner formuliert, ein System verhält sich lange Zeit periodisch, bis es plötzlich chaotisches Verhalten zeigt und dann wieder periodisch wird.
Beschreibung der Drehbewegung im Phasenraum
Bei der Beschreibung der Bewegung des Drehpendels stößt man auf ein Problem, das die Darstellung betrifft. Zur Beschreibung sind drei Größen notwendig: Die Auslenkung φ, die Geschwindigkeit des Pendels ω und die momentane Phase des Oszillators , wobei zwischen 0 und der Periodendauer der Anregung liegt. Mit diesen drei Größen lässt sich die Bewegung des Drehpendels vollständig als Punkt in einem dreidimensionalen Phasenraum beschreiben.
Da ein dreidimensionaler Phasenraum schwierig darzustellen ist, bedient man sich eines Tricks, indem man eine Ebene in den Phasenraum legt, auf der nur die Durchstoßpunkte des dreidimensionalen Schaubilds eingetragen werden. Wählt man diese Ebene günstig, ergibt sich ein leicht darstellbares Schaubild, das die zeitliche Entwicklung des Verhaltens des Systems beschreibt. An der Verteilung der Durchstoßpunkte erkennt man, ob sich das System chaotisch oder periodisch verhält. Bei diesem Versuch tritt deutlich zu Tage, dass bereits kleine Veränderungen in den Anfangsbedingungen große Auswirkungen auf das Endergebnis haben können.
Literatur
- Klaus Lüders, Robert Otto Pohl: Pohls Einführung in die Physik: Band 1: Mechanik, Akustik und Wärmelehre. Springer DE, 17. October 2008, ISBN 978-3-540-76337-6, S. 195ff (Abgerufen am 11 November 2012).
- Hans Joachim Eichler, Heinz-Detlef Kronfeldt, Jürgen Sahm: Das Neue Physikalische Grundpraktikum. Springer DE, 21. September 2005, ISBN 978-3-540-21453-3, S. 75ff (Abgerufen am 11 November 2012).
- Friedhelm Kuypers: Physik für Ingenieure und Naturwissenschaftler. John Wiley & Sons, 4 October 2012, ISBN 978-3-527-66957-8, S. 144ff (Abgerufen am 11. November 2012).
- Ludwig Bergmann, Clemens Schaefer: Lehrbuch Der Experimentalphysik: Mechanik, Relativität, Wärme. Walter de Gruyter, 1998, ISBN 978-3-11-012870-3, S. 654ff (Abgerufen am 11. November 2012).
- Klaus G. Schröder: Schulexperimente zum Chaos am Pohlschen Pendel (Abgerufen am 3. Juli 2013).