Delta T

Als Delta T ( $\Delta T$ ) wird in der Astronomie die Differenz zwischen der Terrestrischen Zeit (TT) und der Universal Time (UT) bezeichnet, also die Differenz zwischen einer absolut gleichmäßig verlaufenden Zeitskala TT, die durch Atomuhren realisiert wird, und der Zeitskala UT, die durch die tatsächliche Erdrotation bestimmt ist:

\Delta T=TT-UT

ΔT im Zeitraum 1657 bis 2018.

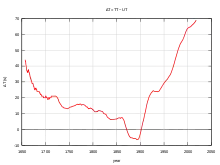
Der aktuelle Wert für $\Delta T$ kann aus den vom International Earth Rotation and Reference Systems Service (IERS) bereitgestellten Daten ermittelt werden. Zu Beginn des 21. Jahrhunderts betrug $\Delta T$ ungefähr 64 Sekunden; bis zum Ende dieses Jahrhunderts könnte der Zeitunterschied auf etwa 204 Sekunden, nach anderen Quellen auf etwa 80 Sekunden anwachsen.[1] Historische Werte für $\Delta T$ lassen sich ungefähr bestimmen, indem überlieferte Beobachtungen mit heutigen Berechnungsergebnissen verglichen werden. Weiterhin gibt es verschiedene aus diesen Daten abgeleitete Polynome zur näherungsweisen Berechnung. Derartige Polynome gibt es auch zur Prognose zukünftiger Werte.

Hintergrund

Aufgrund der Unregelmäßigkeit der Erdrotation ist die Universal Time (UT) kein strikt gleichförmiges Zeitmaß und deshalb für die Ephemeridenrechnung ungeeignet, eignet sich also beispielsweise nicht für die längerfristige Vorausberechnung von Planetenkonstellationen. Auch die aus der Atomzeit abgeleitete Koordinierte Weltzeit (Universal Time Coordinated, UTC) eignet sich nicht, denn bei dieser werden in unregelmäßigen Abständen Schaltsekunden eingefügt, um sie an die Universal Time anzugleichen. Deshalb wurde 1960 die Ephemeridenzeit (ET) eingeführt, die 1984 durch die Terrestrische Dynamische Zeit (TDT) ersetzt wurde, seit 1991 Terrestrische Zeit (TT). Im Gegensatz zu UT und UTC ist TT eine strikt gleichförmige Zeitskala, die Grundeinheit der TT ist die Sekunde (des Internationalen Einheitensystems) und ein Tag ist immer genau 86.400 Sekunden lang.[2]

Der Eintrittszeitpunkt für astronomische Ereignisse wird demzufolge im Regelfall in TT berechnet. Um nun die lokalen Gegebenheiten für die Beobachtung auf der Erdoberfläche angeben zu können, ist allerdings der präzise aktuelle Drehwinkel der Erdrotation zu berücksichtigen. Dies ist beispielsweise bei Sonnenfinsternissen erforderlich, um angeben zu können, welche Orte auf der Erde vom Schatten überstrichen werden. Hierzu muss das in TT vorliegende Berechnungsergebnis in UT bzw. UTC umgerechnet werden, wofür der zu diesem Zeitpunkt prognostizierte Wert für $\Delta T$ zu verwenden ist.

Aktueller Wert und prognostizierte zukünftige Werte

Der aktuelle Wert für $\Delta T$ (Stand Juli 2020) beträgt etwa 69,4 s.[3] Er setzt sich aus drei unterschiedlich schnell variierenden Beiträgen zusammen,

\Delta T=(TT-TAI)+(TAI-UTC)-(UT1-UTC)

.

Der erste Beitrag, die Differenz zwischen TT und der Internationalen Atomzeit TAI, hat den konstanten Wert 32,184 Sekunden.
Der zweite Beitrag, die Differenz zwischen TAI und der Koordinierten Weltzeit UTC, entspricht der Anzahl der bisher bei UTC eingefügten Schaltsekunden (seit dem 1. Januar 2017 37 Sekunden, Stand Juli 2020).
Der letzte Beitrag, die Differenz zwischen der Polschwankungen berücksichtigenden Variante UT1 der Universal Time und UTC, variiert schnell, sein Betrag bleibt aber stets kleiner als 0,9 s. Er ist einer der Erdrotationsparameter, die vom International Earth Rotation and Reference Systems Service (IERS) in seinen Bulletins A und B veröffentlicht werden.[4]

Die folgende Näherungsformel wird für die Berechnung von $\Delta T$ im Zeitraum zwischen 2015 und 3000 verwendet:[5]

\Delta T/\mathrm {s} =67{,}62+0{,}3645\cdot \left(y-2015\right)+0{,}0039755\cdot \left(y-2015\right)^{2}

.

Dabei ist $y$ die Jahreszahl des betrachteten Datums, gegebenenfalls ergänzt um den Jahresbruchteil. Für monatsgenaue Werte setzt man zum Beispiel

y={\text{Jahreszahl}}+{\frac {{\text{Monatsnummer}}-0{,}5}{12}}

.

Historische Werte

Historische Werte von ΔT und ihre Unsicherheit σ[6][7]
Jahr	ΔT (s)	σ (s)	Jahr	ΔT (s)	σ (s)	Jahr	ΔT (s)	σ (s)
−1000	25400	640	1200	740	30	1860	8
−800	22000	550	1400	320	20	1880	−5
−600	18800	460	1600	120	20	1900	−3
−400	15530	390	1700	9	5	1920	21
−200	12790	330	1720	11	3	1940	24
0	10580	260	1740	12	2	1960	33
+200	8640	210	1760	15	2	1980	51
+400	6700	160	1780	17	1	1990	57
+600	4740	120	1800	14	1	2000	64
+800	2960	80	1820	12	1	2010	66
+1000	1570	55	1840	6	<1	2015	68

Historische Werte für $\Delta T$ lassen sich aus dem Vergleich überlieferter Beobachtungen mit modernen Rückrechnungen ermitteln. Brauchbare Beobachtungen gehen etwa bis ins Jahr −700 zurück. Mit der Erfindung des Fernrohrs zu Beginn des 17. Jahrhunderts nahm die Beobachtungsgenauigkeit stark zu, so dass $\Delta T$ sich ab diesem Zeitpunkt deutlich genauer bestimmen lässt.

Literatur

P. Kenneth Seidelmann (Hrsg.): Explanatory Supplement to the Astronomical Almanac. University Science Books, Sausalito 2006, ISBN 1-891389-45-9
F. Richard Stephenson: Historical Eclipses and Earth's Rotation. Cambridge University Press, Cambridge 1997, ISBN 0-521-46194-4

Weblinks

IERS Bulletins. Abgerufen am 8. Januar 2020 (englisch, Bulletin A enthält u. a. den Wert von TT−TAI, die aktuellen Werte von TAI−UTC und UT1−UTC sowie eine Vorhersage von UT1−UTC für die kommenden 12 Monate; wird wöchentlich veröffentlicht.).
Time scales. IERS; abgerufen am 8. Januar 2020 (englisch, Abfrage von aktuellen und früheren Werten von UT1−UTC).
F. Richard Stephenson: Historical eclipses and Earth's rotation. (Memento vom 16. August 2012) Harold Jeffreys Lecture 2002 (PDF; 243 kB)
Fred Espenak: Delta T (ΔT) and Universal Time
R.H. van Gent: Delta T: Terrestrial Time, Universal Time and Algorithms for Historical Periods
F.R. Stephenson, L.V. Morrison, C.Y. Hohenkerk: Measurement of the Earth's Rotation: 720 BC to AD 2015. Proceedings of the Royal Society A, volume 472, issue 2196 (Dez. 2016) (HTML, PDF; 1,4 MB), doi:10.1098/rspa.2016.0404

Einzelnachweise

NASA: Five Millennium Catalog of Solar Eclipses (2001 to 2100) und CalSky
Jean Meeus: The Effect of Delta T on Astronomical Calculations. In: Journal of the British Astronomical Association. 108: 154–156, 1998 (bibcode:1998JBAA..108..154M).
Time scales. IERS, abgerufen am 13. Juli 2020 (englisch).
IERS Bulletins. Abgerufen am 13. Juli 2020.
Fred Espenak: Polynomial Expressions for Delta T.
Morrison L.V., Stephenson F.R.: Historical values of the Earth's clock error ΔT and the calculation of eclipses. Journal for the History of Astronomy, Bd. 35, Teil 3, Nr. 120, S. 327–336 (2004) (bibcode:2004JHA....35..327M); dieselben: Addendum: Historical values of the Earth's clock error. JHA, Bd. 36, Teil 3, Nr. 124, S. 339 (2005) (bibcode:2005JHA....36..339M).
IERS Rapid Service/Prediction Center ().

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] NASA: Five Millennium Catalog of Solar Eclipses (2001 to 2100) und CalSky

[Meeus1998-2] Jean Meeus: The Effect of Delta T on Astronomical Calculations. In: Journal of the British Astronomical Association. 108: 154–156, 1998 (bibcode:1998JBAA..108..154M).

[IERS-UT1-3] Time scales. IERS, abgerufen am 13. Juli 2020 (englisch).

[IERS_Bulletins-4] IERS Bulletins. Abgerufen am 13. Juli 2020.

[Espenak.deltatpoly-5] Fred Espenak: Polynomial Expressions for Delta T.

[6] Morrison L.V., Stephenson F.R.: Historical values of the Earth's clock error ΔT and the calculation of eclipses. Journal for the History of Astronomy, Bd. 35, Teil 3, Nr. 120, S. 327–336 (2004) (bibcode:2004JHA....35..327M); dieselben: Addendum: Historical values of the Earth's clock error. JHA, Bd. 36, Teil 3, Nr. 124, S. 339 (2005) (bibcode:2005JHA....36..339M).

[7] IERS Rapid Service/Prediction Center ().