Spielkreisel

Der Spielkreisel[1] ist in der Kreiseltheorie ein Kreisel, der im Schwerefeld der Erde in keinem Punkt festgehalten auf einem ebenen, waagerechten Untergrund und diesen nur in einem Punkt berührend tanzt, siehe Bild. Von besonderer Bedeutung sind die dargestellten symmetrischen Kreisel, bei denen der Massenmittelpunkt auf der Figurenachse liegt.

Abb. 1: Spielkreisel

Solche Kreisel können Drehungen um die vertikale Figurenachse und reguläre Präzessionen relativ lange ausführen, sofern sie stabil sind. Zwischen den stabilen Lagen streben Kreisel eine von ihnen in einem instationären Ablauf an[2]. Beim schnellen Stehaufkreisel ist die hängende lotrechte Position instabil, die aufrechte stabil und eine reguläre Präzession dazwischen nicht möglich. Deshalb richtet sich dieser Kreisel auf. Die treibende Kraft ist dabei die Reibung am Aufstandspunkt. Die Beschreibung der Bewegungen, Existenz und Stabilität deren Sonderformen, sowie die sie beeinflussenden Reibeffekte sind Gegenstand der Theorie des Spielkreisels.

Über die teils unerwarteten Bewegungen von Spielkreiseln gibt es viele vor allem mathematische Abhandlungen, die zum größten Teil kaum technische Bedeutung beanspruchen können[3]. Das dem Spielkreisel entgegen gebrachte Interesse ist nicht zuletzt

„des eigentümlichen Reizes wegen, den er auf unseren Erkenntnistrieb ausübt.“

– Richard Grammel (1920): [4]

Geschichte

Die wissenschaftliche Behandlung von Kreiseln begann mit J. A. Segner (1704 – 1777), der auch schon die Bedeutung der Reibung für das Aufrichten der Kreiselachse richtig erkannte[5]. Leonhard Euler veröffentlichte 1750 seine Kreiselgleichungen[6] und konnte auch schon Lösungen für den kräftefreien Euler-Kreisel angeben. Joseph-Louis Lagrange leistete 1788 einen wichtigen Beitrag durch Lösung der Gleichungen für den, dem Spielkreisel nahe verwandten, schweren symmetrischen Kreisel mit Stützpunkt[7]. Weitere Sonderfälle der eigentümlichen Bewegungen auf einer Ebene rollender Körper sind von Jean-Baptiste le Rond d’Alembert (1761), Leonhard Euler (1765) und Siméon Denis Poisson (1811) untersucht worden[8].

Die ersten bekannten Versuche das Aufstehen des Wendekreisels zu erklären, stammen von W. Thompson und Prof. Blackburn aus dem 19. Jahrhundert, in dem auch J. H. Jellett (1872)[9] das nach ihm benannte Integral entdeckte. Dass es die Reibungskraft im Aufstandspunkt ist, die den Stehaufkreisel sich aufrichten lässt, erkannten C. M. Braams, N. M. Hugenholtz und W. M. Plisken Anfang der 1950er Jahre. R. J. Cohen formulierte 1977 das heute akzeptierte Modell des Stehaufkreisels und konnte numerisch das Aufstehen des Kreisels simulieren. Zwischen 1994 und 2005 wurde die Kinetik des Spielkreisels weiter aufgeklärt[10].

Beschreibung

Realisierungen und mechanisches Modell

Abb. 2: Kreisel mit Krümmungsradius ρ und -mittelpunkt Z, Massenmittelpunkt G, Aufstandspunkt T, axialem Vektor ê₃ und vertikalem ê_z

Spielkreisel kommen in vielen Formen vor. Eine für gewöhnlich glatte Oberfläche und Rotationssymmetrie wie in Abb. 1 ist nicht nur ästhetisch ansprechend und leicht herzustellen, sondern hält auch den Luftwiderstand gering. Harte und glatte Materialien für Kreisel und Untergrund sorgen für geringe bohrende, Roll- und Gleitreibung.

Je stumpfer die untere Kreiselspitze ist, desto leichter richtet sich der Kreisel auf. Diese Wirkung kehrt sich bei sehr spitzem unterem Kreiselende leicht um, sodass dieselbe Ursache den Kreisel absenkt, siehe Abb. 4. Je spitzer der Kreisel im Aufstandspunkt ist, desto weniger bremst die dort auftretende Reibung, sodass der Kreisel länger tanzt. Die tatsächliche Ausformung bildet einen Kompromiss zwischen diesen widerstreitenden Aspekten.

Der Wendekreisel soll sich aus „hängender“ Position, wo der Massenmittelpunkt unter dem Krümmungszentrum der unteren Kreiselspitze liegt (3/6a in Abb. 3), in aufrechte Lage wenden, wo der Massenmittelpunkt über dem Krümmungszentrum ist (3/6b in Abb. 3). Übliche Ausführungen besitzen einen Stift, auf den sich der Kreisel stellt. Beim Aufrichten passiert er einen kritischen Punkt, wo Stift und kugelförmiger Teil des Kreisels gleichzeitig die Unterlage berühren.

Die inhomogene Kugel mit exzentrischem Massenmittelpunkt wie in Abb. 2[11] ist ein probates Modell eines Kreisels, der keinen kritischen Punkt besitzt. Das Krümmungszentrum der Kreiselspitze ist dann der geometrische Mittelpunkt der Kugel. Beim hängenden Kreisel ist der Massenmittelpunkt unterhalb des geometrischen Mittelpunkts und beim aufrechten Kreisel oberhalb.

Einteilung nach Stabilitätseigenschaften

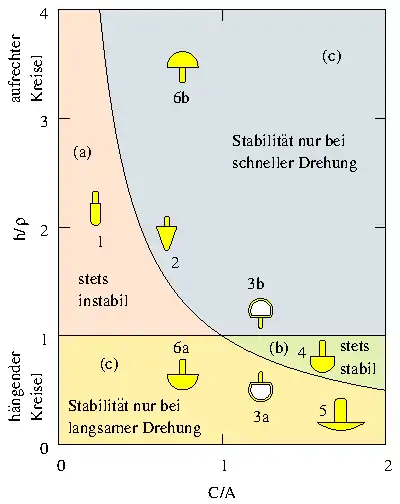
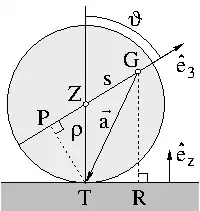
Abb. 3: Stabilitätsdiagramm von Spielkreiseln mit lotrechter Figurenachse

Die Stabilität der Spielkreisel mit lotrechter Figurenachse kann mit der Methode der kleinen Schwingungen von E. Routh[12] untersucht und das Ergebnis graphisch in einem Stabilitätsdiagramm dargestellt werden, siehe Abb. 3[13]. Auf der Abszisse ist das Verhältnis des axialen Hauptträgheitsmoments C zu den äquatorialen Hauptträgheitsmomenten A aufgetragen. Dieses Verhältnis liegt bei einem realen symmetrischen Kreisel im Bereich 0 < C/A < 2. Auf der Ordinate ist das Verhältnis der Höhe h = |GR| des Massenmittelpunkts G über seinem Fußpunkt R auf der Unterlage und dem Krümmungsradius ρ = |ZT| der unteren Kreiselspitze im Aufstandspunkt abgetragen, siehe Abb. 2. Beim aufrecht stehenden Kreisel ist h/ρ > 1, denn mit dem Abstand s = |GZ| zwischen Massenmittelpunkt und Krümmungszentrum ist bei senkrechter Figurenachse h/ρ = (ρ + s)/ρ = 1 + α mit dimensionslosem

α := s/ρ.

Beim lotrecht hängenden Kreisel ist der Massenmittelpunkt unterhalb des Krümmungszentrums, h/ρ = (ρ - s)/ρ = 1 - α, und entsprechend h/ρ < 1. Das Diagramm wird durch die Gerade h/ρ = 1 und die Hyperbel

h/ρ = γ := A/C

in vier unterschiedlich gefärbte Bereiche geteilt.[14]

(a) γ ≥ 1 + α: In diesem Bereich (pink) ist 1 < h/ρ ≤ A/C = γ, sind beim schnellen Kreisel reguläre Präzessionen nur mit Neigungswinkeln ϑ, die cos(ϑ) < ${\tfrac {\alpha }{\gamma -1}}$ erfüllen, möglich und auch stabil, und Drehungen um Vertikalachsen sind stets instabil.
(b) γ ≤ 1 - α: In diesem Bereich (olivgrün) ist γ = A/C ≤ h/ρ < 1, sind beim schnellen Kreisel reguläre Präzessionen im Bereich cos(ϑ) > ${\tfrac {\alpha }{\gamma -1}}$ zwar möglich aber instabil, und die Drehungen um Vertikalachsen sind stets stabil. Dieser Fall wird manchmal indifferent genannt, denn der schnelle Kreisel kann je nach Wunsch so beschleunigt werden, dass er die aufrechte oder die hängende lotrechte Position anstrebt.
(c) 1 - α < γ < 1 + α: In den verbleibenden Bereichen (blaugrau und orange) ist eine reguläre Präzession beim schnellen Kreisel ausgeschlossen, der lotrecht hängende Kreisel nur bei langsamer und der aufrechte nur bei schneller Drehung stabil. Wendekreisel haben dieses Format.

Die Geometrien 3a/b und 6a/b aus dem Bereich (c) sind dem Stehaufkreisel nachempfunden. Wird der Kreisel in lotrecht hängender Lage 3/6a in rasche Drehung versetzt, richtet sich der Kreisel auf, weil seine Stellung instabil ist. Die aufrechten Positionen 3/6b sind beim schnellen Kreisel hingegen stabil. Sofern der Schwung ausreicht, der Kreisel über den kritischen Moment, wo der kugelförmige Teil und der Stift die Unterlage gleichzeitig berühren, hinweg kommt, wird er die aufrechte Stellung erreichen. Der Kreisel 6a kann den kritischen Moment nicht überwinden[15] und ist daher als Stehaufkreisel ungeeignet. Der langsamer werdende Kreisel 3b verlässt die aufrechte Position, sobald diese instabil wird, und strebt die nun stabile hängende Lage 3a an.

Beim nicht so schnellen Kreisel ist die #Stabilität der stationären Bewegungen nicht nur von α und γ, sondern auch vom Schwung, ausgedrückt durch #Jelletts Integral J (die Projektion des Drehimpulses auf die Achse vom Massenmittelpunkt G zum Aufstandspunkt T in Abb. 2), und über den Kreisel eigenen Parameter J_β = ρ√(Csmg) von seiner Gewichtskraft mg abhängig. Die Existenz und Stabilität von stationären Bewegungen wird somit nur von den drei Eigenschaften α, γ und J_β des Kreisels sowie einer Anfangsbedingung J festgelegt.

Vergleich mit dem Lagrange-Kreisel

Der Spielkreisel weist viele Parallelen zum Lagrange-Kreisel auf. Unterschiede ergeben sich daraus, dass sich der Lagrange-Kreisel um den fixierten Aufstandspunkt, der Spielkreisel jedoch um den freien Massenmittelpunkt dreht. Beim Spielkreisel sind die Trägheitsmomente bezüglich des Massenmittelpunkts maßgeblich, die kleiner sind als bei einem baugleichen Lagrange-Kreisel.

Der Spielkreisel ist in lotrecht stehender Lage schon bei kleinerer Drehgeschwindigkeit stabil und ändert seine Neigung unter Einfluss der Reibung deutlich schneller als ein vergleichbarer Lagrange-Kreisel[16]. Der Spielkreisel kann wie der Lagrange-Kreisel eine reguläre Präzession mit den ihr eigenen Merkmalen ausführen. Auch pseudoreguläre Präzessionen sind möglich, wenn der Kreisel sich schnell dreht und der Drehimpuls nahe der Figurenachse ausgerichtet ist. Die pseudoregulären Präzessionen sind bei beiden Kreiseln gleichschnell. Allerdings vollziehen beim Spielkreisel sowohl der Massenmittelpunkt als auch der Aufstandspunkt feine Schwankungen, weswegen von einem Nutationskegel nicht mehr die Rede sein kann[16]. Die Umlaufbahn der unteren Kreiselspitze um die Drehimpulsachse hat beim geneigten Kreisel auch eine vertikale Komponente, mit der sich der Kreisel vom Untergrund abstößt. Bei ausreichendem Schwung kann der Kreisel dabei abheben und auf den Untergrund klopfen.[17]

Für den reibungsfreien Spielkreisel gilt wie beim Lagrange-Kreisel der Satz von Gaston Darboux über homologe Kreisel[18]. Bei beiden Kreiseln sind der Drehimpuls L_z in vertikaler und L₃ in axialer Richtung sowie die im Parameter k enthaltene Gesamtenergie konstant. Die Kreiselfunktion lautet beim Spielkreisel, solange er die Unterlage berührt, mit den Bezeichnungen beim Lagrange-Kreisel:

{\dot {u}}^{2}=U(u)={\frac {(k-L_{3}^{2}-2Ac_{0}u)(1-u^{2})-(L_{z}-L_{3}u)^{2}}{A^{2}{\color {blue}\left(1+{\frac {ms^{2}}{A}}(1-u^{2})\right)}}}

Die Kreiselfunktion des Lagrange-Kreisels (schwarz) bekommt beim Spielkreisel einen zusätzlichen Divisor (blau). Die drei Eulerʹschen Drehwinkel lassen sich mit dieser Kreiselfunktion mit denselben Integralen wie beim Lagrange-Kreisel ausdrücken. Zur graphischen Darstellung der Bewegung wird beim Spielkreisel seine untere Spitze benutzt, deren Bahnlinie in jeder Hinsicht den Locuskurven des Lagrange-Kreisels entspricht[18]. Die analytisch ermittelten Kreiselbewegungen weichen allerdings aufgrund der Reibung im Aufstandspunkt wesentlich von den realen ab.[18]

Kinematik
Herleitung der Kreiselfunktion
Im reibungsfreien Fall hat eine kugelig ausgeformte untere Kreiselspitze keinen Einfluss und kann und soll hier eine ideal spitze Form angenommen werden. Der Massenmittelpunkt liegt im Abstand s vom Aufstandspunkt auf der Figurenachse, die die Neigung ϑ gegenüber der nach oben weisenden Senkrechten hat. Der Massenmittelpunkt befindet sich in der Höhe z = s cos(ϑ) = s u über dem Untergrund, eine kinematische Annahme, die den Kreisel an den Untergrund bindet. Darin ist u = cos(ϑ). Die Zeitableitung davon liefert mit sin²(ϑ) = 1 - u²: ${\dot {u}}=-\sin(\vartheta ){\dot {\vartheta }}\quad \rightarrow \quad {\dot {\vartheta }}^{2}={\frac {{\dot {u}}^{2}}{1-u^{2}}}$ Die Beschleunigung des Massenmittelpunkts ist die zweite Zeitableitung ${\ddot {z}}=s{\ddot {u}}$ .
Impulssatz
Nach dem Impulssatz ergibt sich in Lotrichtung $N-mg=m{\ddot {z}}=ms{\ddot {u}}\rightarrow \;N=mg+ms{\ddot {u}}$ wo N die im Aufstandspunkt senkrecht nach oben wirkende Normalkraft, m die Masse, g die Schwerebeschleunigung und daher mg die Gewichtskraft ist. Der Kreisel hebt nicht ab, solange N > 0 ist, und bei N < 0 würde der Untergrund den Kreisel unrealistisch nach unten ziehen. Eine durch Zeitintegration gefundene Lösung verliert bei N < 0 ihre Gültigkeit und muss darauf hin überprüft werden.
Zerlegung des Drehimpulses
Bei allen symmetrischen Kreiseln gilt mit dem äquatorialen Hauptträgheitsmoment A und dem axialen C die Darstellung ${\vec {\omega }}={\frac {1}{A}}{\vec {L}}+\left({\frac {1}{C}}-{\frac {1}{A}}\right)L_{3}\,{\hat {e}}_{3}$ der Winkelgeschwindigkeit ${\vec {\omega }}$ durch den Drehimpuls ${\vec {L}}$ und seiner Komponente $L_{3}:={\vec {L}}\cdot {\hat {e}}_{3}$ in axialer Richtung ê₃. Die Knotenachse sin(ϑ) ê_N = ê_z × ê₃ stellt die Drehrichtung des Neigungswinkels ϑ der Figurenachse, woraus sich der Drehimpuls L_N in Knotenrichtung ergibt: ${\dot {\vartheta }}={\vec {\omega }}\cdot {\hat {e}}_{N}={\frac {1}{A}}{\vec {L}}\cdot {\hat {e}}_{N}\;\rightarrow \;L_{N}:={\vec {L}}\cdot {\hat {e}}_{N}=A{\dot {\vartheta }}$ In der Präzessionsebene, die senkrecht zur Knotenachse ist und von der Senkrechten ê_z und der Figurenachse ê₃ aufgespannt wird, setzt sich der vertikale Drehimpuls gemäß $L_{z}=L_{3}\cos(\vartheta )+L_{A}\sin(\vartheta )=L_{3}u+L_{A}{\sqrt {1-u^{2}}}$ aus dem axialen Drehimpuls L₃ und einem dazu senkrechten, äquatorialen L_A zusammen.
Drallsatz
Mit dem Drehmoment M_N = s sin(ϑ) N, das die Stützkraft N im horizontalen Abstand s sin(ϑ) vom Massenmittelpunkt ausübt, entsteht aus dem Drallsatz um den Massenmittelpunkt ${\begin{aligned}\qquad {\vec {M}}=&M_{N}\,{\hat {e}}_{N}=s\sin(\vartheta )N\,{\hat {e}}_{N}={\dot {\vec {L}}}\\\rightarrow {\vec {L}}\cdot {\dot {\vec {L}}}=&{\frac {1}{2}}{\frac {\mathrm {d} }{\mathrm {d} t}}({\vec {L}}\cdot {\vec {L}})=s\sin(\vartheta )NL_{N}=s\sin(\vartheta )(mg+ms{\ddot {u}})(A{\dot {\vartheta }})\\=&-A(mgs+ms^{2}{\ddot {u}}){\dot {u}}=-A{\frac {\mathrm {d} }{\mathrm {d} t}}\left(mgs\,u+{\frac {m}{2}}(s{\dot {u}})^{2}\right)\end{aligned}}$ und nach einer Zeitintegration ${\vec {L}}\cdot {\vec {L}}=k-2A\left({\frac {m}{2}}(s{\dot {u}})^{2}+c_{0}u\right)$ wo c₀ = mgs und k eine Integrationskonstante ist. Beim abgehobenen Kreisel tritt kein Moment auf und der Drehimpuls ist konstant, was an dieser Stelle nicht berücksichtigt wird, siehe Impulssatz oben. Mit den vorliegenden Drehimpulskomponenten ergibt sich andererseits ${\vec {L}}\cdot {\vec {L}}=L_{N}^{2}+L_{A}^{2}+L_{3}^{2}=(A{\dot {\vartheta }})^{2}+{\frac {(L_{z}-L_{3}u)^{2}}{1-u^{2}}}+L_{3}^{2}$ Kombination beider Gleichungen für das Drehimpulsquadrat führt mit den kinematischen Zusammenhängen auf die im Text stehende Kreiselfunktion. Die Konstante $k=2AE+\left(1-{\tfrac {A}{C}}\right)L_{3}^{2}$ erscheint auch beim Lagrange-Kreisel, allerdings sind dort die Trägheitsmomente und Drehimpulse bezüglich des Aufstandspunkts maßgeblich und die zur Gesamtenergie E beitragende kinetische Energie bekommt beim Spielkreisel auch einen translatorischen Anteil, siehe #Gesamtenergie des Spielkreisels.

Reibungsbehafteter Spielkreisel

Das Aufrichten des Wendekreisels sogar aus hängender Lage basiert auf Reibeffekten, die also für wesentliche Bewegungsformen des Spielkreisels verantwortlich sind. Bei ausschließlicher Gleitreibung, was in der Kreiseltheorie vorausgesetzt wird, gibt es mit #Jelletts Integral eine Erhaltungsgröße, die durch die Anfangsbedingungen festgelegt ist. An ihnen lässt sich ablesen, wie sich der Kreisel in Zukunft verhalten wird[2]. Der Kreisel kann die lotrechten Positionen hängend oder aufrecht drehend und die reguläre Präzession dauerhaft einnehmen. Dazwischen ist die Bewegung instationär und der Kreisel nähert sich einer stabilen dieser beständigen Drehungen an und verharrt in ihrer Nähe. Allerdings werden stationäre Bewegungen, sofern sie nicht von Anfang an eingestellt werden, wegen der Geschwindigkeitsabhängigkeit der Reibkraft nur asymptotisch erreicht.

Geschwindigkeitsabhängigkeit der Reibkraft

Die untere Kreiselspitze bewegt sich auf dem Untergrund im Allgemeinen mit beachtlichem Schlupf. Die dabei auftretende Gleitreibung erzeugt eine Reibkraft R, die der Geschwindigkeit v des aufstehenden Kreiselpunkts entgegengerichtet ist. Die Reibkraft ist proportional zur Normalkraft N und zum Gleitreibungskoeffizient μ, der im Wesentlichen vom Stoff und der Rauhigkeit der unteren Kreiselspitze sowie des Untergrunds bestimmt wird. Beim Coulombʹschen Reibgesetz ist $R=\mu N$ . Beim Spielkreisel überlagert sich durch die Präzession um die Vertikale eine bohrende Reibung, wodurch sich das Reibgesetz wesentlich verändert:

R=\mu Nv

.

Die Reibkraft wird proportional zur Gleitgeschwindigkeit v. Dieses viskose Reibgesetz wird im Alltag bei einer Bohnermaschine erfahrbar, die mit rotierenden Bürsten arbeitet. Ausgeschaltet ist die Maschine wegen Coulombʹscher Reibung schwerer zu verschieben als bei viskoser Reibung an rotierenden Bürsten[19].

Der qualitative Einfluss der Reibung ist in der Theorie vom Reibgesetz unabhängig, solange die Reibkraft als Funktion der Geschwindigkeit v an der Stelle v = 0 stetig ist und verschwindet.[20]

Einfluss der Reibung

Ohne Reibung kann sich der Kreisel aus folgenden Gründen nicht aufstellen. Im reibungsfreien Fall hat eine Translation des Massenmittelpunkts keinen Einfluss und kann vernachlässigt werden. Der Massenmittelpunkt bewegt sich nur entlang der Senkrechten und die Gesamtenergie, bestehend aus Lageenergie und kinetischer Energie, ist konstant. In lotrechter Position ist die kinetische Energie gleich der Rotationsenergie, die zwischen der hängenden und der aufrechten Lage abnimmt, da der Kreisel Lageenergie gewinnt. Die Rotationsenergie ist in vertikaler Position proportional zum Quadrat des vertikalen Drehimpulses, der demnach beim Aufrichten abnehmen muss. Nach dem Drallsatz bedarf es dazu eines senkrechten Drehmoments, das nur von einer horizontalen Kraft aufgebracht werden kann, und da hier die Reibung die einzige, denkbare, horizontal wirkende Kraft ist, ist sie für das Aufrichten unentbehrlich.[21]

Der dissipative Charakter der Reibung tritt beim sich verlangsamenden Kreisel immer deutlicher hervor:

Bei einer pseudoregulären Präzession erlöschen die Erzitterungen der Figurenachse mit der Zeit.
Je nach Anfangsbedingung und Reibsituation an der unteren Kreiselspitze senkt sich der Kreisel ab oder richtet sich auf und strebt eine stabile stationäre Bewegung in lotrecht stehender oder hängender Position oder in Form einer stabilen regulären Präzession dazwischen an.
In einer solchen Gleichgewichtslage wirken nur noch die bohrende, Roll- und Luftreibung. Fallen diese gering aus, was für gewöhnlich zutrifft und in der Theorie hier voraus gesetzt wird, verharrt der Kreisel relativ lange im eingenommenen Zustand.
Es ist aber nur eine Frage der Zeit, bis sich der langsamer werdende Kreisel absenkt und schließlich lotrecht hängt oder auf dem Weg dorthin auf die Unterlage stößt.
Zuletzt nimmt der Kreisel eine Ruhelage ein.

Nur bei gleitungslosem Abrollen oder Rotation mit senkrechter stillstehender Figurenachse wirkt keine Reibkraft und kann der Kreisel theoretisch dauerhaft tanzen, siehe #Dissipation der Energie durch Reibung. Wenn der Kreisel jedoch gleitet, dann erweckt das eine Reibungskraft, die der Gleitgeschwindigkeit entgegengesetzt ist, die sich aus der Eigendrehung um die Figurenachse und der Präzession derselben um die Vertikale ergibt.

Die Reibkraft wirkt in der Stützebene in doppelter Weise. Erstens beschleunigt sie nach dem Gesetz „Kraft gleich Masse mal Beschleunigung“ den Massenmittelpunkt auch senkrecht zur Figurenachse, die durch das Drehmoment der Gewichtskraft bereits um die Vertikale präzediert. So wird der Massenmittelpunkt im Grundriss momentan in eine Kreisbahn geleitet, siehe Abb. 4[22].

Außerdem erweckt die Reibungskraft ein Reibmoment, dessen Komponente in der Präzessionsebene senkrecht zur Figurenachse den Kreisel aufrichtet oder absenkt[23]. Zu diesem Moment trägt nur der Anteil der Reibkraft bei, der senkrecht zur Figurenachse ist und der wesentlich von der Umfangsgeschwindigkeit v_t des untersten Kreiselpunkts T geprägt wird.

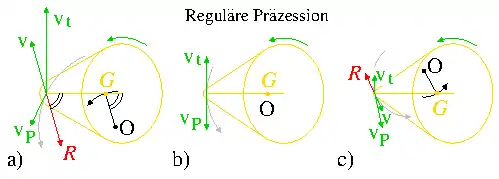
Abb. 4: Spielkreisel (gelb) mit in Bildteilen a, b und c abnehmendem Krümmungsradius ρ der unteren Kreiselspitze.

Abb. 4 zeigt den Grundriss der Bewegung dreier Kreisel mit unterschiedlichen Krümmungsradien der unteren Kreiselspitze. Wird ansonsten nichts verändert, verringert sich mit den Radien vor allem die Umfangsgeschwindigkeit v_t des aufstehenden Punkts T. Die Schwerkraft getriebene Präzessionsgeschwindigkeit und deren Beitrag v_P zur resultierenden Geschwindigkeit v von T bleiben nahezu unberührt. Die Reibkraft R ist der resultierenden Geschwindigkeit v entgegengesetzt, die in Abb. 4a und c umgekehrt orientiert ist und in 4b null ist. In Abb. 4a richtet das Reibmoment den Kreisel auf und in Abb. 4c wird der Kreisel von ihm abgesenkt.[24]

Lagrange-Funktion des Spielkreisels

Die Lagrange-Funktion des Spielkreisels lautet[25]:

{\begin{aligned}{\mathcal {L}}=&{\frac {m}{2}}({\dot {x}}^{2}+{\dot {y}}^{2})+{\frac {1}{2}}[ms^{2}\sin ^{2}(\vartheta )+A]{\dot {\vartheta }}^{2}+{\frac {A}{2}}\sin ^{2}(\vartheta ){\dot {\psi }}^{2}\\&+{\frac {C}{2}}[{\dot {\varphi }}+{\dot {\psi }}\cos(\vartheta )]^{2}-mg[\rho +s\cos(\vartheta )]\end{aligned}}

Darin bedeutet

m die Masse des Kreisels,
${\dot {x}},{\dot {y}}$ die Geschwindigkeiten des Massenmittelpunkts in der horizontalen xy-Ebene,
s der Abstand des Massenmittelpunkts vom Krümmungszentrum der kugelförmigen unteren Kreiselspitze,
ρ der Krümmungsradius dieser Kreiselspitze,
{ψ, ϑ, φ} die Euler-Winkel, und
A, C sind das äquatoriale bzw. das axiale Hauptträgheitsmoment des Kreisels um seinen Massenmittelpunkt.

Die Lagrange-Gleichungen

{\frac {\mathrm {d} }{\mathrm {d} t}}\left({\frac {\partial {\mathcal {L}}}{\partial {\dot {q}}_{i}}}\right)-{\frac {\partial {\mathcal {L}}}{\partial q_{i}}}=Q_{i}

ergeben sich mit den generalisierten Koordinaten q_1,…,5 = x, y, ψ, ϑ, φ und der generalisierten Kraft

Q=\sum _{i=1}^{5}Q_{i}\,\mathrm {d} q_{i}={\vec {R}}\cdot ({\hat {e}}_{x}\,\mathrm {d} x+{\hat {e}}_{y}\,\mathrm {d} y)+({\vec {a}}\times {\vec {R}})\cdot (\,{\hat {e}}_{z}\,\mathrm {d} \psi +{\hat {e}}_{N}\,\mathrm {d} \vartheta +{\hat {e}}_{3}\,\mathrm {d} \varphi )

Wie bei #Jelletts Integral weist ${\vec {a}}$ vom Massenmittelpunkt zum Aufstandspunkt und sin(ϑ) ê_N = ê_z × ê₃ in Knotenrichtung. Die Reibkraft ${\vec {R}}$ wirkt auf der Unterlage, die durch die xy-Ebene repräsentiert wird.

Bewegungsgleichungen

Die Bewegungsgleichungen des Spielkreisels ergeben sich aus dem Impulssatz „Kraft gleich Impulsänderung“, dem Drallsatz „Moment gleich Drehimpulsänderung“ und der Kinematik:[26]

{\begin{aligned}m{\ddot {\vec {G}}}=&(N_{z}-mg)\,{\hat {e}}_{z}+{\vec {R}}\\{\dot {\vec {L}}}=&(-s\,{\hat {e}}_{3}-\rho \,{\hat {e}}_{z})\times (N_{z}\,{\hat {e}}_{z}+{\vec {R}})\\{\dot {\hat {e}}}_{3}=&{\frac {1}{A}}{\vec {L}}\times {\hat {e}}_{3}\\0\leq &w,N_{z},\;wN_{z}=0\end{aligned}}

Darin bedeuten

m die Masse,
${\vec {G}}$ der Massenmittelpunkt (G in Abb. 2),
N_z ≥ 0 die nur bei Kontakt im Aufstandspunkt vorhandene, nie negative, der Gewichtskraft entgegen gerichtete Normalkraft,
g die Schwerebeschleunigung,
ê_z die zur ebenen Unterlage antiparallel zur Gewichtskraft nach oben weisende z-Richtung,
${\vec {R}}$ die bei Kontakt im Aufstandspunkt in der Ebene wirkende Reibkraft,
${\vec {L}}$ der Drehimpuls bezüglich des Massenmittelpunkts,
s der axiale Abstand des Massenmittelpunkts vom Krümmungszentrum (GZ in Abb. 2),
ê₃ der axiale Vektor parallel zur Figurenachse (von Z nach G in Abb. 2),
ρ der Krümmungsradius der halbkugelförmigen unteren Kreiselspitze (ZT in Abb. 2),
A das äquatoriale Hauptträgheitsmoment,
$w:=({\vec {G}}-s\,{\hat {e}}_{3}-\rho \,{\hat {e}}_{z})\cdot {\hat {e}}_{z}\geq 0$ die nie negative Höhe des untersten Kreiselpunkts T über der Unterlage,
der Überpunkt die Zeitableitung, „×“ das Kreuzprodukt und „·“ das Skalarprodukt.

Die Bewegungsgleichungen sind ein System autonomer Differentialgleichungen in neun Variablen ${\vec {G}},\,{\vec {L}},\,{\hat {e}}_{3}$ mit einer Nebenbedingung.

In der dritten Bewegungsgleichung wurde der Zusammenhang zwischen Winkelgeschwindigkeit und Drehimpuls beim symmetrischen Kreisel ausgenutzt[27]:

{\begin{aligned}\quad {\vec {\omega }}=&{\frac {1}{A}}{\vec {L}}+{\frac {A-C}{AC}}L_{3}\,{\hat {e}}_{3}\\\rightarrow \;{\dot {\hat {e}}}_{3}=&{\vec {\omega }}\times {\hat {e}}_{3}={\frac {1}{A}}{\vec {L}}\times {\hat {e}}_{3}\end{aligned}}

Darin ist L₃ der axiale Drehimpuls und C das axiale Hauptträgheitsmoment.

Die letzte der Bewegungsgleichungen verbindet wie eine Komplementaritätsbedingung die nie negative Höhe w des untersten Kreiselpunkts über der Unterlage mit der, nur bei Kontakt auftretenden, senkrechten Kraftkomponente N_z. Sie ergibt sich aus der Konsistenzbedingung ${\ddot {w}}=0$ zu[28]

N_{z}={\frac {mA\left\{g+{\frac {s}{A^{2}}}{\big [}L_{3}L_{z}-({\vec {L}}\cdot {\vec {L}})u{\big ]}\right\}}{A+ms^{2}(1-u^{2})-ms(su+\rho )\,{\hat {e}}_{3}\cdot {\vec {R}}_{1}}}

Darin wurden $u={\hat {e}}_{3}\cdot {\hat {e}}_{z}=\cos(\vartheta ),\,L_{3}={\vec {L}}\cdot {\hat {e}}_{3},\,L_{z}={\vec {L}}\cdot {\hat {e}}_{z}$ und ${\vec {R}}_{1}={\tfrac {1}{N_{z}}}{\vec {R}}$ (μ, N_z, v) eingesetzt, was die Reibkraft aufgrund einer Einheitskraft ist.

Herleitung der Normalkraft N_z
Mit der Winkelgeschwindigkeit ${\vec {\omega }}={\frac {1}{A}}{\vec {L}}+{\frac {A-C}{AC}}L_{3}\,{\hat {e}}_{3}$ werden unter Ausnutzung des Drallsatzes und der Graßmann-Identität die Zeitableitungen der Figurenachse bereit gestellt: ${\begin{aligned}{\dot {\hat {e}}}_{3}=&{\frac {1}{A}}{\vec {L}}\times {\hat {e}}_{3}\\{\ddot {\hat {e}}}_{3}=&{\frac {1}{A}}{\dot {\vec {L}}}\times {\hat {e}}_{3}+{\frac {1}{A}}{\vec {L}}\times {\dot {\hat {e}}}_{3}\\=&{\frac {1}{A}}[(-s\,{\hat {e}}_{3}-\rho \,{\hat {e}}_{z})\times (N_{z}\,{\hat {e}}_{z}+{\vec {R}})]\times {\hat {e}}_{3}+{\frac {1}{A^{2}}}{\vec {L}}\times ({\vec {L}}\times {\hat {e}}_{3})\\=&-{\frac {N_{z}}{A}}[({\vec {R}}_{1}\cdot {\hat {e}}_{3}+u){\vec {a}}+(s+\rho u)({\vec {R}}_{1}+{\hat {e}}_{z})]+{\frac {1}{A^{2}}}[L_{3}{\vec {L}}-({\vec {L}}\cdot {\vec {L}})\,{\hat {e}}_{3}]\end{aligned}}$ Hier wurde ${\vec {R}}=N_{z}{\vec {R}}_{1}$ gesetzt. Mit dem Impulssatz berechnet sich die Beschleunigung des geometrischen Zentrums ${\vec {Z}}:={\vec {G}}-s\,{\hat {e}}_{3}$ (Z in Abb. 2), das den gleichbleibenden Abstand ρ zum untersten Kreiselpunkt hat: ${\begin{aligned}{\ddot {\vec {Z}}}=&{\ddot {\vec {G}}}-s{\ddot {\hat {e}}}_{3}\\=&{\frac {1}{m}}[(N_{z}-mg)\,{\hat {e}}_{z}+{\vec {R}}]-{\frac {s}{A^{2}}}[L_{3}{\vec {L}}-({\vec {L}}\cdot {\vec {L}})\,{\hat {e}}_{3}]\\&+{\frac {sN_{z}}{A}}[({\vec {R}}_{1}\cdot {\hat {e}}_{3}+u){\vec {a}}+(s+\rho u)({\vec {R}}_{1}+{\hat {e}}_{z})]\end{aligned}}$ Beim nicht abgehobenen Kreisel ist die z-Komponente davon 0, was die Bestimmungsgleichung für N_z liefert: ${\begin{aligned}{\ddot {\vec {Z}}}\cdot {\hat {e}}_{z}=&{\frac {1}{m}}(N_{z}-mg)-{\frac {s}{A^{2}}}[L_{3}L_{z}-({\vec {L}}\cdot {\vec {L}})u]\\&+{\frac {sN_{z}}{A}}[-({\vec {R}}_{1}\cdot {\hat {e}}_{3}+u)(\rho +su)+s+\rho u]{\stackrel {!}{=}}0\\\rightarrow N_{z}=&{\frac {g+{\frac {s}{A^{2}}}[L_{3}L_{z}-({\vec {L}}\cdot {\vec {L}})u]}{{\frac {1}{m}}+{\frac {s}{A}}[s+\rho u-({\vec {R}}_{1}\cdot {\hat {e}}_{3}+u)(\rho +su)]}}\end{aligned}}$ Wenige Umformungen führen auf den im Text stehenden Ausdruck.

Jelletts Integral

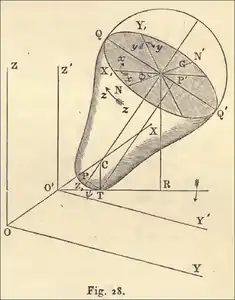
Abb. 5: Symmetrischer Spielkreisel nach Jellett (1872), S. 181.[9]

Bei der Bewegung des Spielkreisels unter ausschließlicher Gleitreibung gibt es eine von J. H. Jellett[9] gefundene und von E. Routh[29] als solche allgemein nachgewiesene Bewegungskonstante

J:={\vec {L}}\cdot {\vec {a}}

Sie ist die Projektion des Drehimpulses ${\vec {L}}$ auf die Verbindungslinie GT = ${\vec {a}}=-s\,{\hat {e}}_{3}-\rho \,{\hat {e}}_{z}$ vom Massenmittelpunkt G zum Aufstandspunkt T an der kugelförmigen unteren Kreiselspitze, siehe Abb. 5 (s = |GC| und ρ = |CT|.)

Jellettʹs Integral ist von der Reibungskraft und somit von den Oberflächeneigenschaften des Untergrunds und des Kreisels unabhängig. Die bohrende, Roll- und Luftreibung, die in der Theorie vernachlässigt werden, zehren realistisch betrachtet die Jellett-Konstante mit der Zeit auf. Die Bedeutung von Jellettʹs Integral fusst darin, dass beim gewöhnlichen Spielkreisel aus Abb. 1 die anderen Reibungsformen wesentlich schwächer ausgeprägt sind als die Gleitreibung.

Bei der regulären Präzession des Spielkreisels ruht der Massenmittelpunkt G und rollt der Kreisel gleitungslos auf dem Untergrund ab. Deshalb ruht der Aufstandspunkt T momentan ebenfalls, denn sonst gäbe es Schlupf. Auch bei der permanenten Drehung um die lotrechte Figurenachse ruhen Massenmittelpunkt und Aufstandspunkt. Bei diesen gleichförmigen Bewegungsformen ist demnach GT = ${\vec {a}}$ die momentane Drehachse. Für die Analyse des Spielkreisels ist daher die folgende Zerlegung des Drehimpulses und der Rotationsenergie zweckmäßig:

{\begin{aligned}{\vec {L}}=:&{\frac {J}{|{\vec {a}}|^{2}\Theta _{a}}}\mathbf {\Theta } \cdot {\vec {a}}+{\vec {L}}_{\bot },\quad {\vec {L}}_{\bot }\cdot {\vec {a}}=0\\E_{\text{rot}}=&{\frac {J^{2}}{2|{\vec {a}}|^{2}\Theta _{a}}}+{\frac {1}{2}}{\vec {L}}_{\bot }\cdot \mathbf {\Theta } ^{-1}\cdot {\vec {L}}_{\bot }\end{aligned}}

Darin ist Θ der Trägheitstensor und Θ_a das bei einer Drehung um GT wirkende Massenträgheitsmoment. Beim Übergang des Kreisels in eine gleichförmige Drehung um GT geht ${\vec {L}}_{\bot }$ gegen null und der Neigungswinkel, der Abstand |GT| sowie das Massenträgheitsmoment Θ_a werden konstant.[30]

Konstanz von Jelletts Integral
Die Zeitableitung der Jellett-Konstante verschwindet bei ausschließlicher Gleitreibung, weil das Moment der Aufstandskraft den axialen Drehimpuls verlustfrei in vertikalen umsetzt und umgekehrt. Denn beim symmetrischen Kreisel sind der Drehimpuls, die Winkelgeschwindigkeit und die Figurenachse komplanar: ${\vec {L}}\cdot ({\vec {\omega }}\times {\hat {e}}_{3})=0$ , siehe Symmetrischer Kreisel#Winkelgeschwindigkeit und Drehimpuls. Die zeitliche Ableitung körperfester Vektoren berechnet sich aus dem Kreuzprodukt mit der Winkelgeschwindigkeit, was insbesondere die Konsequenz ${\vec {L}}\cdot {\dot {\hat {e}}}_{3}={\vec {L}}\cdot ({\vec {\omega }}\times {\hat {e}}_{3})=0$ hat. Nach dem Drallsatz ${\vec {M}}={\dot {\vec {L}}}$ ist die zeitliche Ableitung ${\dot {\vec {L}}}$ des Drehimpulses um den Massenmittelpunkt gleich dem Moment ${\vec {M}}={\vec {a}}\times {\vec {N}}$ , das im Massenmittelpunkt durch die im Aufstandspunkt angreifende Kraft ${\vec {N}}$ aufgebracht wird. Die Kraft muss nicht senkrecht zur Unterlage wirken und beinhaltet ausdrücklich auch etwaige Reibkräfte. Nun ist nach der Produktregel ${\begin{aligned}({\vec {L}}\cdot {\hat {e}}_{3}{\dot {)\;}}=&{\dot {\vec {L}}}\cdot {\hat {e}}_{3}+{\vec {L}}\cdot {\dot {\hat {e}}}_{3}={\vec {M}}\cdot {\hat {e}}_{3}\\=&{\big (}(-s\,{\hat {e}}_{3}-\rho \,{\hat {e}}_{z})\times {\vec {N}}{\big )}\cdot {\hat {e}}_{3}=\rho ({\hat {e}}_{z}\times {\hat {e}}_{3})\cdot {\vec {N}}\end{aligned}}$ wo ausgenutzt wurde, dass im Spatprodukt die Faktoren zyklisch vertauscht werden dürfen. In gleicher Weise zeigt sich ${\begin{aligned}({\vec {L}}\cdot {\hat {e}}_{z}{\dot {)\;}}=&{\dot {\vec {L}}}\cdot {\hat {e}}_{z}={\vec {M}}\cdot {\hat {e}}_{z}\\=&{\big (}(-s\,{\hat {e}}_{3}-\rho \,{\hat {e}}_{z})\times {\vec {N}}{\big )}\cdot {\hat {e}}_{z}=-s({\hat {e}}_{z}\times {\hat {e}}_{3})\cdot {\vec {N}}\end{aligned}}$ Das lässt sich kombinieren zu $0=-s({\vec {L}}\cdot {\hat {e}}_{3}{\dot {)\;}}-\rho ({\vec {L}}\cdot {\hat {e}}_{z}{\dot {)\;}}=[{\vec {L}}\cdot (-s\,{\hat {e}}_{3}-\rho \,{\hat {e}}_{z}){\dot {]\;}}=({\vec {L}}\cdot {\vec {a}}{\dot {)\;}}$ weswegen Jelletts Integral unabhängig von der Aufstandskraft ${\vec {N}}$ und deren Reibanteil eine Konstante liefert.

Näheres zur Zerlegung des Drehimpulses
Der Drehimpuls wird gemäß ${\vec {L}}={\frac {J}{{\vec {a}}\cdot \mathbf {\Theta } \cdot {\vec {a}}}}\mathbf {\Theta } \cdot {\vec {a}}+{\vec {L}}_{\bot }=:{\vec {L}}_{\parallel }+{\vec {L}}_{\bot }$ zerlegt in eine Komponente ${\vec {L}}_{\bot }$ , die wegen ${\vec {a}}\cdot {\vec {L}}_{\bot }={\vec {a}}\cdot {\vec {L}}-{\frac {J}{{\vec {a}}\cdot \mathbf {\Theta } \cdot {\vec {a}}}}{\vec {a}}\cdot \mathbf {\Theta } \cdot {\vec {a}}=0$ senkrecht zu GT ist, und eine Komponente ${\vec {L}}_{\parallel }$ , die, wie sich zeigt, in der Präzessionsebene liegt. Denn jeder axiale Vektor wird durch den Trägheitstensor lediglich mit dem Faktor C und jeder äquatoriale lediglich mit dem Faktor A gestreckt. Somit liegt mit ${\vec {a}}=-s\,{\hat {e}}_{3}-\rho \,{\hat {e}}_{z}$ = GT auch $\mathbf {\Theta } \cdot {\vec {a}}$ in der von ê₃ und ê_z erzeugten Präzessionsebene. Im Allgemeinen ist ${\vec {L}}_{\parallel }\cdot {\vec {L}}_{\bot }\neq 0$ . Die Winkelgeschwindigkeit lautet ${\vec {\omega }}=\mathbf {\Theta } ^{-1}\cdot {\vec {L}}={\frac {J}{{\vec {a}}\cdot \mathbf {\Theta } \cdot {\vec {a}}}}{\vec {a}}+\mathbf {\Theta } ^{-1}\cdot {\vec {L}}_{\bot }$ womit sich die Rotationsenergie um den Massenmittelpunkt berechnet zu ${\begin{aligned}E_{\text{rot}}:=&{\frac {1}{2}}{\vec {\omega }}\cdot {\vec {L}}={\frac {J}{2{\vec {a}}\cdot \mathbf {\Theta } \cdot {\vec {a}}}}\underbrace {\overbrace {{\vec {\omega }}\cdot \mathbf {\Theta } } ^{\vec {L}}\cdot {\vec {a}}} _{J}+{\frac {1}{2}}\left({\frac {J}{{\vec {a}}\cdot \mathbf {\Theta } \cdot {\vec {a}}}}{\vec {a}}+\mathbf {\Theta } ^{-1}\cdot {\vec {L}}_{\bot }\right)\cdot {\vec {L}}_{\bot }\\=&{\frac {J^{2}}{2\|{\vec {a}}\|^{2}\Theta _{a}}}+{\frac {1}{2}}{\vec {L}}_{\bot }\cdot \mathbf {\Theta } ^{-1}\cdot {\vec {L}}_{\bot }\end{aligned}}$ Durch algebraische Umformungen kann weiters ${\begin{aligned}\|{\vec {a}}\|=&\rho {\sqrt {(\alpha +u)^{2}+1-u^{2}}}\\\Theta _{a}:=&{\frac {{\vec {a}}\cdot \mathbf {\Theta } \cdot {\vec {a}}}{\|{\vec {a}}\|^{2}}}={\frac {(\alpha +u)^{2}+\gamma (1-u^{2})}{(\alpha +u)^{2}+1-u^{2}}}C\end{aligned}}$ nachgewiesen werden. Darin ist α = s/ρ, γ = A/C und u = cos(ϑ) der Cosinus des Neigungswinkels ϑ des Kreisels.

Reguläre Präzession

Bei der regulären Präzession ruht der Massenmittelpunkt[31] und sind die Winkelgeschwindigkeiten um die Lotrichtung und Figurenachse sowie die Neigung der Figurenachse konstant. Beim reibungsbehafteten Spielkreisel findet nur dann keine #Dissipation der Energie durch Reibung statt, wenn die untere Kreiselspitze auf dem Untergrund gleitungslos abrollt. Dazu müssen Präzessionsgeschwindigkeit, Eigendrehung und Neigung aufeinander abgestimmt sein. Aus der Bedingung an den Drehimpuls bei der regulären Präzession L_f L_v = Amgs resultiert die Präzessionsgeschwindigkeit

{\dot {\psi }}={\sqrt {\frac {mgs}{C[\alpha +(1-\gamma )u]}}}

Damit eine reguläre Präzession stattfinden kann, muss der Ausdruck in der eckigen Klammer im Nenner positiv sein. Wegen der Rollbedingung gibt es, anders als im reibungsfreien Fall, zu jedem Neigungswinkel höchstens eine Präzessionsgeschwindigkeit.

Der Betrag von #Jelletts Integral nimmt die Form[32]

J_{R}(u)=J_{\beta }{\frac {(\alpha +u)^{2}+\gamma (1-u^{2})}{\sqrt {\alpha +(1-\gamma )u}}}

an, worin J_β = ρ√(Cmgs) eine Kreisel eigene Konstante mit der Dimension des Jellett-Integrals ist.

Ruhbedingung des Aufstandspunkts
Herleitung der Präzessionsgeschwindigkeit
Die mit den Eulerʹschen Winkeln ψ, ϑ und φ ausgedrückten Winkelgeschwindigkeiten p, q, r = ω_1,2,3 und Hauptachsen ê_1,2,3, siehe Kreiseltheorie#Bezugssysteme und Euler-Winkel, liefern bei ruhendem Aufstandspunkt ( ${\dot {\varphi }}=\alpha {\dot {\psi }}$ siehe unten): ${\begin{aligned}L_{z}:=&{\vec {L}}\cdot {\hat {e}}_{z}=Ap\sin(\vartheta )\sin(\varphi )+Aq\sin(\vartheta )\cos(\varphi )+Cr\cos(\vartheta )\\=&{\big (}A\sin ^{2}(\vartheta )+C\cos ^{2}(\vartheta ){\big )}{\dot {\psi }}+C\cos(\vartheta ){\dot {\varphi }}\\L_{3}:=&{\vec {L}}\cdot {\hat {e}}_{3}=Cr=C{\big (}{\dot {\psi }}\cos(\vartheta )+{\dot {\varphi }}{\big )}\\{\vec {L}}=&L_{v}{\hat {e}}_{z}+L_{f}{\hat {e}}_{3}\\L_{v}=&{\frac {L_{z}-L_{3}\cos(\vartheta )}{\sin ^{2}(\vartheta )}}=A{\dot {\psi }}\\L_{f}=&{\frac {L_{3}-L_{z}\cos(\vartheta )}{\sin ^{2}(\vartheta )}}=C[\alpha +(1-\gamma )\cos(\vartheta )]{\dot {\psi }}\end{aligned}}$ Die Bedingung an den Drehimpuls bei der regulären Präzession L_f L_v = Amgs liefert schließlich die im Text angegebene Präzessionsgeschwindigeit ${\dot {\psi }}={\sqrt {\frac {mgs}{C[\alpha +(1-\gamma )u]}}}$
Der Massenmittelpunkt G wird mit dem Vektor ${\vec {G}}$ identifiziert und genauso der unterste Kreiselpunkt T mit ${\vec {T}}={\vec {G}}+{\vec {a}}$ , wobei der Vektor ${\vec {a}}=-s\,{\hat {e}}_{3}-\rho \,{\hat {e}}_{z}$ von G nach T körperfest ist. Die Geschwindigkeit von T lautet demnach ${\dot {\vec {T}}}={\dot {\vec {G}}}+{\vec {\omega }}\times {\vec {a}}={\dot {\vec {G}}}-{\vec {\omega }}\times (s\,{\hat {e}}_{3}+\rho \,{\hat {e}}_{z})$ Bei der regulären Präzession ist die Winkelgeschwindigkeit parallel zu GT ( ${\vec {\omega }}\times {\vec {a}}={\vec {0}}$ ) und ruht T, weswegen der Massenmittelpunkt stillsteht. Die Winkelgeschwindigkeit kann mit den Eulerʹschen Winkeln ψ, ϑ und φ im Eulerʹschen Basissystem ausgedrückt werden: ${\vec {\omega }}={\dot {\psi }}\,{\hat {e}}_{z}+{\dot {\vartheta }}\,{\hat {e}}_{N}+{\dot {\varphi }}\,{\hat {e}}_{3}$ , worin der Vektor $\sin(\vartheta )\,{\hat {e}}_{N}={\hat {e}}_{z}\times {\hat {e}}_{3}$ in Knotenrichtung weist, siehe Kreiseltheorie#Bezugssysteme und Euler-Winkel. Mit α = s/ρ ergibt sich die Geschwindigkeit ${\dot {\vec {T}}}={\dot {\vec {G}}}_{h}+[{\dot {G}}_{z}+s{\dot {\vartheta }}\sin(\vartheta )]\,{\hat {e}}_{z}+({\vec {G}}\cdot {\hat {e}}_{z}){\dot {\vartheta }}\,{\hat {e}}_{z}\times {\hat {e}}_{N}+\rho ({\dot {\varphi }}-\alpha {\dot {\psi }})\,{\hat {e}}_{z}\times {\hat {e}}_{3}$ Es existiert keine Horizontalgeschwindigkeit ${\dot {\vec {G}}}_{h}$ und keine Vertikalgeschwindigkeit ${\dot {G}}_{z}$ und der Neigungswinkel ϑ ist konstant. Bei still stehendem Aufstandspunkt T folgt aus dem letzten Summand ${\dot {\varphi }}=\alpha {\dot {\psi }}$ .

Herleitung der Funktion J_R(u)
Mit den Zwischenergebnissen aus der Herleitung der Präzessionsgeschwindigkeit und der Abkürzung u = cos(ϑ) entsteht der Drehimpuls ${\vec {L}}=L_{v}\,{\hat {e}}_{z}+L_{f}\,{\hat {e}}_{3}={\dot {\psi }}\{A\,{\hat {e}}_{z}+C[\alpha +(1-\gamma )u]\,{\hat {e}}_{3}\}$ und mit der Präzessionsgeschwindigkeit ${\dot {\psi }}={\sqrt {\frac {mgs}{C[\alpha +(1-\gamma )u]}}}={\frac {J_{\beta }}{\rho C{\sqrt {\alpha +(1-\gamma )u}}}}$ der Betrag des Jellett-Integrals $J_{R}(u):=\|{\vec {L}}\cdot {\vec {a}}\|={\vec {L}}\cdot (s{\hat {e}}_{3}+\rho {\hat {e}}_{z})=J_{\beta }{\frac {(\alpha +u)^{2}+\gamma (1-u^{2})}{\sqrt {\alpha +(1-\gamma )u}}}$ Darin ist J_β = ρ√(Cmgs) eine Kreisel eigene Konstante.

Wenn ❘J❘ = J_R(u) ist, ist die #Stabilität der stationären Bewegungen gegeben, weil dann die Gesamtenergie des Spielkreisels als Funktion des Neigungswinkels in u stationär ist[33]. Im Folgenden werden einige Merkmale von J_R(u) aufgeführt.

Die Randwerte

{\begin{aligned}J_{R1}:=&J_{R}(1)={\frac {J_{\beta }(1+\alpha )^{2}}{\sqrt {\alpha -\gamma +1}}}\\J_{R-1}:=&J_{R}(-1)={\frac {J_{\beta }(1-\alpha )^{2}}{\sqrt {\alpha +\gamma -1}}}\end{aligned}}

sind Kreisel eigene Konstanten. Wenn J_R(u) im Intervall u ∈ ⅅ ⊆ [-1:1] eine monotone Funktion von u ist, dann gibt es zu jedem Jellett-Integral zwischen den Randwerten in ⅅ genau eine mögliche Neigung des Kreisels, mit der der Kreisel regulär präzedieren kann. Wenn andernfalls irgendwo in ⅅ die Ableitung

{J_{R}}'(u):={\frac {\mathrm {d} J_{R}}{\mathrm {d} u}}=J_{\beta }{\frac {3[\alpha +(1-\gamma )u]^{2}-\gamma (1-\alpha ^{2}-\gamma )}{2[\alpha +(1-\gamma )u]^{\frac {3}{2}}}}

null ist, gibt es Extremwerte, in deren Umgebung zu einem Wert des Integrals zwei mögliche Neigungswinkel existieren. In physikalisch erreichbaren Nullstellen J_R'(u_m) = 0 gilt

{\begin{aligned}u_{m}=&{\frac {-\alpha +{\sqrt {{\frac {\gamma }{3}}(1-\alpha ^{2}-\gamma )}}}{1-\gamma }}\\J_{Rm}:=&J_{R}(u_{m})={\frac {4J_{\beta }}{1-\gamma }}\left({\frac {\gamma }{3}}(1-\alpha ^{2}-\gamma )\right)^{\frac {3}{4}}\end{aligned}}

was bei realen Bewegungen nur sein kann, wenn

½ < γ = A/C < 1 - α²

also beim abgeplatteten Kreisel, mit stumpfer Kreiselspitze α = s/ρ < 1/√2 ≈ 0,7.

Gesamtenergie des Spielkreisels

Die Gesamtenergie E = E_tra + E_rot + E_pot des Spielkreisels setzt sich zusammen aus seiner

Translationsenergie $E_{\text{tra}}={\tfrac {m}{2}}{\dot {\vec {G}}}\cdot {\dot {\vec {G}}}$ ,
Rotationsenergie bezüglich des Massenmittelpunkts $E_{\text{rot}}={\tfrac {1}{2}}{\vec {\omega }}\cdot {\vec {L}}={\tfrac {1}{2A}}{\vec {L}}\cdot {\vec {L}}+{\tfrac {A-C}{2AC}}L_{3}^{2}$ und
Lageenergie $E_{\text{pot}}=mg{\vec {G}}\cdot {\hat {e}}_{z}$

Mit den im Abschnitt #Bewegungsgleichungen angegebenen Zusammenhängen, insbesondere

{\vec {\omega }}={\frac {1}{A}}{\vec {L}}+{\frac {A-C}{AC}}({\vec {L}}\cdot {\hat {e}}_{3})\,{\hat {e}}_{3}

zeigt sich beim aufstehenden Kreisel:[17]

{\begin{aligned}E=&{\frac {J^{2}}{2|{\vec {a}}|^{2}\Theta _{a}}}+mg\rho (1+\alpha u)\\&+{\frac {1}{2}}{\vec {L}}_{\bot }\cdot \mathbf {\Theta } ^{-1}\cdot {\vec {L}}_{\bot }+{\frac {m}{2}}\left[{\dot {G}}_{h}^{2}+\left({\frac {s}{A}}{\vec {L}}_{\bot }\cdot ({\hat {e}}_{z}\times {\hat {e}}_{3})\right)^{2}\right]\end{aligned}}

Hier tauchen ein Drehimpuls ${\vec {L}}_{\bot }$ senkrecht zu ${\vec {a}}$ und #Jelletts Integral J auf, die dort definiert wurden. Die horizontale Schwerpunktsgeschwindigkeit ${\dot {G}}_{h}$ und der Drehimpuls ${\vec {L}}_{\bot }$ gehen bei Annäherung an eine stationäre Bewegung gegen null, sodass in einer solchen nur die ersten beiden Summanden übrig bleiben.[30]

Dissipation der Energie durch Reibung

Ohne Kontakt zur Unterlage bleibt die Gesamtenergie unter der hier getroffenen Beschränkung auf Gleitreibung erhalten. Bei Kontakt besitzt der unterste Kreiselpunkt keine Geschwindigkeit senkrecht zur Unterlage, also $({\dot {\vec {G}}}+{\vec {\omega }}\times {\vec {a}})\cdot {\hat {e}}_{z}=0$ . Damit und mit den #Bewegungsgleichungen berechnet sich die Zeitableitung der Gesamtenergie des aufstehenden Kreisels zu

{\dot {E}}=\left({\dot {\vec {G}}}+{\vec {\omega }}\times {\vec {a}}\right)\cdot {\vec {R}}

Die Reibkraft ${\vec {R}}$ ist der Geschwindigkeit des Aufstandspunkts in der Klammer stets entgegen gerichtet, weshalb das Skalarprodukt niemals positiv ist und die Gesamtenergie mit der Zeit monoton abnimmt.[20]

Bei einer stationären Bewegung auf der Unterlage muss der unterste Kreiselpunkt zu jedem Zeitpunkt ruhen, was bei der Rotation mit vertikaler Figurenachse und der #Reguläre Präzession mit still stehendem Massenmittelpunkt der Fall ist.

Stabilität der stationären Bewegungen

Eine stationäre Bewegung des Kreisels ist genau dann stabil, wenn seine Gesamtenergie in einem lokalen Minimum ist. Die Bedingungen hierfür fasst die Tabelle zusammen (u = cos(ϑ)).[34]

Symbol	Bewegungsform	Neigung	Stabilitätskriterium
▼	Rotation um lotrechte aufrechte Figurenachse	u = 1	γ < 1 + α und ❘J❘ > J_R1
▲	Rotation mit lotrecht hängender Figurenachse	u = -1	γ < 1 - α oder ❘J❘ < J_R-1
●	Reguläre Präzession	-1 < u < 1	γ > 1 - α² oder u > u_m

Unter den umgekehrten Bedingungen ist die Gesamtenergie in einem lokalen Maximum und die Bewegung instabil.

Symbol	Bewegungsform	Neigung	Kriterium für Instabilität
▽	Rotation um lotrechte aufrechte Figurenachse	u = 1	γ ≥ 1 + α oder ❘J❘ ≤ J_R1
△	Rotation mit lotrecht hängender Figurenachse	u = -1	γ ≥ 1 - α und ❘J❘ ≥ J_R-1
○	Reguläre Präzession	-1 < u < 1	γ ≤ 1 - α² und u ≤ u_m

Der Größenvergleich mit J_R1, J_R-1 oder u_m wird nur bei reellen Werten herangezogen.

Gesamtenergie der stationären Bewegungen
Die Gesamtenergie bleibt nicht nur beim abgehobenen Kreisel konstant, sondern auch dann, wenn der unterste Kreiselpunkt auf der Unterlage stillsteht, er also nicht gleitet. Dann rotiert der Kreisel mit lotrechter Figurenachse oder die untere Kreiselspitze rollt bei einer regulären Präzession gleitungslos auf der Unterlage ab. In diesen Gleichgewichtslösungen ruht der Massenmittelpunkt, ist ${\vec {L}}_{\bot }={\vec {0}}$ , die Energie in einem lokalen Extremum und mit gegebenen Jellett-Integral J eine Funktion des Neigungswinkels allein:[33] ${\begin{aligned}E=&{\frac {2J_{\beta }^{2}(1+\alpha u)[(\alpha +u)^{2}+\gamma (1-u^{2})]+\alpha J^{2}}{2\rho ^{2}C\alpha [(\alpha +u)^{2}+\gamma (1-u^{2})]}}\\E_{,u}:=&{\frac {\mathrm {d} E}{\mathrm {d} u}}={\frac {J_{\beta }^{2}[(\alpha +u)^{2}+\gamma (1-u^{2})]^{2}-J^{2}[\alpha +(1-\gamma )u]}{\rho ^{2}C[(\alpha +u)^{2}+\gamma (1-u^{2})]^{2}}}\\E_{,\vartheta }:=&{\frac {\mathrm {d} E}{\mathrm {d} \vartheta }}={\frac {\mathrm {d} E}{\mathrm {d} u}}{\frac {\mathrm {d} u}{\mathrm {d} \vartheta }}=-\sin(\vartheta )E_{,u}\end{aligned}}$ Die Konstante J_β = ρ√(Cmgs) hat die Dimension des Jellett-Integrals J. Die Gesamtenergie ist stationär, wenn E_,ϑ = 0 und somit sin(ϑ) = 0 ist, die Figurenachse also lotrecht, oder wenn E_,u = 0 ist. Der Zähler in E_,u kann mit der dritten binomischen Formel in ein Produkt umgewandelt werden, das verschwindet, wenn ❘J❘ = J_R(u), eine Identät die die #Reguläre Präzession erfüllt. Die Gesamtenergie ist bei Drehung mit lotrechter Figurenachse und bei der regulären Präzession stationär.

Minima der Energie
In einem Minimum der Gesamtenergie ist die Bewegung stabil und die zweite Ableitung der Gesamtenergie nach dem Neigungswinkel positiv. Es berechnet sich: ${\begin{aligned}E_{,uu}:=&{\frac {\mathrm {d} ^{2}E}{\mathrm {d} u^{2}}}={\frac {J^{2}}{\rho ^{2}C}}{\frac {3[\alpha +(1-\gamma )u]^{2}+\gamma (\alpha ^{2}+\gamma -1)}{[(\alpha +u)^{2}+\gamma (1-u^{2})]^{3}}}\\E_{,\vartheta \vartheta }:=&{\frac {\mathrm {d} ^{2}E}{\mathrm {d} \vartheta ^{2}}}=-\cos(\vartheta )E_{,u}+\sin ^{2}(\vartheta )E_{,uu}=-uE_{,u}+(1-u^{2})E_{,uu}\end{aligned}}$ Bei lotrechter Figurenachse (u = ±1) hat E_,ϑϑ das Vorzeichen von -u E_,u. Beim aufrecht stehenden Kreisel ist u = 1 und die Energie im Minimum, wenn E_,u < 0 also ${\begin{aligned}&(\alpha -\gamma +1)J^{2}>J_{\beta }^{2}(1+\alpha )^{4}\\\rightarrow \quad &\gamma <1+\alpha \quad {\text{und}}\quad \|J\|>{\frac {J_{\beta }(1+\alpha )^{2}}{\sqrt {\alpha -\gamma +1}}}=J_{R1}\end{aligned}}$ Beim lotrecht hängenden Kreisel ist u = -1 und die Energie im Minimum, wenn E_,u > 0 also ${\begin{aligned}&(\alpha +\gamma -1)J^{2}<J_{\beta }^{2}(1-\alpha )^{4}\\\rightarrow \quad &\gamma <1-\alpha \quad {\text{oder}}\quad \|J\|<{\frac {J_{\beta }(1-\alpha )^{2}}{\sqrt {\alpha +\gamma -1}}}=J_{R-1}\end{aligned}}$ Bei einer regulären Präzession ist die Figurenachse nicht lotrecht, -1 < u < 1, α + (1 - γ)u > 0 und E_,u = 0. Dann hat E_,ϑϑ das Vorzeichen von E_,uu, was wegen $E_{,uu}>0\quad \leftrightarrow \quad 3[\alpha +(1-\gamma )u]^{2}>\gamma (1-\alpha ^{2}-\gamma )$ unter den Bedingungen $\gamma >1-\alpha ^{2}\quad {\text{oder}}\quad u>{\frac {-\alpha +{\sqrt {{\frac {\gamma }{3}}(1-\alpha ^{2}-\gamma )}}}{1-\gamma }}=u_{m}$ positiv ist.

Einteilung des α-γ-Parameterraums
Die in Abb. 6 eingezeichneten Grenzen ergeben sich aus folgenden Bedingungen, die für reguläre Präzessionen relevant sind: ${\begin{aligned}\left.\alpha +(1-\gamma )u\right\|_{u=1}=0\;\rightarrow &\;\;\gamma =1+\alpha \\\left.\alpha +(1-\gamma )u\right\|_{u=-1}=0\;\rightarrow &\;\;\gamma =1-\alpha \\\left.\alpha +(1-\gamma )u\right\|_{u=u_{m}}=0\;\rightarrow &\;\;\gamma =1-\alpha ^{2}\\u_{m}=1\;\rightarrow &\;\;\gamma _{1,2}={\frac {1}{8}}(1+\alpha )\left(7-\alpha \pm {\sqrt {(7-\alpha )^{2}-48}}\right)\\u_{m}=-1\;\rightarrow &\;\;\gamma ={\frac {1}{8}}(1-\alpha )\left(7+\alpha +{\sqrt {(7+\alpha )^{2}-48}}\right)\\J_{R-1}=J_{R1}\;\rightarrow &\;\;\gamma ={\frac {(1-\alpha ^{2})(1+3\alpha ^{2})}{1+6\alpha ^{2}+\alpha ^{4}}}\end{aligned}}$ Die ersten drei Bedingungen beranden Gebiete, in denen die Präzessionsgeschwindigkeit über alle Grenzen wachsen kann und reguläre Präzessionen nicht mit jeder Neigung möglich sind (Ib, IIb). Die beiden folgenden Bedingungen beranden Gebiete, in denen J_R(u) im physikalisch erreichbaren Bereich ein lokales Minimum J_Rm = J_R(u_m) aufweist, der Kreisel also zu einem gegebenen ❘J❘ ∈ [ J_Rm: min(J_R-1, J_R1)] reguläre Präzessionen mit zwei verschiedenen Neigungswinkeln ausführen kann. 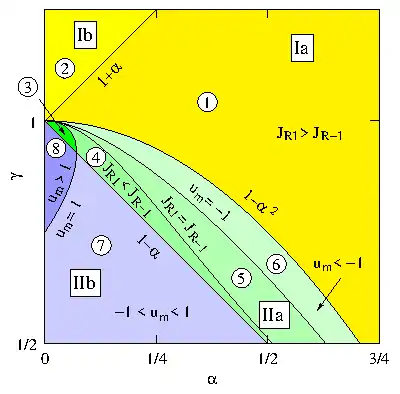Die sechste und letzte Bedingung trennt die Bereiche ④ und ⑤, in denen es an einer Stelle u_k ∈ ]-1: 1[ eine reguläre Präzession mit ❘J❘ = J_R-1 oder ❘J❘ = J_R1 gibt: Im Bereich ④ ist J_R-1 > J_R1, J_R(u) im Intervall [-1: u_k[ monoton fallend und gibt es zu jedem ❘J❘ ∈ ]J_Rm: J_R1] zwei reguläre Präzessionen mit u_1,2 ∈ [u_k: 1]. Im Bereich ⑤ ist andererseits J_R-1 < J_R1, gibt es zu jedem ❘J❘ ∈ ]J_Rm: J_R-1] zwei reguläre Präzessionen mit u_1,2 ∈ [-1: u_k] und ist J_R(u) im Intervall ]u_k: 1] monoton steigend.

Abb. 6: α-γ-Parameterraum des Spielkreisels

Die Spielkreisel lassen sich durch ihre Parameter α = s/ρ und γ = A/C acht Bereichen zuordnen, in denen sie gleiches Stabilitätsverhalten aufweisen, siehe Abb. 6. Die acht Bereiche lassen sich wiederum in vier Fälle Ia/b, IIa/b gruppieren.[35]

Kreiseltyp I: 1 - α² ≤ γ

Die Funktion J_R(u) für die #Reguläre Präzession ist, wo sie im physikalisch erreichbaren Bereich reell ist, monoton und es gibt zu jedem J höchstens eine reguläre Präzession, die dann auch stabil ist (●).

Die Drehung um die hängende lotrechte Figurenachse mit u = -1 ist stabil, wenn ❘J❘ < J_R-1 (▲) und instabil, wenn ❘J❘ ≥ J_R-1 (△).

Kreiseltyp Ia: 1 - α² ≤ γ < 1 + α

Reguläre Präzessionen sind im gesamten Intervall -1 < u < 1 möglich und stabil (●).

Rotationen um die vertikale aufrechte Figurenachse mit u = 1 ist stabil, wenn ❘J❘ > J_R1 (▼) und instabil, wenn ❘J❘ ≤ J_R1 (▽).

Kreiseltyp Ib: 1 + α ≤ γ

Reguläre Präzessionen sind nur im Intervall -1 < u < ${\tfrac {\alpha }{\gamma -1}}$ möglich und dann auch stabil (●).

Die Drehung um die vertikale aufrechte Figurenachse mit u = 1 ist instabil (▽).

Kreiseltyp II: γ ≤ 1 - α²

Wegen γ > ½ ist bei diesen Kreiseln α < 1/√2 ≈ 0,7.

In den Zonen ③, ⑥ und ⑧ ist die Funktion J_R(u), wo sie im physikalisch erreichbaren Bereich reell ist, monoton, wohingegen in den anderen Gebieten, ④, ⑤ und ⑦, ein lokales Minimum J_Rm = J_R(u_m) auftritt.

Die Rotation mit lotrecht stehender Figurenachse (u = 1) ist stabil, wenn ❘J❘ > J_R1 (▼), und sonst instabil (▽).

Kreiseltyp IIa: 1 - α < γ ≤ 1 - α²

Der Kreisel kann mit jeder Neigung u ∈ [-1: 1] eine reguläre Präzession ausführen, denn die Funktion J_R(u) ist im ganzen Intervall definiert.

In ③ ist u_m > 1 > u und die zugehörige reguläre Präzession instabil (○).
In ④ und ⑤ gibt es ein Minimum J_Rm bei u_m ∈ [-1: 1]. Die regulären Präzessionen mit u < u_m sind instabil (○) und die anderen stabil (●). Zu jedem ❘J❘ ∈ ] J_Rm: min(J_R-1, J_R1)] gibt es zwei reguläre Präzessionen mit unterschiedlicher Neigung, wobei die schwächer geneigte dementsprechend stabil (●) und die stärker geneigte instabil ist (○).
In ⑥ ist u_m < -1 < u und die zugehörige reguläre Präzession stabil (●).

Die Rotation mit lotrecht hängender Figurenachse (u = -1) ist stabil, wenn ❘J❘ < J_R-1 (▲), und sonst instabil (△).

Kreiseltyp IIb: ½ < γ ≤ 1 - α

Reguläre Präzessionen können nur im Intervall $-{\tfrac {\alpha }{1-\gamma }}<u<1$ und mit betraglich beliebig großem J auftreten. Im Gebiet ⑧ ist u_m > 1 und es gibt zu jedem ❘J❘ > J_R1 genau eine reguläre Präzession und die ist instabil (○). In der Zone ⑦ fällt J_R(u) aus dem Unendlichen kommend auf das Minimum J_Rm ab um anschließend nach J_R1 anzusteigen. Im abfallenden Ast ]∞: J_R1] gibt es zu jedem J eine reguläre Präzession und die ist instabil (○). Zwischen J_Rm und J_R1 gibt es zu jedem J zwei reguläre Präzessionen, von denen die weniger geneigte stabil (●) und die andere instabil ist (○).

Der lotrecht hängende Kreisel ist stabil (▲).

Weblinks

Wiktionary: Spielkreisel – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen

Commons: Spielkreisel – Sammlung von Bildern, Videos und Audiodateien

Einzelnachweise

Magnus (1971), S. 266, Grammel (1920), S. 111 und 123, siehe Literatur.
Rauch-Wojciechowski, Sköldstam und Glad (2005), S. 352.
Magnus (1971), S. 266.
Grammel (1920), S. 111.
Felix Klein, Conr. Müller: Encyklopädie der Mathematischen Wissenschaften mit Einschluss ihrer Anwendungen. Mechanik. Hrsg.: Akademien der Wissenschaften zu Göttingen, Leipzig, München und Wien. Vierter Band, 1. Teilband. B. G. Teubner, 1908, ISBN 978-3-663-16021-2, S. 546, doi:10.1007/978-3-663-16021-2 (eingeschränkte Vorschau in der Google-Buchsuche [abgerufen am 24. Januar 2020] siehe auch wikisource}).
Clifford Truesdell: Die Entwicklung des Drallsatzes. In: Gesellschaft für Angewandte Mathematik und Mechanik (Hrsg.): Zeitschrift für Angewandte Mathematik und Mechanik (= Heft 4/5). Band 44, April 1964, S. 154, doi:10.1002/zamm.19640440402 (wiley.com).
Joseph-Louis Lagrange: Mécanique Analytique. Tome Second. Corucier, Paris 1815, S. 265 f. (französisch, archive.org [abgerufen am 20. August 2017]). oder Joseph-Louis Lagrange: Analytische Mechanik. Vandenhoeck und Ruprecht, Göttingen 1797 (archive.org [abgerufen am 20. August 2017] Deutsche Übersetzung von Friedrich Murhard).
Magnus (1971), S. 266.
J. H. Jellett: A treatise on the theory of friction. Macmillan Publishers, London 1872, S. 185 (archive.org [abgerufen am 15. Dezember 2018]). In der Kreiseltheorie werden Konstanten der Bewegung als Integral bezeichnet, weil ihre Zeitableitung verschwindet und somit umgekehrt das Zeitintegral eine Konstante liefert.
siehe Rauch-Wojciechowski, Sköldstam und Glad (2005), S. 333 und die Literaturangaben dort.
siehe Rauch-Wojciechowski, Sköldstam und Glad (2005)
Edward Routh: A TREATISE ON THE STABILITY OF A GIVEN STATE OF MOTION. PARTICULARLY STEADY MOTION. Macmillan Publishers, London 1877 (archive.org – Dieses Essay wurde 1877 an der Cambridge University mit dem Adams-Preis ausgezeichnet.).
Magnus (1971), S. 271+273, Kuypers und Ucke (1994), S. 215.
Rauch-Wojciechowski, Sköldstam und Glad (2005), S. 361.
Kuypers und Ucke (1994), S. 215.
Grammel (1920), S. 113.
Rauch-Wojciechowski, Sköldstam und Glad (2005), S. 339.
Grammel (1920), S. 116.
Magnus (1971), S. 267, Rauch-Wojciechowski, Sköldstam und Glad (2005), S. 336 oder Ciocci und Langerock (2007).
Rauch-Wojciechowski, Sköldstam und Glad (2005), S. 337.
Kuypers und Ucke (1994), S. 214.
Grammel (1920), S. 124 ff.
Grammel (1920), S. 125 f.
Grammel (1920), S. 127.
M. C. Ciocci, B. Langerock: Dynamics of the Tippe Top via Routhian Reduction. In: Regular and Chaotic Dynamics. Band 12, Nr. 6. Springer Nature, 2007, ISSN 1468-4845, S. 602–614, doi:10.1134/S1560354707060032, arxiv:0704.1221 (englisch, Die Euler-Winkel φ und ψ haben vertauschte Bedeutungen.).
Rauch-Wojciechowski, Sköldstam und Glad (2005), S. 336.
Rauch-Wojciechowski, Sköldstam und Glad (2005), S. 335.
Rauch-Wojciechowski, Sköldstam und Glad (2005), S. 338.
Edward Routh: Die Dynamik der Systeme starrer Körper. Die Höhere Dynamik. zweiter Band. B. G. Teubner, Leipzig 1898, S. 192 (archive.org).
Rauch-Wojciechowski, Sköldstam und Glad (2005), S. 340.
Rauch-Wojciechowski, Sköldstam und Glad (2005), S. 343.
Rauch-Wojciechowski, Sköldstam und Glad (2005), S. 347.
Rauch-Wojciechowski, Sköldstam und Glad (2005), S. 353 ff. Dort ist cos(ϑ) = -u.
Rauch-Wojciechowski, Sköldstam und Glad (2005), S. 356. Dort ist η₃=-u, λ=J und β=J_β. Die Formelzeichen sind im Abschnitt #Reguläre Präzession definiert.
Rauch-Wojciechowski, Sköldstam und Glad (2005), S. 358 ff. Dort ist η₃=-u, λ=J und β=J_β.

Literatur

K. Magnus: Kreisel: Theorie und Anwendungen. Springer, 1971, ISBN 978-3-642-52163-8, S. 266 ff. (eingeschränkte Vorschau in der Google-Buchsuche [abgerufen am 20. Februar 2018]).
R. Grammel: Der Kreisel. Seine Theorie und seine Anwendungen. Vieweg Verlag, Braunschweig 1920, DNB 451641280, S. 111 ff. und 123 ff. (archive.org – "Schwung" bedeutet Drehimpuls, „Drehstoß“ etwa Drehmoment und „Drehwucht“ Rotationsenergie, siehe S. VII).
R. Grammel: Der Kreisel. Seine Theorie und seine Anwendungen. 2. überarb. Auflage. Band 1. Springer, Berlin, Göttingen, Heidelberg 1950, S. 51, 69, 79.
S. Rauch-Wojciechowski, M. Sköldstam, T. Glad: Mathematical analysis of the tippe top. In: Regular and Chaotic Dynamics. Band 10, Nr. 4. Springer Nature, 2005, ISSN 1468-4845, S. 333–362, doi:10.1070/RD2005v010n04ABEH000319 (turpion.org [abgerufen am 15. Dezember 2018]).
Friedhelm Kuypers, Christian Ucke: Steh' auf Kreisel! In: Physik in unserer Zeit. Band 25, Nr. 5. Wiley Online Library, 1994, ISSN 0031-9252, S. 214–215, doi:10.1002/piuz.19940250503 (wiley.com [abgerufen am 22. Februar 2019]).

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Magnus (1971), S. 266, Grammel (1920), S. 111 und 123, siehe Literatur.

[rauch352-2] Rauch-Wojciechowski, Sköldstam und Glad (2005), S. 352.

[3] Magnus (1971), S. 266.

[grammel111-4] Grammel (1920), S. 111.

[5] Felix Klein, Conr. Müller: Encyklopädie der Mathematischen Wissenschaften mit Einschluss ihrer Anwendungen. Mechanik. Hrsg.: Akademien der Wissenschaften zu Göttingen, Leipzig, München und Wien. Vierter Band, 1. Teilband. B. G. Teubner, 1908, ISBN 978-3-663-16021-2, S. 546, doi:10.1007/978-3-663-16021-2 (eingeschränkte Vorschau in der Google-Buchsuche [abgerufen am 24. Januar 2020] siehe auch wikisource}).

[6] Clifford Truesdell: Die Entwicklung des Drallsatzes. In: Gesellschaft für Angewandte Mathematik und Mechanik (Hrsg.): Zeitschrift für Angewandte Mathematik und Mechanik (= Heft 4/5). Band 44, April 1964, S. 154, doi:10.1002/zamm.19640440402 (wiley.com).

[7] Joseph-Louis Lagrange: Mécanique Analytique. Tome Second. Corucier, Paris 1815, S. 265 f. (französisch, archive.org [abgerufen am 20. August 2017]). oder Joseph-Louis Lagrange: Analytische Mechanik. Vandenhoeck und Ruprecht, Göttingen 1797 (archive.org [abgerufen am 20. August 2017] Deutsche Übersetzung von Friedrich Murhard).

[magnus266-8] Magnus (1971), S. 266.

[jellett-9] J. H. Jellett: A treatise on the theory of friction. Macmillan Publishers, London 1872, S. 185 (archive.org [abgerufen am 15. Dezember 2018]). In der Kreiseltheorie werden Konstanten der Bewegung als Integral bezeichnet, weil ihre Zeitableitung verschwindet und somit umgekehrt das Zeitintegral eine Konstante liefert.

[10] siehe Rauch-Wojciechowski, Sköldstam und Glad (2005), S. 333 und die Literaturangaben dort.

[Rauch-11] siehe Rauch-Wojciechowski, Sköldstam und Glad (2005)

[12] Edward Routh: A TREATISE ON THE STABILITY OF A GIVEN STATE OF MOTION. PARTICULARLY STEADY MOTION. Macmillan Publishers, London 1877 (archive.org – Dieses Essay wurde 1877 an der Cambridge University mit dem Adams-Preis ausgezeichnet.).

[13] Magnus (1971), S. 271+273, Kuypers und Ucke (1994), S. 215.

[14] Rauch-Wojciechowski, Sköldstam und Glad (2005), S. 361.

[15] Kuypers und Ucke (1994), S. 215.

[grammel113-16] Grammel (1920), S. 113.

[rauch339-17] Rauch-Wojciechowski, Sköldstam und Glad (2005), S. 339.

[grammel116-18] Grammel (1920), S. 116.

[19] Magnus (1971), S. 267, Rauch-Wojciechowski, Sköldstam und Glad (2005), S. 336 oder Ciocci und Langerock (2007).

[rauch337-20] Rauch-Wojciechowski, Sköldstam und Glad (2005), S. 337.

[21] Kuypers und Ucke (1994), S. 214.

[22] Grammel (1920), S. 124 ff.

[23] Grammel (1920), S. 125 f.

[24] Grammel (1920), S. 127.

[Ciocci&Langerock-25] M. C. Ciocci, B. Langerock: Dynamics of the Tippe Top via Routhian Reduction. In: Regular and Chaotic Dynamics. Band 12, Nr. 6. Springer Nature, 2007, ISSN 1468-4845, S. 602–614, doi:10.1134/S1560354707060032, arxiv:0704.1221 (englisch, Die Euler-Winkel φ und ψ haben vertauschte Bedeutungen.).

[26] Rauch-Wojciechowski, Sköldstam und Glad (2005), S. 336.

[27] Rauch-Wojciechowski, Sköldstam und Glad (2005), S. 335.

[28] Rauch-Wojciechowski, Sköldstam und Glad (2005), S. 338.

[29] Edward Routh: Die Dynamik der Systeme starrer Körper. Die Höhere Dynamik. zweiter Band. B. G. Teubner, Leipzig 1898, S. 192 (archive.org).

[rauch340-30] Rauch-Wojciechowski, Sköldstam und Glad (2005), S. 340.

[31] Rauch-Wojciechowski, Sköldstam und Glad (2005), S. 343.

[32] Rauch-Wojciechowski, Sköldstam und Glad (2005), S. 347.

[rauch353-33] Rauch-Wojciechowski, Sköldstam und Glad (2005), S. 353 ff. Dort ist cos(ϑ) = -u.

[34] Rauch-Wojciechowski, Sköldstam und Glad (2005), S. 356. Dort ist η₃=-u, λ=J und β=J_β. Die Formelzeichen sind im Abschnitt #Reguläre Präzession definiert.

[35] Rauch-Wojciechowski, Sköldstam und Glad (2005), S. 358 ff. Dort ist η₃=-u, λ=J und β=J_β.