Pseudoreguläre Präzession

Die pseudoreguläre Präzession ist in der Kreiseltheorie eine Kreiselbewegung, die augenscheinlich der regulären Präzession symmetrischer Kreisel gleicht, bei der bei genauer Betrachtung jedoch kleine, mit dem bloßen Auge kaum wahrnehmbare, schnelle, überlagernde Oszillationen um den Präzessionskegel stattfinden[1]. Der Drehimpuls ist nahe an der Hauptachse mit dem größten oder dem kleinsten Hauptträgheitsmoment orientiert, und der Kreisel dreht um diese Hauptachse so schnell, dass alle seine anderen Drehungen, die er außerdem noch ausführt, damit verglichen langsam sind.[2]

Die pseudoreguläre Präzession ist ein wichtiger Punkt der Kreiseltheorie und hat ob der Häufigkeit ihres Auftretens und ihrer paradoxen Eigenschaften größtes Interesse seitens der Naturphilosophie auf sich gezogen. Die pseudoreguläre Präzession stellt sich bei allgemeineren Umständen ein als die reguläre Präzession.[3] Die erfolgenden Erzitterungen der Drehachse werden nach einem der Astronomie entlehnten Wort Nutationen genannt[4].

Der Begriff wurde von Felix Klein und Arnold Sommerfeld 1898 geprägt.[5]

Paradoxie der pseudoregulären Präzession

Bei einem Peitschenkreisel oder Wurfkreisel, der durch Abzug einer Schnur in rasche Drehung versetzt und dann auf einer waagerechten Unterlage im Schwerefeld der Erde sich selbst überlassen wird, umläuft die Figurenachse mit gleichförmiger Geschwindigkeit wie bei einer regulären Präzession einen Kreiskegel um die Senkrechte. Diese Tatsache ist doppelt erstaunlich, weil

allen Erwartungen zum Trotz die Punkte auf der Figurenachse unter Einwirkung der lotrecht wirkenden Schwerkraft eine Kreisbahn in dazu senkrechter, horizontaler Ebene verfolgen und
die reguläre Präzession theoretisch nur unter speziellen Umständen auftritt, sie sich jedoch im Experiment anscheinend bei beliebiger Wahl der Ausgangsbedingungen einstellt.

Während ersteres eine natürliche Folge des Zusammenspiels von Schweremoment und Drehimpuls ist, ist gegen letztere Auffassung zunächst einzuwenden, dass das Beobachtungsergebnis nicht genau ist. Denn die Kreiselbewegung hat nur eine äußerliche Ähnlichkeit mit der regulären Präzession, weil die eingangs erwähnten kleinen Oszillationen unbeachtet bleiben. In Abgrenzung zur regulären Präzession wird der beobachtete Ablauf daher pseudoregulär genannt. Die Illusion der Ähnlichkeit mit der regulären Präzession wird dadurch noch verstärkt, dass die pseudoreguläre Präzession durch sekundäre Effekte wie Reibung und elastische Verformung tatsächlich rasch in eine reguläre Präzession übergeht. Zudem sind die beim Peitschen- oder Wurfkreisel eingestellten Anfangsbedingungen keineswegs beliebig, sondern im Gegenteil ziemlich speziell: Der kraftvolle Abzug der Kordel versieht den Kreisel immer mit einem beträchtlichen Drehimpuls, der nahe der Figurenachse ausgerichtet ist. Die Häufigkeit ihres Vorkommens verdankt die pseudoreguläre Präzession somit einem Auswahl- oder Designeffekt.

Symmetrische Kreisel

Lagrange-Kreisel

Bei der pseudoregulären Präzession des symmetrischen Lagrange-Kreisels ist der Drehimpuls groß und in der Nähe der Figurenachse ausgerichtet. Nähe bedeutet hier genauer, dass die Oszillationen des Locus der Figurenachse auf der Einheitskugel mit dem bloßen Auge nicht wahrnehmbar sind. Der Drehimpuls L hat eine hinreichende Größe, wenn L² > 100CGs, worin C das axiale Hauptträgheitsmoment, G die Gewichtskraft und s der Abstand des Massenmittelpunkts vom Stützpunkt ist. Weil der Drehimpuls nach Voraussetzung vom Eigendrehimpuls L₃ dominiert wird, kann statt des Betrages L des Drehimpulses auch der Eigendrehimpuls L₃ zur Qualifizierung benutzt werden.[6]

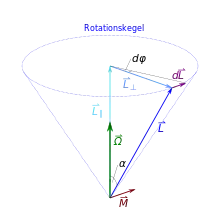
Rotationskegel des Drehimpulses, der bei der pseudoregulären Präzession nahe der Figurenachse liegt

Die pseudoreguläre Präzession kann sinnfällig vereinfacht dargestellt werden, siehe Bild. Denn weil das Moment der Gewichtskraft immer senkrecht auf der Figurenachse steht, die in der Nähe des Drehimpulses angenommen wird, ist nach dem Drallsatz ${\vec {M}}={\dot {\vec {L}}}$ die Änderungsgeschwindigkeit des Drehimpulses etwa senkrecht zu ihm. Daher bewegt sich der Drehimpuls in guter Näherung auf einem Kegel, dem Präzessionskegel, um die senkrechte Präzessionsachse mit einer Präzessions-Kreisfrequenz ${\vec {\Omega }}$ gemäß

{\vec {M}}={\dot {\vec {L}}}={\vec {\Omega }}\times {\vec {L}}

Das ist analog zu ${\vec {v}}={\vec {\omega }}\times {\vec {r}}$ , wo sich die Geschwindigkeit ${\vec {v}}$ bei einer reinen Rotation mit Winkelgeschwindigkeit ${\vec {\omega }}$ aus dem Abstand ${\vec {r}}$ zu einem Fixpunkt auf der Drehachse ergibt. In Komponenten mit ${\vec {M}}=Gs\sin(\alpha ){\hat {e}}_{N},\;{\vec {\Omega }}=\Omega {\hat {e}}_{z},\;{\vec {L}}\approx C\omega _{3}{\hat {e}}_{3}$ und ${\hat {e}}_{z}\times {\hat {e}}_{3}=\sin(\alpha ){\hat {e}}_{N}$ schreibt sich das

M=Gs\sin(\alpha )=\Omega C\omega _{3}\sin(\alpha )\quad \rightarrow \quad \Omega ={\frac {Gs}{C\omega _{3}}}

Darin sind ê_{N, z, 3} die Richtungsvektoren der Knotenlinie ê_z × ê₃, der Lotlinie bzw. der Figurenachse. Die Präzessionsfrequenz Ω wächst also mit dem Moment und ist umso kleiner je größer der Eigendrehimpuls L₃ = Cω₃ um die Figuren- oder 3-Achse ist. Die Präzessionsfrequenz entspricht derjenigen bei der regulären Präzession des schnellen Kreisels, in die der Kreisel durch sekundäre Effekte wie Reibung und elastische Verformung rasch übergeht. Weil sich die Figurenachse nur in der Nähe des Drehimpulsvektors befindet, umläuft sie diesen rasch auf engem Kegel.

Der Umlauf des Locus der Figurenachse um den Drehimpulsvektor kann durch eine Zykloide in einer Tangentialebene an die Einheitskugel angenähert werden:[7]

\xi =r\omega t+\rho \sin(\omega t),\;\eta =r+\rho \cos(\omega t)

mit

r={\frac {AGs\sin(\vartheta _{0})}{L_{3}^{2}}},\;\rho ={\frac {L_{z}-L_{3}\cos(\vartheta _{0})}{L_{3}\sin(\vartheta _{0})}}-r,\;\omega ={\frac {L_{3}}{A}}

Darin ist ξ die Koordinate parallel zum Breitenkreis, auf dem der Drehimpuls näherungsweise umläuft, r der Radius des Gangkreises, ω die Umlaufgeschwindigkeit der Figurenachse um den Drehimpuls auf dem Gangkreis und η die Auslenkung senkrecht zum Breitenkreis[8]. Der Index 0 markiert den mittleren Wert des Neigungswinkels.

Der Cosinus u = cos(ϑ) des Neigungswinkels ϑ und der Präzessionswinkel ψ sind näherungsweise

u=u_{0}+{\hat {u}}\sin(\omega t),\;\psi ={\frac {Gs}{L_{3}}}t+{\frac {\hat {u}}{1-u_{0}^{2}}}\cos(\omega t)

Darin ist

{\hat {u}}={\frac {L_{z}-L_{3}u_{0}}{L_{3}}}-{\frac {AGs}{L_{3}^{2}}}(1-u_{0}^{2}),\;\omega ={\frac {L_{3}}{A}}

Der Spielkreisel vermag bei gleicher Bauform und gleichen Anfangsbedingungen eine gleichschnelle pseudoreguläre Präzession auszuführen, allerdings vollziehen bei ihm sowohl der Massenmittelpunkt als auch der Aufstandspunkt feine Schwankungen, weswegen von einem Nutationskegel nicht mehr die Rede sein kann

Gorjatschew-Tschaplygin-Kreisel

Wenn beim Gorjatschew-Tschaplygin-Kreisel die Winkelgeschwindigkeit um die Schwerpunktsachse vom Stützpunkt zum Schwerpunkt sehr groß ist, dann bewegt sich der Kreisel analog zur pseudoregulären Präzession des Lagrange-Kreisels.[9]

Unsymmetrische Kreisel

Der allgemeine unsymmetrische Kreisel kann eine gleichförmige Drehung nur in Form der Staude-Drehung ausführen, denn die Griolische Präzession ist nur bei spezieller Massenverteilung möglich. Eine pseudoreguläre Präzession kann der unsymmetrische Kreisel dann ausführen, wenn er sich so rasch um eine Hauptträgheitsachse e dreht, dass alle anderen von ihm ausgeführten Drehungen verglichen damit langsam sind. Die sich ergebende Präzession gleicht der eines symmetrischen Kreisels und erfolgt auch mit derselben Präzessionsgeschwindigkeit. Stabil ist diese Bewegung jedoch nur dann, wenn – wie beim Euler-Kreisel – besagte Hauptträgheitsachse e das größte oder das kleinste Hauptträgheitsmoment besitzt.[10]

Um diese Präzession vollführt die Drehachse des Kreisels näherungsweise Epizykeln, wie sie bis ins 17. Jahrhundert hinein für die Erklärung der Planetenbahnen benutzt wurden. Dabei rollen vier sphärische Kreise mit je gleichförmiger Winkelgeschwindigkeit aufeinander ab, wobei der erste Kreis auf einem waagerechten Breitenkreis bleibt und die Drehachse auf dem vierten liegt.

Wenn die schnelle Eigendrehung p um die 1-Achse mit dem Hauptträgheitsmoment A erfolgt, dann rollt der erste Kreis mit derselben Geschwindigkeit

\Omega ={\frac {Gs_{1}}{Ap}}

mit der der #Lagrange-Kreisel pseudoregulär präzessiert, worin G die Gewichtskraft und s₁ der Abstand des Massenmittelpunkts vom Stützpunkt entlang der 1-Achse ist.

„Zwei der vier Nutationen des schnellen unsymmetrischen Kreisels, nämlich die beiden mit den Umlaufsgeschwindigkeiten p + σ und p - σ sind von den Anfangsbedingungen abhängig, das Verhältnis b/c ihrer sphärischen Weiten allerdings nur von den Hauptdrehmassen. Die beiden anderen Nutationen sind von außen nicht zu beeinflussen; und zwar erfolgt die eine von ihnen mit der Eigendrehgeschwindigkeit des Kreisels, herrührend von der abseitigen Lage (s₂,s₃) des Schwerpunkts, und sie verschwindet, wenn der Schwerpunkt entweder auf der Drehachse liegt, oder wenn diese waagerecht präzessiert; die andere erfolgt mit der doppelten Eigendrehgeschwindigkeit des Kreisels, rührt von der Verschiedenheit der Drehmassen B und C der beiden anderen Hauptachsen her und verschwindet, wenn entweder diese beiden Drehmassen einander gleich sind oder der Schwerpunkt in der zur Drehachse normalen Stützpunktsebene liegt, und sie ist am größten, wenn die Drehachse waagerecht präzessiert.“

– Richard Grammel: Der Kreisel, Seine Theorie und seine Anwendungen (1950) S. 211.

Die erwähnten Größen lauten

\sigma =p{\sqrt {\frac {(A-B)(A-C)}{BC}}},\;{\frac {b}{c}}={\sqrt {{\frac {C}{B}}{\frac {C-A}{B-A}}}}

Die Parameter b und c sind als klein angenommen und bleiben in diesem Rahmen unbestimmt, solange ihr Verhältnis den geforderten Wert besitzt. Die Radikanden sind positiv, wenn A das größte oder kleinste der Hauptträgheitsmomente oder Drehmassen ist.

Weblinks

Commons: Kreisel – Sammlung von Bildern, Videos und Audiodateien

Einzelnachweise

Grammel (1950), S. 75ff.
Grammel (1950), S. 205.
Klein und Sommerfeld (2010), S. 291.
Grammel (1950), S. 76.
Klein und Sommerfeld (2010), S. 209 und 291.
Klein und Sommerfeld (2010), S. 291 f.
Klein und Sommerfeld (2010), S. 297.
Grammel (1950), S. 77.
Leimanis (1965), S. 92.
Grammel (1950), S. 204 ff.

Literatur

K. Magnus: Kreisel: Theorie und Anwendungen. Springer, 1971, ISBN 978-3-642-52163-8, S. 20 (eingeschränkte Vorschau in der Google-Buchsuche [abgerufen am 20. Februar 2018]).
R. Grammel: Der Kreisel. Theorie des Kreisels. 2. überarb. Auflage. Band 1. Springer, Berlin, Göttingen, Heidelberg 1950, DNB 451641299, S. 75 ff., 204 ff. oder
R. Grammel: Der Kreisel. Seine Theorie und seine Anwendungen. Vieweg Verlag, Braunschweig 1920, DNB 451641280, S. 61 ff., 134 ff. (archive.org – „Schwung“ bedeutet Drehimpuls, „Drehstoß“ Drehmoment und „Drehwucht“ Rotationsenergie).
F. Klein, A. Sommerfeld: The Theory of the Top. Development of the Theory in the Case of the Heavy Symmetric Top. Vol. II. Springer, New York 2010, ISBN 978-0-8176-4824-4, S. 291, doi:10.1007/978-0-8176-4827-5 (Übersetzung des Originals von 1897, s. S. IX.).
Eugene Leimanis: The General Problem of the Motion of Coupled Rigid Bodies about a Fixed Point. Springer Verlag, Berlin, Heidelberg 1965, ISBN 978-3-642-88414-6, S. 92, doi:10.1007/978-3-642-88412-2 (englisch, eingeschränkte Vorschau in der Google-Buchsuche [abgerufen am 21. März 2018]).

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Grammel (1950), S. 75ff.

[2] Grammel (1950), S. 205.

[3] Klein und Sommerfeld (2010), S. 291.

[4] Grammel (1950), S. 76.

[5] Klein und Sommerfeld (2010), S. 209 und 291.

[6] Klein und Sommerfeld (2010), S. 291 f.

[7] Klein und Sommerfeld (2010), S. 297.

[8] Grammel (1950), S. 77.

[9] Leimanis (1965), S. 92.

[10] Grammel (1950), S. 204 ff.