Schwingfestigkeit

Die Schwingfestigkeit (engl. fatigue behaviour) ist ein Begriff aus der Werkstoffkunde und bezeichnet das Verformungs- und Versagensverhalten von Werkstoffen bei zyklischer Beanspruchung. Untersucht wird sie im Wöhlerversuch, aus dessen Ergebnissen die Wöhlerkurve konstruiert werden kann. Die Wöhlerkurve gibt in Abhängigkeit von der Ausschlagsspannung die Anzahl der ertragbaren Lastwechsel bis zum erwarteten Schwingbruch an. Außerdem kann die Wöhlerkurve in die Bereiche Kurzzeitfestigkeit, Zeitfestigkeit oder Dauerfestigkeit unterteilt werden. Für die Darstellung der Dauerfestigkeit können Diagramme wie das Haigh-Diagramm oder das Smith-Diagramm verwendet werden. Zeitfestigkeit bzw. Betriebsfestigkeit sowie Dauerfestigkeit haben einen großen Einfluss auf die Dimensionierung von Bauteilen in den Ingenieurwissenschaften.

Abgrenzung der schwingenden von der statischen Beanspruchung

Die Belastung eines Bauteils oder einer Werkstoffprobe kann statisch oder dynamisch erfolgen. Bei einer statischen Beanspruchung können Werkstoffkennwerte wie die Streckgrenze oder die Zugfestigkeit in einem Zugversuch bestimmt werden. Statische Belastung meint hier die Belastung eines Körpers (Gegenstandes) mit einer konstanten Kraft aus einer konstanten Richtung. Als Beispiel sei hier das Abstellen eines Steines auf einem Tisch erwähnt. Der Stein hat eine konstante Masse und übt durch die Erdbeschleunigung eine konstante Kraft auf den Tisch aus. Übersteigt die Kraft einen bestimmten Wert, so wird der Tisch zusammenbrechen.

Bei dynamischer Beanspruchung dagegen wird das Bauteil Lastwechseln unterzogen, dabei sinkt die zulässige Spannung in einem Werkstoff: Ein Bruch kann eintreten, auch wenn die Zugfestigkeit noch nicht erreicht wurde und oft, ohne dass der linear-elastische Bereich des Spannungs-Dehnungs-Diagramms verlassen wurde. Eine Schraube, die z. B. zur Befestigung eines Auspuffs am Fahrzeug dient, kann wegen der schwingenden Belastung der Fahrzeugbewegung brechen, obwohl die eigentliche Dehngrenze nicht erreicht wurde. Dieser Effekt kann durch Korrosion und/oder Temperaturänderungen noch verstärkt werden. Mit dem Aufkommen der Eisenbahn entstanden erstmals derartige Probleme. Laut statischen Berechnungen hätten Räder der Wagen die Beanspruchungen bei der Fahrt ohne Weiteres aufnehmen müssen, ohne dabei Schaden zu nehmen. Vermehrt fielen jedoch Eisenbahnwagen aus, weil die Radsatzwellen gebrochen waren. August Wöhler untersuchte dieses Phänomen ab 1858 und entdeckte, dass schwingende Belastungen ein Bauteil auch dann schädigen können, wenn es durch eine einmalige Belastung mit der gleichen Kraft offensichtlich nicht geschädigt wird.

Die dynamischen Beanspruchungen werden in der Regel als Schwingungen aufgefasst. Eine Radsatzwelle eines Eisenbahnwaggons erfährt beim Rollen beispielsweise eine periodisch schwingende Belastung, da jede Umdrehung einen Lastwechsel darstellt. Aber auch nicht-periodische Belastungen, wie Ein- und Ausschaltvorgänge, können als schwingende Beanspruchung aufgefasst werden.

Wöhlerlinie und Unterscheidung von Kurzzeit-, Zeit- und Dauerfestigkeit

Für die Konstruktion und Dimensionierung eines Bauteils, welches einer schwingenden Belastung unterliegt, muss bekannt sein, wie viele Lastwechsel es überlebt, bevor es zum Bruch kommt. Diese Eigenschaft wird im Wöhlerversuch untersucht, der nach DIN 50100 genormt ist. Hierfür werden die Versuchskörper mit Hochfrequenzpulsatoren zyklisch, meist unter einer sinusförmigen Beanspruchungs-Zeit-Funktion, belastet. Die Beanspruchung kann hierbei je nach Versuchsdurchführung durch Zug-/Druckbelastung, Biegung, Torsion oder Querkraftschub entstehen.[1] Lastamplituden sowie das Spannungsverhältnis aus Unterlast zu Oberlast (der so genannte Ruhegrad $R$ ) sind konstant. Der Versuch läuft, bis ein definiertes Versagen (Bruch, Anriss) eintritt oder eine festgelegte Grenzschwingspielzahl erreicht wird. Versuchskörper, die die Grenzschwingspielzahl ohne erkennbares Versagen erreichen, werden als Durchläufer bezeichnet.

Die maximale Lastwechselanzahl für eine bestimmte Lastamplitude kann aus dem Wöhlerdiagramm abgelesen werden. Sie hängt ab von Werkstoffeigenschaften (zyklisch verfestigend / zyklisch entfestigend), der Kraft beziehungsweise der daraus resultierenden Spannung und der Art der Belastung (schwellende Druckbelastung, schwellende Zugbelastung oder wechselnde Belastung). Bei gleicher Auslenkungsamplitude schädigt die wechselnde Belastung das Bauteil am stärksten.

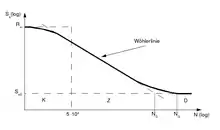
Qualitative Darstellung der Wöhlerlinie mit Kennzeichnung der Bereiche K, Z und D

Üblicherweise wird im Wöhlerdiagramm die Nennspannungsamplitude $S_{a}$ linear oder logarithmisch über der logarithmisch dargestellten, ertragbaren Schwingspielzahl aufgetragen. Den sich ergebenden Kurvenzug nennt man Wöhlerkurve. Weil der Bereich der Zeitfestigkeit in doppeltlogarithmischer Darstellung eine Gerade darstellt, hat sich auch der Begriff Wöhlerlinie etabliert. Betrachtet man eine Wöhlerkurve (rechts), so fallen drei unterschiedliche Bereiche des Graphen auf, die als Kurzzeitfestigkeit K, Zeitfestigkeit Z und Dauerfestigkeit D bezeichnet werden.

K ist der Bereich der Kurzzeitfestigkeit bzw. Kurzzeitschwingfestigkeit (engl. low cycle fatigue, LCF) unterhalb von ca. 10⁴ bis 10⁵ Schwingspielen. Diese Art der Ermüdung tritt bei hohen plastischen Dehnamplituden auf, die zu frühem Versagen führen. Um diesen Bereich genauer darzustellen, wird in der Regel die Coffin-Manson-Auftragung herangezogen. Bei einer Belastung, die innerhalb von einem Viertel Schwingspiel zum Bruch führt, spricht man von der statischen Festigkeit, die auch im Zugversuch bestimmt wird. Für technische Anwendungen hat der Bereich der Kurzzeitfestigkeit lediglich eine geringe Bedeutung.[2]

Z ist der Bereich der Zeitfestigkeit bzw. Zeitschwingfestigkeit, auch Betriebsfestigkeit (engl. high cycle fatigue, HCF) zwischen 10⁴ und materialabhängig etwa 2 · 10⁶ Schwingspielen, in dem die Wöhlerkurve bei doppellogarithmischer Darstellung nahezu gerade verläuft. Die Gerade kann durch die Basquin-Gleichung beschrieben werden.
D ist der anschließende Bereich der so genannten Dauerfestigkeit bzw. Dauerschwingfestigkeit (engl. very high cycle fatigue, VHCF). Bei ferritisch-perlitischen Stählen beginnt der Bereich der Dauerfestigkeit bei zirka 1–5 · 10⁶ Lastwechseln. Es ist aber heute umstritten, ob es überhaupt eine wirkliche Dauerfestigkeit gibt oder ob es bei sehr hohen Lastspielzahlen (engl. ultra high cycle fatigue, UHCF) auch bei sehr geringen Belastungen zum Versagen kommt. Bei austenitischen Stählen und Basiswerkstoffen mit kubisch-flächenzentriertem Kristallgitter (z. B. Aluminium, Gold, Kupfer) fällt die ertragbare Amplitude weiter ab. Eine „echte“ Dauerfestigkeit existiert hier nicht. Daher wird hier meist die ertragbare Amplitude bei 10⁸ Lastwechseln als Dauerfestigkeit bezeichnet. Unterliegt ein Bauteil ständiger Korrosion oder stark erhöhter Temperaturen, so kann nicht mehr mit einer Dauerfestigkeit gerechnet werden.

In der Literatur wird der VHCF oft auch als HCF Bereich dargestellt. Es erfolgt sodann keine Trennung in drei Bereiche, sondern nur in den LCF Bereich und den HCF Bereich (je nach Literatur bereits ab 10⁴ bis 10⁶ Schwingspielen).

Gelegentlich ist auch die Wahrscheinlichkeit, mit der es zum Bruch eines Bauteils kommt, von Interesse. Hierzu wird das Wöhlerdiagramm zu einem dreidimensionalen Koordinatensystem erweitert. Auf den Achsen werden die Größen Ausschlagsspannung, Lastspielzahl und Bruchwahrscheinlichkeit abgetragen, die mathematische Beschreibung erfolgt mit einer Streubandfunktion (SBF). Diese SBF besitzt sechs Konstanten, die aus dem ebenen Wöhlerdiagramm und der Streuung der Dauerfestigkeiten ermittelt werden. Wichtigstes Ergebnis aus der SBF ist die sogenannte Nullbruchlinie, deren Wahrscheinlichkeit mit Hilfe der Vertrauensbereiche individuell eingestellt wird (z. B. 1 ppm, 10 ppm). Mit dieser Auswertung des einstufigen Wöhlerversuches ist es auch möglich, statistisch abgesicherte Aussagen über die Entwicklung der Bruchwahrscheinlichkeit unter mehrstufiger Betriebslast zu machen. Einflüsse der Mittelspannung werden in der Aussage zur Bruchwahrscheinlichkeit berücksichtigt, Einflüsse der Umgebung wie Temperaturschwankungen oder Korrosion müssen meist gesondert betrachtet werden.

Dauerfestigkeit

Unterhalb einer bestimmten maximalen Beanspruchung und ohne das Auftreten zeitabhängiger Schadensmechanismen (wie z. B. Korrosion) können einige Materialien (theoretisch) unendlich viele Schwingungen (Lastwechsel) ertragen. Bauteile, die einem realen Betriebseinsatz unterliegen, zeigen dieses Verhalten nur in Ausnahmefällen und unter bestimmten Voraussetzungen. Meist wird das Bauteil nicht dauerfest, sondern betriebsfest ausgelegt, außerdem zeigen Werkstoffe mit kubisch flächenzentriertem Kristallgitter, darunter viele Nicht-Eisen-Metalle wie Aluminium, keine Grenzschwingspielzahl. Hier ist auch bei geringen Belastungsamplituden bei hohen Lastspielzahlen mit Ermüdungserscheinungen zu rechnen. Gleiches gilt für hochfeste Stähle: So entgleiste im Jahr 2008 ein ICE 3 im Kölner Hauptbahnhof aufgrund eines Bruchs der Radsatzwelle, die mit über 10⁹ Lastwechseln die üblichen Grenzschwingspielzahlen für Dauerfestigkeit weit überschritten hatte.[3]

Die Dauerfestigkeit ist abhängig von der Art der auftretenden Belastung. Je nachdem, ob die Art der Belastung nur aus Druck, Zug und Druck, nur Zug oder zusätzlich auch noch aus Biegung und Torsion besteht, ändert sich ihre jeweilige Höhe. Zusätzlich ist die statische Ruhelast, die sogenannte Mittelspannung, zu beachten. Sie beeinflusst das Werkstoffverhalten enorm. Abhängig von der Mittelspannung spricht man von Wechselfestigkeit oder Schwellfestigkeit:

Die Wechselfestigkeit ist der Dauerfestigkeitswert, bei der die Mittelspannung Null ist.
Die Schwellfestigkeit ist der Dauerfestigkeitswert, bei der die Mittelspannung gleich dem Spannungsausschlag ist.

Dauerfestigkeitsschaubilder

Um die Dauerfestigkeit sowohl in Abhängigkeit von der Mittelspannung als auch in Abhängigkeit von der Ausschlagspannung ablesen zu können, ist die Wöhlerkurve nicht geeignet, da sie stets eine konstante Mittelspannung voraussetzt. Im Laufe der Zeit wurde daher eine Vielzahl an Dauerfestigkeitsschaubildern entwickelt, von denen sich das Haigh-Diagramm und das Smith-Diagramm in der Praxis durchgesetzt haben. Die Anwendung dieser beiden Dauerfestigkeitsschaubilder wird auch in der Norm DIN 50100 empfohlen.[2]

Haigh-Diagramm

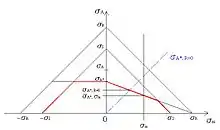
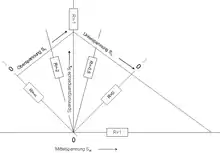
Haigh-Diagramm: Die rot eingezeichnete Kurve umschließt den Bereich der Dauerfestigkeit

Detailskizze der geraden Linien, welche jeweils ein konstantes Spannungsverhältnis R = const. beschreiben, mit je unterschiedlichen Werten von R, wie sie im Haigh-Diagramm vorkommen

Im Haigh-Diagramm wird die Ausschlagspannung $\sigma _{A}$ auf der y-Achse und die Mittelspannung ${\mathcal {}}\sigma _{m}$ auf der x-Achse abgetragen. Zur Konstruktion wird zunächst die Zugfestigkeit ${\mathcal {}}\sigma _{R}$ auf der y-Achse und, sowohl positiv als auch negativ auf der x-Achse eingetragen. Diese drei Punkte bilden das für das Haigh-Diagramm charakteristische gleichschenklige Dreieck. Der Bereich der Dauerfestigkeit wird bestimmt, indem die Wechselfestigkeit ${\mathcal {}}\sigma _{A^{*}}$ und die Streckgrenze ${\mathcal {}}\sigma _{S}$ eingetragen werden. Im Bild links ist der Bereich der Dauerfestigkeit rot gekennzeichnet.

Nun kann für ein beliebiges Spannungsverhältnis die Dauerfestigkeit abgelesen werden. Dazu wird das Spannungsverhältnis $R$ mit

$R={\frac {\sigma _{U}}{\sigma _{O}}}$ gebildet.

Anschließend wird die diesem Spannungsverhältnis zugeordnete Gerade (Beispiele für solche Geraden siehe Bild rechts) bis zur Grenze der Dauerfestigkeit verfolgt.

Smith-Diagramm

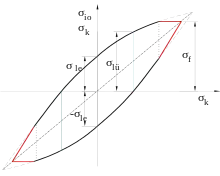
Dauerfestigkeitsschaubild nach Smith

Ein weiteres Dauerfestigkeitsschaubild ist das Dauerfestigkeitsschaubild nach Smith oder kurz Smith-Diagramm.[4] Im Smith-Diagramm wird die Gesamtspannung über der Ausschlagspannung aufgetragen. Zur Konstruktion werden die Streckgrenze, die Quetschgrenze, die Zugschwellfestigkeit, die Druckschwellfestigkeit und die Wechselfestigkeit benötigt. Zunächst wird die Winkelhalbierende eingezeichnet. Die Streckgrenze ist die obere, horizontale Begrenzungslinie des Graphen, die Quetschgrenze die untere Begrenzung. Beide Geraden enden im Schnittpunkt mit der Winkelhalbierenden. Anschließend werden die Werte für Wechselfestigkeit und Schwellfestigkeiten eingetragen und mit Kurven oder Geraden verbunden. Wenn die Amplituden von Ober- oder Unterspannung für die vorliegende Mittelspannung innerhalb des vom Graphen des Smith-Diagramm umschlossenen Bereichs liegen, kann Dauerfestigkeit angenommen werden, andernfalls nicht.

Um teure Werkstoffprüfungen zu umgehen, ist es möglich, empirische Zusammenhänge zwischen den Werkstoffkennwerten zu nutzen. Für die Quetschgrenze und die Druckschwellfestigkeit können für metallische Werkstoffe die entsprechenden Werte für Zugbeanspruchung unter umgekehrtem Vorzeichen verwendet werden, da der Betrag der Druckschwellfestigkeit in der Regel höher ist als der der Zugschwellfestigkeit. Ist die Zugschwellfestigkeit nicht bekannt, kann der Steigungswinkel der Verbindungslinie zwischen Zugschwellfestigkeit und Streckgrenze aus Tabellenwerken entnommen werden. Außerdem existieren Näherungen, die Biegewechselfestigkeit und Streckgrenze, Zug-/Druckwechselfestigkeit und Streckgrenze sowie Biegewechselfestigkeit und Torsionswechselfestigkeit in Zusammenhang setzen.[1]

Betriebsfestigkeit

Oftmals wird ein Bauteil oder eine Baugruppe nicht dauerfest, sondern betriebsfest ausgelegt. Dabei befindet man sich im Bereich der Zeitfestigkeit, wo zwischen der Zugfestigkeit und der Dauerfestigkeit nur eine bestimmte Anzahl an Lastwechseln ertragen wird. Die Zahl der ertragenen Schwingspiele eines Bauteils unter Betriebsbelastung (variable Belastungsamplituden) bis zum Ausfall kann im Rahmen statistischer Genauigkeit mit Hilfe der Wöhlerlinie vorausgesagt werden. Dazu verwendet man die Methoden der linearen Schadensakkumulation nach Palmgren, Langer und Miner. Gleichzeitig werden intensiv experimentelle Erprobungen eingesetzt, um die rechnerischen Ergebnisse zu verifizieren. Betriebsfestigkeit wird heute in nahezu allen Bereichen der Technik zum Zweck des Leichtbaus eingesetzt.

Bauteile, die nicht dauerfest, sondern betriebsfest sind, benötigen weniger Material und haben daher eine geringere Masse. Ein leichteres Fahrzeug hat beispielsweise einen geringeren Treibstoffverbrauch, eine leichtere Struktur erlaubt eine höhere Nutzlast. Gelegentlich dient die betriebsfeste Auslegung auch der Erfüllung der Funktion: Dauerfeste Flugzeuge würden nicht fliegen können, weil sie zu schwer wären.

In die Betrachtung der Betriebsfestigkeit fließen in der Realität auch schlag- und stoßartige Belastungen sowie Umgebungsbedingungen wie Temperatur, Druck, Korrosion, Steinschläge, Niederschlag, Kriechen und Alterung des Materials. Wichtig ist auch die Unterscheidung zwischen zweckorientiertem Betrieb und Missbrauch. Ein betriebsfestes Bauteil ist nur bis zu einer bestimmten Schwingungs- oder Schlagamplitude ausgelegt und darf nach dem Überschreiten dieser Grenzbelastung versagen. Idealerweise versagt ein sicherheitsrelevantes Bauteil lediglich durch Verformung und nicht durch Bruch, um eine Restsicherheit zu gewährleisten und ein Unfallrisiko zu verringern. Sonderereignisse spielen in der Erprobung von Bauteilen eine große Rolle, da diese Beanspruchungen vom betriebsfesten Bauteil schadensfrei ertragen werden müssen. Diese Belastungen kommen jedoch innerhalb der kalkulierten Lebensdauer nur im Ausnahmefall vor und fallen durch die mittlere Amplitudenstärke nicht unter Missbrauch.

Gestaltfestigkeit

Kerben, wie diese Bohrung, führen zu Spannungskonzentrationen, die die Gestaltfestigkeit verringern

Die Schwingfestigkeit eines konkreten Bauteils wird als Gestaltfestigkeit bezeichnet. Sie liegt in der Praxis deutlich unterhalb der im Wöhlerversuch für eine genormte Probe ermittelten Dauerfestigkeit oder Zeitfestigkeit. Dies hat mehrere Gründe:

Je größer ein Bauteil ist, desto geringer ist seine Gestaltfestigkeit. Bei metallischen Werkstoffen können herstellungsbedingte nichtmetallische Einschlüsse zur Rissbildung führen. Bei größeren Bauteilen ist die absolute Zahl der Einschlüsse oder Werkstofffehler höher. Somit steigt auch die Wahrscheinlichkeit, dass eine dieser Fehlstellen zu einem voranschreitenden Riss wird, der einen Bruch nach sich ziehen kann. Eine Welle mit einem Durchmesser von 60 mm kann bei Dauerfestigkeit eine 20 % geringere Ausschlagsspannung als eine Welle mit einem Durchmesser von 10 mm aushalten.[5]
Raue Oberflächen verringern die ertragbare schwingende Beanspruchung. Die im Wöhlerversuch ermittelten Werte entsprechen polierten Oberflächen. Ist eine Oberfläche lediglich geschruppt oder mit einer Walzhaut versehen, können an Kanten der Oberfläche Risse entstehen, die bei jedem Lastwechsel wachsen und so das Bauteil durchdringen. Besonders stark ausgeprägt ist dieser Effekt bei hochfesten Stählen, die eine hohe Zugfestigkeit aufweisen, aber zum Sprödbruch neigen. Hier ist die ertragbare Ausschlagspannung der polierten Oberfläche im Vergleich zur Oberfläche des Halbzeugs teilweise doppelt so groß.[5]
Reale Bauteile enthalten Kerben, beispielsweise durch Freistiche oder Wellenabsätze. Diese Kerben führen zu unerwünschten Spannungsspitzen. Bei der Bestimmung der zulässigen Spannungen muss daher eine Multiplikation mit der Kerbwirkungszahl erfolgen.[5]

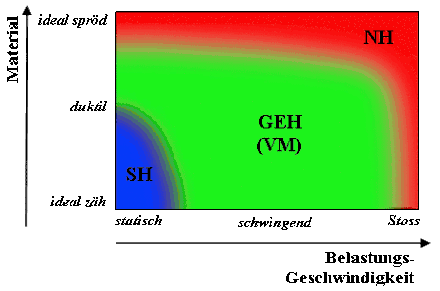
Die Gestaltänderungsenergie- hypothese deckt den Bereich der schwingenden Beanspruchung ab

Während im Wöhlerversuch ein einachsiger Spannungszustand mit Zug-/Druckbelastung vorliegt, sind in der Realität mehrachsige Spannungszustände mit Biegung, Torsion und Querkraftschub zu betrachten. Um die Versuchsergebnisse der Werkstoffprüfung weiterhin nutzen zu können, muss die Vergleichsspannung für das jeweilige Bauteil berechnet werden. Bei schwingender Beanspruchung ist dabei die Gestaltänderungsenergiehypothese (GEH) das am häufigsten verwendete Werkzeug.[5]

Ist ein konkretes Bauteil dauerfest, so spricht man von Gestaltdauerfestigkeit. Als Gestaltdauerfestigkeitsschaubild wird in der Regel ein Smith-Diagramm verwendet, in das Reduktionen des sicheren Bereichs aufgrund von Größen- und Oberflächeneinfluss sowie Kerbwirkungszahl eingetragen werden.[5]

Für in Serienfertigung hergestellte Komponenten sowie sicherheitsrelevante Bauteile wie Drehgestelle werden als Festigkeitsnachweis Bauteil-Wöhlerversuche durchgeführt.[6]

Schwingfestigkeitsverbesserung bei Schweißkonstruktionen

Beispiel einer mittels hochfrequenten Hämmerns nachbehandelten Schweißkonstruktion

Die Betriebsfestigkeit und Lebensdauer schwingend belasteter geschweißter Metallkonstruktionen wird in vielen Fällen durch die Schweißnähte – insbesondere die Schweißnahtübergänge – bestimmt. Durch gezielte Nachbehandlung der Übergänge durch Schleifen, Strahlen, Kugelstrahlen, hochfrequentes Hämmern etc. kann die Lebensdauer mit einfachen Mitteln bei vielen Konstruktionen erheblich gesteigert werden. Beim hochfrequenten Hämmern basiert die Steigerung der Schwingfestigkeit im Wesentlichen auf dem Einbringen von Druckeigenspannungen zur Erhöhung des Widerstandes gegen Rissbildung und Rissausbreitung durch Überlagerung der Kerbspannungen mit Druckeigenspannungen, einer Reduzierung der Kerbwirkung und einer Verfestigung der Randschicht.

Literatur

E. Haibach: Betriebsfestigkeit, Springer-Verlag Berlin, 3. Auflage, 2006
S. Götz, K.-G. Eulitz: Betriebsfestigkeit, Springer Vieweg, 2020
J. Köhler: Nullbruchlinie der Dauerfestigkeit. In: Materialwissenschaft und Werkstofftechnik. Band 39, Nr. 9, 2008, S. 654–658, doi:10.1002/mawe.200800326.
J. Köhler: Relative Dauerfestigkeit, De Gruyter Oldenbourg Verlag, 2014
D. Munz, K. Schwalbe, P. Mayr: Dauerschwingverhalten metallischer Werkstoffe. Braunschweig 1971

Weblinks

Bilder von Versuchen zur Schwingfestigkeit auf der Webseite des IWM der RWTH Aachen
Video der Hochschule Karlsruhe - Technik und Wirtschaft zur Schwingfestigkeitsprüfung auf YouTube

Einzelnachweise

Georg Jacobs: Maschinengestaltung. Mainz Verlag, Aachen 2015, ISBN 3-86130-748-0, S. 19–21.
Christoph Broeckmann, Paul Beiss: Werkstoffkunde I. Mainz Verlag, Aachen 2014, S. 40–54.
Bundesanstalt für Materialforschung und -prüfung: Schadensanalyse Radsatzwelle ICE 3 auf bahn-fuer-alle.de, abgerufen am 22. November 2015.
Dauerfestigkeitsschaubild nach Smith Konstruktion des Smith-Diagramms
Georg Jacobs: Maschinengestaltung. Mainz Verlag, Aachen 2015, ISBN 3-86130-748-0, S. 24–42.
Heiko Mannsbarth, Jürgen Jakob: Drehgestell Görlitz IX – konsequente Weiterentwicklung bewährter Drehgestell-Technologie. (Memento des Originals vom 8. Dezember 2015 im Internet Archive) Info: Der Archivlink wurde automatisch eingesetzt und noch nicht geprüft. Bitte prüfe Original- und Archivlink gemäß Anleitung und entferne dann diesen Hinweis.@1@2 In: Glasers Annalen 132 (Oktober 2008), abgerufen am 30. Oktober 2015.

Siehe auch

Pneumatic Impact Treatment, ein HFMI Verfahren zur signifikanten Steigerung der Schwingfestigkeit

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[:1-1] Georg Jacobs: Maschinengestaltung. Mainz Verlag, Aachen 2015, ISBN 3-86130-748-0, S. 19–21.

[:0-2] Christoph Broeckmann, Paul Beiss: Werkstoffkunde I. Mainz Verlag, Aachen 2014, S. 40–54.

[3] Bundesanstalt für Materialforschung und -prüfung: Schadensanalyse Radsatzwelle ICE 3 auf bahn-fuer-alle.de, abgerufen am 22. November 2015.

[Smith-4] Dauerfestigkeitsschaubild nach Smith Konstruktion des Smith-Diagramms

[jacobs-gestalt-5] Georg Jacobs: Maschinengestaltung. Mainz Verlag, Aachen 2015, ISBN 3-86130-748-0, S. 24–42.

[zevrail-6] Heiko Mannsbarth, Jürgen Jakob: Drehgestell Görlitz IX – konsequente Weiterentwicklung bewährter Drehgestell-Technologie. (Memento des Originals vom 8. Dezember 2015 im Internet Archive) Info: Der Archivlink wurde automatisch eingesetzt und noch nicht geprüft. Bitte prüfe Original- und Archivlink gemäß Anleitung und entferne dann diesen Hinweis.@1@2 In: Glasers Annalen 132 (Oktober 2008), abgerufen am 30. Oktober 2015.