Punktoperator (Bildverarbeitung)

Als Punktoperatoren bezeichnet man eine umfangreiche Klasse von Bildverarbeitungsoperationen in der digitalen Bildverarbeitung, die sich – gegenüber lokalen und globalen Operatoren – dadurch auszeichnen, dass bei allen Verfahren dieser Klasse ein neuer Farb- oder Grauwert eines Pixels allein in Abhängigkeit von seinem eigenen bisherigen Farb- oder Grauwert und seiner eigenen bisherigen Position im Bild berechnet wird, ohne sich dabei um seine Nachbarschaft und/oder den Kontext des Pixels zu kümmern.

Einordnung

Unter dem Oberbegriff der Punktoperatoren finden sich verschiedene häufig genutzte Verfahren der digitalen Bildverarbeitung wie Tonwertkorrektur, Kontrastverstärkung, Helligkeitskorrektur usw. sowie Visualisierung zusammengefasst, und dementsprechend weit gefächert ist auch das Einsatzgebiet von Punktoperatoren in einem typischen Bildverarbeitungssystem:

Szene

→

Bildaufnahme

→

Vorverarbeitung

→

Segmentierung

→

Merkmalsextraktion

→

Klassifizierung

→

Bildverstehen
Visualisierung

Sie stellen meistens den ersten Schritt der Vorverarbeitung dar, um den Bildkontrast zu verstärken oder Belichtungsfehler bei der Bildaufnahme auszugleichen. Die Segmentierung eines Bildes wird oft durch die Anwendung eines globalen Schwellwertverfahrens realisiert. Im Anschluss an die Segmentierung werden die gefundenen Objekte oft noch klassifiziert, d. h. in einzelne Klassen „einsortiert“. Bei der Visualisierung der Ergebnisse einer Segmentierung oder einer Klassifizierung für den Menschen sind die Verfahren der Pseudokolorierung oder Falschfarbendarstellung gebräuchlich.

Neben den Punktoperatoren, die jedes Pixel eines Bildes einzeln transformieren, gibt es in der digitalen Bildverarbeitung mit den lokalen Operatoren und den globalen Operatoren zwei weitere Klassen von Bildverarbeitungsoperationen. Lokale Operatoren berechnen einen neuen Farb- oder Grauwert eines Pixels immer auf Basis einer Nachbarschaft oder einer örtlich begrenzten Region um das Pixel. Hier seien als Beispiele Rangordnungsoperatoren oder morphologische Operatoren genannt. Globale Operatoren betrachten für die Transformation eines jeden Pixels immer das gesamte Bild, was beispielsweise bei der Fourier-Transformation der Fall ist.

Die meisten Punktoperatoren gehören der Klasse der Low-Level-Operatoren an. In dieser Klasse sind alle primitiven Vorverarbeitungsoperationen, wie beispielsweise Rauschunterdrückung oder Kontrastverbesserung, zusammengefasst. Einen Low-Level-Operator zeichnet aus, dass sowohl die Eingabe als auch die Ausgabe ein Bild ist. Im Gegensatz dazu stehen die Mid-Level-Operatoren, die eine Segmentierung eines Bildes berechnen und Merkmale der Segmente extrahieren, und die High-Level-Operatoren, die das Zusammenspiel der erkannten Objekte im Bild analysieren und das Bild zu verstehen versuchen.

Allgemeine Definition

Ein Punktoperator T ordnet einem Eingabebild f durch Transformation der Grauwerte der einzelnen Pixel ein Ergebnisbild f* zu. Der Grauwert f(x,y) eines Pixels (x,y) wird dabei nur in Abhängigkeit vom Grauwert selbst und eventuell von der Position des Pixels im Bild modifiziert:

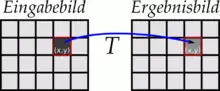
Transformation des Grauwerts im Pixel (x,y)

f^{*}(x,y)=T_{xy}(f(x,y))\,

Ist die Transformation von der Position des Pixels im Bild abhängig, so heißt sie inhomogen. Die Indizes x und y von T sollen diese Abhängigkeit verdeutlichen. In der Mehrheit der Fälle kommen jedoch homogene Transformationen zum Einsatz, bei denen diese Abhängigkeit nicht gegeben ist. Die Indizes werden dann überflüssig:

f^{*}(x,y)=T(f(x,y))\,

Über die Umkehrbarkeit solcher Transformationen lässt sich keine allgemeingültige Aussage treffen. Einige im Folgenden vorgestellte Verfahren, wie z. B. die Negativtransformation, sind ohne Einschränkungen umkehrbar. Einige weitere Verfahren, wie z. B. die Histogrammspreizung, sind umkehrbar, solange eine kontinuierliche Grauwertskala vorliegt. Werden jedoch die in der Praxis gebräuchlichen diskreten Grauwerte verwendet (siehe Abschnitt Anwendung), treten Rundungsfehler auf und die Transformationen sind aus streng mathematischer Sicht nicht mehr umkehrbar. Meistens wirken sich die Rundungsfehler nur sehr gering aus und da das menschliche Auge den feinen Unterschied zwischen zwei benachbarten Grauwerten im Normalfall nicht wahrnehmen kann, ergibt die Umkehrung der Transformation subjektiv wieder das Originalbild. Schließlich gibt es einige Verfahren, wie z. B. die Histogrammbegrenzung, die nicht umkehrbar sind, da bei der Anwendung Informationen unwiederbringlich verloren gehen.

Ein Punktoperator kann auch als ein Operator auf einer Nachbarschaft der Größe 1×1, also einem einzigen Pixel, aufgefasst werden und stellt daher die einfachste Form eines Nachbarschaftsoperators dar.

Anwendung

In der Praxis ist das Eingabebild einer Operation in den meisten Anwendungsfällen ein Grauwertbild mit diskretem Definitionsbereich $\lbrace 0,\ldots ,G\rbrace$ . Der Wert „0“ steht hierbei für „Schwarz“, der Wert „G“ für „Weiß“. G stellt also den größten möglichen Grauwert dar und berechnet sich für ein Bild der Farbtiefe n Bit nach der Formel:

G=2^{n}-1\,

Für n = 8 Bit, n = 12 Bit oder n = 16 Bit, den drei häufigsten Grauwertbild-Formaten, beträgt G demnach 255, 4095 bzw. 65535.

Die Alternative zu einer diskreten Grauwertskala ist eine kontinuierliche Skala. In einem solchen Bild gibt es theoretisch unendlich viele Grauwerte, die durch Gleitkommazahlen, gewöhnlich im Wertebereich $\lbrack 0,1\rbrack$ , dargestellt werden. Der Ausdruck „im Diskreten“ bedeutet, dass dem Bild eine diskrete Grauwertskala zugrunde liegt, während „im Kontinuierlichen“ eine kontinuierliche Skala bezeichnet.

Bei der Anwendung eines homogenen Punktoperators auf ein Bild mit diskreter Skala wird die Transformation in der Praxis oftmals nicht für jedes Pixel einzeln berechnet. Es genügt, jeden möglichen Grauwert einmal zu transformieren und in einer sogenannten Lookup-Tabelle zu speichern. Das Transformationsergebnis für jedes Pixel muss dann nur noch in der Tabelle nachgeschlagen werden.

Beispiel: Ein Bild der Größe 640 × 480 besteht aus 307.200 Pixeln. Anstatt über 300.000 Grauwerte zu transformieren, kommt man bei einer Farbtiefe von beispielsweise 12 Bit mit 4096 Transformationen für alle Werte der Lookup-Tabelle aus. Hinzu kommen allerdings noch 307.200 Lesezugriffe auf die Tabelle. Bei einfacheren Verfahren, wie z. B. der Negativtransformation, bei der nur eine simple Subtraktion ausgeführt wird, benötigt die Transformation eines Pixels weniger Rechenzeit als das Nachschlagen in der Tabelle. Die Verwendung von Lookup-Tabellen lohnt sich also nur bei rechenintensiveren Transformationen wie beispielsweise der Histogrammspreizung.

Da bei homogenen Punktoperatoren die Verwendung einer Lookup-Tabelle prinzipiell immer möglich ist, kann die im vorherigen Abschnitt definierte Transformation T des Grauwerts f(x,y) eines Pixels (x,y) nach f*(x,y) allgemeiner als Transformation eines Grauwerts g nach g* formuliert werden:

g^{*}=T(g)\,

{\text{mit}}

T:\lbrace 0,\ldots ,G\rbrace \rightarrow \lbrace 0,\ldots ,G\rbrace \quad {\text{im Diskreten}}

$T:\lbrack 0,1\rbrack \rightarrow \lbrack 0,1\rbrack \quad {\text{im Kontinuierlichen}}$

Histogramm mit Transformationskennlinie

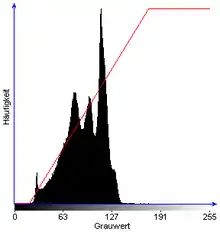
Die homogene Abbildung der Grauwerte g des Eingabebildes auf die Grauwerte g* im Ergebnisbild kann durch eine sogenannte Transformationskennlinie beschrieben werden, die im Diskreten durch die Lookup-Tabelle gegeben ist. Sie ist im Allgemeinen nicht linear, aber monoton über ihrem Definitionsbereich, der Grauwertskala, die gleichzeitig ihren Wertebereich darstellt. Im Bereich der digitalen Bildbearbeitung wird die Transformationkennlinie Gradationskurve genannt.

Die statistischen Häufigkeiten der einzelnen Grauwerte im Eingabe- und im Ergebnisbild können mit Hilfe von Histogrammen grafisch dargestellt werden. Sie ermöglichen Aussagen über die vorkommenden Grauwerte, den Kontrastumfang und die Helligkeit eines Bildes und die Güte einer möglichen Bildsegmentierung bei Anwendung eines Schwellwertverfahrens.

Das Abbildungsverhalten eines Punktoperators kann anschaulich anhand eines Grauwerthistogramms des Eingabebildes dargestellt werden, das mit der verwendeten Transformationskennline überlagert wird. Diese Darstellungsform hat den Vorteil, dass man relativ leicht ablesen kann, welcher Grauwert des Eingabebildes auf welchen Grauwert im Ergebnisbild abgebildet wird (siehe nebenstehendes Beispiel).

Fast alle im Folgenden vorgestellten Verfahren sind im Prinzip auch auf Farbbilder anwendbar. Eine Möglichkeit besteht darin, aus den einzelnen Farbkanälen eines Bildes ein gemeinsames Grauwertbild zu berechnen und dieses mit dem gewünschten Punktoperator zu transformieren. Das Ergebnis ist in diesem Fall allerdings selbst ein Grauwertbild. Etwas komplizierter wird es, wenn das Ergebnisbild wieder ein Farbbild sein soll. Denn eine Transformation jedes einzelnen Farbkanals, beispielsweise des roten, grünen und blauen Kanals bei Verwendung des RGB-Farbraums, führt zu unschönen bis falschen Ergebnissen. Abhilfe schafft hier eine Umrechnung des RGB-Bildes in das YCbCr-Farbmodell. Der Y-Kanal, der die Helligkeit wiedergibt, kann nun wie ein Grauwertbild transformiert werden. Anschließend muss das Bild dann wieder in den RGB-Farbraum zurückgerechnet werden.

Homogene Standardtransformationen

Vergleich der Transformationskennlinien von Potenz-, Logarithmus-, Exponential- und Negativtransformationen

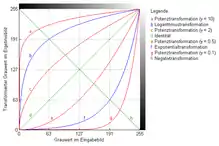
Im Folgenden sollen einige homogene Punktoperatoren vorgestellt werden, die in der digitalen Bildverarbeitung, einige davon auch in der digitalen Bildbearbeitung, vielfach Anwendung finden.

Die meisten homogenen Transformationen lassen sich in zwei Klassen einteilen: Zur ersten Klasse zählen die Verfahren, deren Transformationskennlinien immer gleich aussehen, egal auf welches Bild sie angewendet werden. Dazu zählen die Negativtransformation, die Potenztransformation, die Logarithmustransformation und die Exponentialtransformation (für einen Vergleich siehe nebenstehende Abbildung). Zur zweiten Klasse lassen sich die Verfahren zusammenfassen, deren Transformationskennlinien auf Basis des Grauwerthistogramms des Eingabebildes berechnet werden, also die Histogrammverschiebung, die Histogrammspreizung, die Histogrammbegrenzung und die Histogrammäqualisation. Lediglich die Schwellwertverfahren sowie die Pseudokolorierung lassen sich in diese Klassifikation nicht einordnen.

Ohne Beschränkung der Allgemeinheit wird im Folgenden für alle Bilder angegommen, dass sie Grauwertbilder mit einem diskreten Wertebereich $\lbrace 0,\ldots ,G\rbrace$ sind. Alle vorgestellten Verfahren sind auch auf Gleitkomma-Grauwertbilder anwendbar. In diesem Fall entfallen die Rundungen und die Normalisierungsfaktoren müssen ggf. angepasst werden.

Negativtransformation

Die Invertierung der Grauwerte eines Grauwertbildes heißt Negativtransformation. Da das menschliche visuelle System feine Unterschiede zwischen Grauwerten in verschiedenen Helligkeitsbereichen unterschiedlich gut wahrnimmt, kann eine Negativtransformation zur besseren Wahrnehmung feiner Strukturen führen. Das Ergebnisbild ist ein Negativ, wie es aus der analogen Fotografie bekannt ist. Es kann leicht berechnet werden, indem für jedes Pixel eine einfache Subtraktion ausgeführt wird:

T_{\mathrm {neg} }(g)=G-g.\,

Diese Transformation ist im Gegensatz zu den meisten anderen sowohl im Kontinuierlichen als auch im Diskreten ohne Einschränkung durch nochmalige Anwendung umkehrbar:

T_{\mathrm {neg} }(T_{\mathrm {neg} }(g))=G-(G-g)=G-G+g=g.\,

Beispielbild: Mikrokalkablagerungen in einer weiblichen Brust (Mammografie-Aufnahme)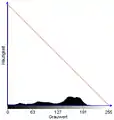
Histogramm mit Transformationskennlinie
Bild nach Negativtransformation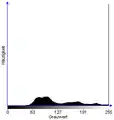
Histogramm

Potenztransformation

Die Potenztransformation (auch Gammakorrektur genannt) ist eine monotone Transformation auf Basis einer Potenzfunktion. Mit diesem Verfahren lässt sich die Helligkeit eines Bildes verändern, indem für einen Teil der Grauwerte eine nichtlineare Spreizung durchgeführt wird, während der andere Teil nichtlinear gestaucht wird.

Der Parameter $\gamma$ spezifiziert das genaue Verhalten der Transformation. Wird $\gamma <1$ gewählt, so bildet die Transformation eine kleine Anzahl Grauwerte am unteren Ende der Skala auf einen größeren Wertebereich ab (der Bereich wird gespreizt), während die restlichen Grauwerte auf einen entsprechend kleineren Bereich projiziert werden (dieser Bereich wird gestaucht). Das Bild wird dadurch im Ergebnis aufgehellt. Dieses Verhalten ist umso stärker ausgeprägt, je kleiner $\gamma$ ist. Wird $\gamma >1$ gewählt, so verhält sich die Transformation genau entgegengesetzt. Eine große Anzahl Grauwerte am unteren Ende der Skala wird dann also gestaucht und eine entsprechen kleinere Anzahl am oberen Ende der Skala gespreizt. Hierdurch wird das Bild umso stärker abgedunkelt, je größer $\gamma$ ist. Der Spezialfall $\gamma =1$ stellt die Identitätsfunktion dar, d. h. das Bild wird durch die Transformation nicht verändert. Die Transformationskennlinien für verschiedene Parameter $\gamma$ sind in der Abbildung weiter oben dargestellt.

Da die Transformation auf den Wertebereich $\lbrack 0,1\rbrack$ angewendet werden muss, werden die Grauwerte g zuerst mittels Division durch G auf diesen normalisiert. Nach der Potenzierung mit dem Exponenten $\gamma$ wird das Ergebnis durch Multiplikation mit G und einer Rundung wieder auf gewünschten Bereich $\lbrace 0,\ldots ,G\rbrace$ normalisiert:

T_{\text{power}}(g)=\left\lbrack G\cdot \left({\frac {g}{G}}\right)^{\gamma }\right\rbrack

Die Umkehrung der Potenztransformation ist im Kontinuierlichen ohne Einschränkung durch eine nochmalige Anwendung mit dem Kehrwert des Parameters $\gamma$ möglich. Im Diskreten kann sie allerdings aufgrund der Rundungsfehler nur annähernd berechnet werden:

T_{\text{power}}^{-1}(g)=\left\lbrack G\cdot \left({\frac {g}{G}}\right)^{\frac {1}{\gamma }}\right\rbrack

Die Potenztransformation bietet die Möglichkeit, Grauwert- oder Farbkennlinien von technischen Geräten (z. B. Digitalkamera oder Monitor) zu manipulieren. Das ist notwendig, um das Aufnahme- oder Abbildungsverhalten von Grau- oder Farbwerten der einzelnen Geräte aneinander anzupassen. Auf diese Art und Weise kann auch das Helligkeitsprofil eines Monitors an das logarithmische Helligkeitsempfinden des menschlichen visuellen Systems angepasst werden.


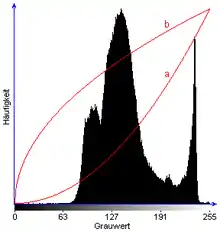Histogramm mit Transformationskennlinien	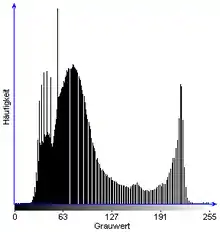Histogramm a	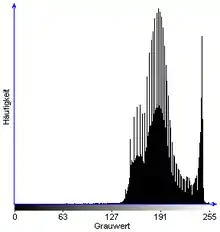Histogramm b

Logarithmustransformation

Die Logarithmustransformation ist eine monotone Transformation auf Basis des Logarithmus. Sie bildet eine kleine Grauwertspanne im unteren Bereich der Skala im Eingabebild auf eine größere Grauwertspanne im Ergebnisbild ab, während die oberen Grauwerte der Skala komprimiert werden. Dadurch wird das Bild insgesamt aufgehellt.

Da $\log(0)=-\infty$ , muss der Wertebereich $\lbrace 0,\ldots ,G\rbrace$ der Grauwerte g vor dem Logarithmieren durch Addition von 1 zunächst auf den Bereich $\lbrace 1,\ldots ,G+1\rbrace$ abgebildet werden. Um von der Logarithmusfunktion ein Ergebnis im Intervall $\lbrack 0,1\rbrack$ zu erhalten, wird folglich als Basis $G+1$ benutzt. Die Multiplikation mit G und die Rundung normalisiert das Ergebnis schließlich wieder auf den gewünschten Bereich $\lbrace 0,\ldots ,G\rbrace$ :

T_{\mathrm {log} }(g)=T_{\mathrm {exp} }^{-1}(g)=\left\lbrack G\cdot {\frac {\log _{2}(g+1)}{\log _{2}(G+1)}}\right\rbrack =\left\lbrack G\cdot \log _{(G+1)}(g+1)\right\rbrack

Die zugehörige Transformationskennlinie ist in einer Abbildung weiter oben dargestellt. Die Umkehrung der Logarithmustransformation ist im Kontinuierlichen ohne Einschränkung durch Anwendung der Exponentialtransformation möglich. Im Diskreten kann sie allerdings aufgrund der Rundungsfehler nur annähernd berechnet werden.

Die Logarithmustransformation wird häufig nach einer Fouriertransformation eines Bildes zwecks Visualisierung auf das Powerspektrum angewendet. In solchen Spektren gibt es oft einzelne Punkte, die eine um viele Zehnerpotenzen höhere spektrale Dichte haben als die restlichen. Eine einfache Normierung aller Werte auf den Bereich $\lbrace 0,\ldots ,G\rbrace$ hätte in einem solchen Fall zur Folge, dass diese herausragenden Punkte mit Wert G und alle restlichen Punkte mit Wert 0 dargestellt würden (siehe Beispiel unten). Durch die Logarithmustransformation werden die hohen Dichten so weit abgeschwächt, dass in dem Spektrum nach einer Normalisierung tatsächlich etwas zu erkennen ist. Zu beachten ist, dass bei dieser Anwendung die maximale vorkommende Dichte als Basis des Logarithmus benutzt werden muss. Im Gegensatz zu oben entfällt die Addition von 1, und falls die Dichte eines Punktes den Wert 0 haben sollte, so muss sie anstelle einer Logarithmierung einfach auf 0 abgebildet werden.

Beispielbild

Fourierspektrum des Bildes mit Wertebereich [0, 2e+09] auf den Bereich {0,...,255} normiert

Fourierspektrum des Bildes nach Logarithmustransformation auf den Bereich {0,...,255} normiert

Exponentialtransformation

Die Exponentialtransformation ist eine monotone Transformation auf Basis der Exponentialfunktion. Sie bildet eine kleine Grauwertspanne im oberen Bereich der Skala im Eingabebild auf eine größere Grauwertspanne im Ergebnisbild ab, während die unteren Grauwerte der Skala komprimiert werden. Dadurch wird das Bild insgesamt abgedunkelt.

Die Division durch G normalisiert die Grauwerte g auf den Wertebereich $\lbrack 0,1\rbrack$ . Der Wertebereich der Potenzfunktion $\lbrace 1,\ldots ,G+1\rbrace$ wird durch die Subtraktion von 1 auf den gewünschten Bereich $\lbrace 0,\ldots ,G\rbrace$ abgebildet:

T_{\mathrm {exp} }(g)=T_{\mathrm {log} }^{-1}(g)=\left\lbrack (G+1)^{\frac {g}{G}}-1\right\rbrack

Die zugehörige Transformationskennlinie ist in einer Abbildung weiter oben dargestellt. Die Umkehrung dieser Transformation ist im Kontinuierlichen ohne Einschränkung durch Anwendung der Logarithmustransformation möglich. Im Diskreten kann sie allerdings aufgrund der Rundungsfehler nur annähernd berechnet werden.

Histogrammverschiebung

Die Histogrammverschiebung ist ein einfaches Verfahren zur Regulierung der Helligkeit eines Bildes. Dabei werden alle Grauwerte g des Bildes um eine feste Konstante c auf der Grauwertskala in den hellen oder dunklen Bereich verschoben:

T_{\text{trans}}(g)={\begin{cases}0&{\text{falls }}g+c<0\\g+c&{\text{falls }}0\leq g+c\leq G\\G&{\text{falls }}g+c>G\end{cases}}

Die Histogrammverschiebung ist nicht umkehrbar, da immer Grauwerte aus der Skala „hinausgeschoben“ werden. Eine Ausnahme stellt der Fall dar, wenn der hinausgeschobene Grauwertbereich im Bild ungenutzt war.

Beispielbild: Das Erechteum auf der Akropolis in Athen
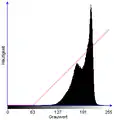Histogramm mit Transformationskennlinie
Bild nach Histogrammverschiebung mit c = -64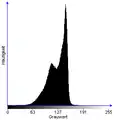
Histogramm

Histogrammspreizung und -stauchung

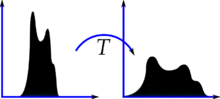
Schematische Darstellung der Histogrammspreizung

Die Histogrammspreizung, auch Tonwertspreizung genannt, ist ein häufig eingesetztes Verfahren zur Kontrastverstärkung in kontrastarmen Grauwertbildern. In solchen Bildern kommen viele Grauwerte der Grauwertskala überhaupt nicht vor. Je größer die ungenutzten Bereiche an den beiden Rändern der Skala sind, desto stärker kann der Abstand zwischen dem dunkelsten und dem hellsten Grauwert vergrößert werden, desto weiter können also die Grauwerte im Bild „auseinandergezogen“ werden.

Die Berechnung einer Grauwertspreizung geschieht mittels einer stückweise linearen Transformation, die den benutzten Grauwertbereich $\lbrace g_{\mathrm {min} },\ldots ,g_{\mathrm {max} }\rbrace$ auf den gesamten verfügbaren Bereich $\lbrace 0,\ldots ,G\rbrace$ abbildet:

T_{\text{stretch}}(g)=\left\lbrack G\cdot {\frac {g-g_{\mathrm {min} }}{g_{\mathrm {max} }-g_{\mathrm {min} }}}\right\rbrack

Die Umkehrung der Histogrammspreizung, die Histogrammstauchung (Tonwertreduktion), ist im Kontinuierlichen ohne Einschränkung möglich. Im Diskreten kann sie allerdings aufgrund der Rundungsfehler nur annähernd berechnet werden. Sie verringert den Kontrast im Bild, indem sie die Grauwerte im Bild näher „zusammenschiebt“. Im Diskreten wird dabei die Anzahl der benutzten Grauwerte verringert, da nebeneinander liegende Grauwerte auf einen einzigen Grauwert abgebildet werden. Aufgrund dieses Informationsverlustes ist die Histogrammstauchung im Diskreten nicht umkehrbar. Sie findet in der digitalen Bildverarbeitung eher selten Anwendung.

Beispielbild
Histogramm mit Transformationskennlinie
Bild nach Histogrammspreizung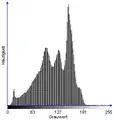
Histogramm

Histogrammbegrenzung

Ist in einem Grauwertbild eine differenzierte Betrachtung eines bestimmten Grauwertbereichs gewünscht, so kann eine Histogrammbegrenzung durchgeführt werden. Dabei werden die Grauwerte unterhalb und oberhalb dieses Bereichs $(\lbrace 0,\ldots ,g_{\text{min}}-1\rbrace$ bzw. $\lbrace g_{\text{max}}+1,\ldots ,G\rbrace )$ „abgeschnitten“, indem sie auf 0 (schwarz) bzw. G (weiß) abgebildet werden. Die verbleibenden Grauwerte $\lbrace g_{\text{min}},\ldots ,g_{\text{max}}\rbrace$ werden dann durch ein geeignetes Verfahren, typischerweise eine Histogrammspreizung, kontrastverstärkt:

T_{\text{clip}}(g)={\begin{cases}0&{\text{falls }}0\leq g<g_{\text{min}}\\T_{\text{stretch}}(g)&{\text{falls }}g_{\text{min}}\leq g\leq g_{\text{max}}\\G&{\text{falls }}g_{\text{max}}<g\leq G\end{cases}}

Die Histogrammbegrenzung ist offensichtlich mit einem Informationsverlust verbunden, da sie im Normalfall viele Grauwerte auf schwarz oder weiß abbildet. Daher ist sie nicht umkehrbar.

Beispielbild: Das Erechteum auf der Akropolis in Athen
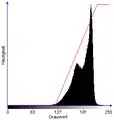Histogramm mit Transformationskennlinie
Bild nach Histogrammbegrenzung und -spreizung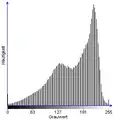
Histogramm

Histogrammäqualisation

Schematische Darstellung der Histogrammäqualisation

Die Histogrammäqualisation (auch Histogrammausgleich, Histogrammeinebnung, Histogrammegalisierung oder Histogrammequalisierung genannt) ist ein wichtiges Verfahren zur Kontrastverbesserung in Grauwertbildern, das über eine bloße Kontrastverstärkung hinausgeht. Dabei wird aus der Grauwertverteilung im Histogramm eine Gleichverteilung berechnet, damit der gesamte zur Verfügung stehende Wertebereich optimal ausgenutzt wird.

Diese Methode kommt besonders in solchen Fällen zur Anwendung, bei denen die interessanten Bildbereiche einen relativ großen Teil des Bildes ausmachen (die entsprechenden Grauwerte also überdurchschnittlich häufig vorkommen) und ihre Grauwerte auf einen kleinen Bereich der Grauwertskala begrenzt sind.

Im Gegensatz zu einer Histogrammbegrenzung mit anschließender Histogrammspreizung, wo zwar der Kontrast im interessanten Grauwertbereich verstärkt wird, die Informationen außerhalb des Bereichs allerdings komplett verloren gehen, werden bei der Histogrammäqualisation häufige Grauwerte „auseinandergezogen“ (die Grauwertskala wird in diesen Bereichen gestreckt) und weniger häufige Grauwerte „zusammengeschoben“ (die Grauwertskala wird in diesen Bereichen gestaucht).

Eine so schöne Gleichverteilung wie in der nebenstehenden schematischen Darstellung wird in der Praxis jedoch nie erreicht werden. Das Histogramm des Ergebnisbildes wird vielmehr mehr oder weniger große Lücken enthalten (siehe Beispiel unten). Das rührt daher, dass ein diskreter Grauwert auch nur auf einen anderen diskreten Grauwert abgebildet und nicht „auseinandergezogen“ werden kann. Tritt ein Grauwert sehr häufig auf, so werden seine direkten „Nachbarn“ auf der Grauwertskala nach der Gleichverteilung im Bild nicht mehr vorkommen.

Als Basis zur Ermittlung der Transformationskennlinie dient das sogenannte kumulative Grauwerthistogramm $H_{k}$ des Bildes. Dieses wird berechnet, indem jedem Grauwert g die Summe aller relativen Häufigkeiten H der Grauwerte 0 bis g zugeordnet wird:

H_{k}(g)=\sum _{n=0}^{g}H(n)

Dieses kumulative Grauwerthistogramm stellt eine Folge von Werten im Intervall $\lbrack 0,1\rbrack$ dar. Durch Multiplikation jedes Folgengliedes mit G und anschließender Rundung ergibt sich die Transformationskennlinie mit Wertebereich $\lbrace 0,\ldots ,G\rbrace$ :

T_{\text{equal}}(g)=\left\lbrack G\cdot H_{k}(g)\right\rbrack

Die Histogrammäqualisation ist verlustbehaftet, da größere Bereiche der Skala mit Grauwerten geringer Häufigkeit auf wenige Grauwerte komprimiert werden. Daher ist sie nicht umkehrbar.

Beispielbild: Kleiner Krater auf dem Mars (Aufnahme des Opportunity-Rovers)	(a) Bild nach Histogrammäqualisation	(b) Bild nach Histogrammhyperbolisation mit α = -1/3
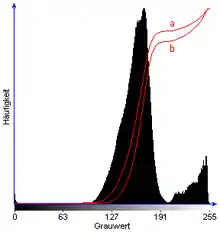Histogramm mit Transformationskennlinien	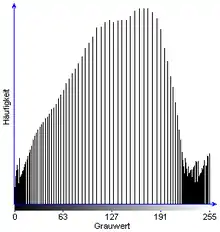Histogramm	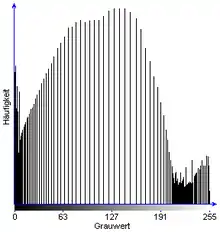Histogramm

Histogrammhyperbolisation

Nach einer Histogrammäqualisation sind die Grauwerte im Ergebnisbild zwar gleichverteilt, für einen menschlichen Betrachter wirkt dieses aber oft zu hell. Das liegt daran, dass die Helligkeitsempfindung unseres visuellen Systems nicht linear, sondern logarithmisch ist. Durch eine Histogrammhyperbolisation anstelle einer -äqualisation werden die Grauwerte dem subjektiven menschlichen Empfinden angepasst:

T_{\text{hyper}}(g)=\left\lbrack G\cdot H_{k}(g)^{\frac {1}{\alpha +1}}\right\rbrack

Die Transformationskennlinie der Gleichverteilung wird so etwas in Richtung eines hyperbolischen Verlaufs verschoben. Die dunklen Grauwerte erhalten eine höhere Wahrscheinlichkeit als die hellen, das Bild wird dadurch insgesamt abgedunkelt. $\alpha$ kann Werte aus dem Intervall $\rbrack -1,0\rbrack$ annehmen. Üblich sind Werte von $\alpha =-2/3$ bis $\alpha =-1/3$ , für $\alpha =0$ entspricht die Hyperbolisation der Äqualisation. Wird auf den Grauwert 0 verzichtet, so kann mit $\alpha \rightarrow -1$ eine logarithmische Wahrscheinlichkeitsverteilung der Grauwerte erreicht werden.

Da die Histogrammhyperbolisation auf der nicht umkehrbaren Histogrammäqualisation basiert und ähnlich verlustbehaftet ist, ist sie ebenfalls nicht umkehrbar.

Globale Schwellwertverfahren

Globale Schwellwertverfahren kommen häufig im Bereich der Bildsegmentierung zum Einsatz. Dabei wird jedes Pixel eines Grauwertbildes auf Grundlage seines Grauwertes einer von zwei Klassen zugeordnet. Auf diese Art und Weise wird beispielsweise oft der Bildvordergrund vom Hintergrund getrennt oder zwischen unterschiedlich hellen Objekten unterschieden. Die Grenze zwischen den beiden Klassen wird durch einen Schwellwert t festgelegt:

T_{\text{thresh}}(g)={\begin{cases}0&{\text{falls }}g<t\\1&{\text{falls }}g\geq t\end{cases}}

Die Anwendung des Schwellwerts führt zu einer Binarisierung des Bildes, d. h. das Ergebnisbild enthält nur noch die Werte 0 und 1. Soll die Farbtiefe des Bildes erhalten bleiben, so können die Grauwerte alternativ auf 0 (schwarz) und den größten möglichen Grauwert G (weiß) abgebildet werden:

T_{\text{thresh}}(g)={\begin{cases}0&{\text{falls }}g<t\\G&{\text{falls }}g\geq t\end{cases}}

Eine solche Trennung kann jedoch nur optimal funktionieren, wenn ein bimodales Histogramm wie im Beispiel unten vorliegt, wenn also zwei lokale Maxima im Histogramm existieren. Zur Wahl eines optimalen Schwellwerts gibt es verschiedene Ansätze, am bekanntesten unter den nicht-trivialen ist wohl das Otsu-Verfahren.

Neben den globalen gibt es auch lokale Schwellwertverfahren. Diese sind jedoch keine Punktoperatoren, denn bei ihnen werden die Schwellwerte auf Basis einer kleinen Bildregion oder einer Nachbarschaft individuell für jede Region bzw. jedes Pixel individuell festgelegt.

Weiterführende Informationen zu diesem Thema finden sich im Artikel Schwellwertverfahren.

Beispielbild

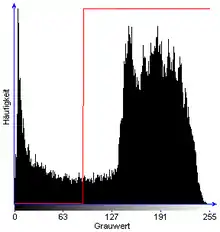Histogramm mit Transformationskennlinie

Bild nach Segmentierung mit Schwellwert 90

Pseudokolorierung

Wärmebild eines Hundes

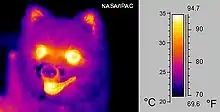
Die Pseudokolorierung ist ein Verfahren zur Einfärbung von Intensitätsbildern, etwa Wärmebildaufnahmen, um geringe Helligkeitsunterschiede innerhalb eines Bildes besser sichtbar zu machen. Das geschieht durch eine Abbildung des Definitionsbereichs der Intensitätswerte (die als Grauwerte aufgefasst werden können) auf eine kontrastreichere Farbskala. Jedem Intensitätswert g wird dabei ein Vektor ${\vec {g^{*}}}$ zugeordnet:

{\vec {g^{*}}}=(r^{*},g^{*},b^{*})^{T}=T(g)

Die Zusammensetzung des Vektors ${\vec {g^{*}}}$ ist durch den verwendeten Farbraum bestimmt. In diesem Fall stehen die drei Komponenten r*, g* und b* für den roten, grünen und blauen Farbanteil im RGB-Farbraum.

Ein Problem, das bei diesem Verfahren berücksichtigt werden muss, ist die unterschiedliche Helligkeitswahrnehmung des menschlichen visuellen Systems für verschiedene Farben. Der Mensch nimmt beispielsweise eine gelbe Fläche wesentlich heller als eine blaue Fläche gleicher Intensität wahr. Deshalb ist die Auswahl und Abfolge der einzelnen Farben für die Farbskala nicht willkürlich. Subjektiv „dunkle Farben“, wie beispielsweise blau oder violett, werden am unteren Ende der Skala benutzt, wogegen die „hellen Farben“ ans obere Ende der Skala gesetzt werden. Das ist sehr schön am nebenstehenden Beispiel zu sehen, wo rechts neben dem eingefärbten Wärmebild eines Hundes die benutzte Farbskala dargestellt ist. Da die Abfolge der einzelnen Farbwerte nicht trivial ist, kann sie oft nicht durch eine einfache Funktion beschrieben werden. Daher wird bei diesem Verfahren gewöhnlich eine Lookup-Tabelle eingesetzt, die in diesem speziellen Fall auch Color-Map genannt wird.

Es ist ebenfalls möglich, die Farbwerte eines Farbbildes auf eine andere Farbskala abzubilden. Diese sogenannte Falschfarbendarstellung funktioniert ähnlich wie die Pseudokolorierung, nur mit dem Unterschied, dass jedem Farbkomponenten-Vektor ${\vec {g}}$ ein anderer Vektor ${\vec {g^{*}}}$ zugeordnet wird:

{\vec {g^{*}}}=(r^{*},g^{*},b^{*})^{T}=T({\vec {g}})=T((r,g,b)^{T})

Inhomogene Standardtransformationen

Inhomogene Punktoperatoren werden im Allgemeinen wesentlich seltener benutzt als die homogenen Operatoren. Das liegt zum einen daran, dass die Anwendungsfälle einfach nicht so häufig gegeben sind, und zum anderen daran, dass die Implementierung vieler Verfahren nicht-trivial ist. Im Folgenden sollen zwei ausgewählte einfache inhomogene Transformationen vorgestellt werden.

Korrektur inhomogener Beleuchtung

Bei wissenschaftlichen Versuchsreihen, deren Versuchsaufbau Bildaufnahmen einschließt, beispielsweise Aufnahmen von Zellkulturen oder Mikroskopiebilder von Zellen in Flüssigkeit, können verschiedene Störeffekte auftreten, die die Weiterverarbeitung der Bilder manchmal erheblich stören. So ist trotz eines hohen Aufwands für den Versuchsaufbau und größter Sorgfalt immer eine (wenn auch oft nur minimal) ungleichmäßige Beleuchtung der Szene gegeben. Eine weitere Störquelle sind kleine Staubpartikel auf einer Linse oder auf dem Glas vor dem CCD-Sensor. Diese werden zwar nur sehr unscharf aufgenommen, da der Fokus der Kamera in einem anderen Bereich liegt, und sind im Bild nicht direkt sichtbar, absorbieren aber Licht und reduzieren die Helligkeit in einem Teil des Bildes. Ein weiteres Problem bei Geräten mit digitaler Aufnahmetechnik, insbesondere wenn preiswerte CMOS-Sensoren zum Einsatz kommen, ist eine ungleichmäßige Sensitivität der einzelnen Fotorezeptoren.

Alle diese Effekte erschweren die Bildanalyse, insbesondere die Segmentierung von Objekten und Hintergrund. Das kann so weit reichen, dass der Hintergrund an einigen Stellen dunkler ist als die Objekte und eine Segmentierung mit einem globalen Schwellwert gänzlich unmöglich wird. Wurde jedoch vor oder nach dem Versuch ein Referenzbild aufgenommen, also ein Bild der ungleichmäßig beleuchteten Szene unter Versuchsbedingungen, aber ohne Objekte, so können die oben beschriebenen Störeffekte eliminiert werden und das Ergebnisbild $f^{*}$ hat im Idealfall einen weißen Hintergrund mit homogener Helligkeit. Berechnet wird es durch punktweise Division des Versuchsbildes f durch das Referenzbild $f_{r}$ und anschließende Normierung auf den gewünschten Wertebereich $\lbrace 0,\ldots ,G\rbrace$ :

f^{*}(x,y)=T_{xy}(f(x,y))=\left\lbrack G\cdot {\frac {f(x,y)}{f_{r}(x,y)}}\right\rbrack

Dieses Verfahren ist unter Umständen selbst dann noch anwendbar, wenn zu einer Versuchsreihe kein Referenzbild existiert. Denn wenn die aufgenommenen Objekte klein und zufällig in den Bildern verteilt sind, so gibt es die Möglichkeit, ein Mittelwertbild aus mehreren oder allen Bildern der Reihe als Referenzbild zu benutzen.

Objekte vor einem ungleichmäßig beleuchteten Hintergrund

Ungleichmäßig beleuchteter Hintergrund

Ungleichmäßige Beleuchtung korrigiert

Fensterfunktion

Für die Berechnung der Fouriertransformation eines Bildes wird dieses als periodisch angenommen. Ist jedoch eine mögliche Periodizität nicht gegeben, weisen also der linke und der rechte bzw. der obere und der untere Bildrand verschiedene Helligkeiten oder Strukturen auf, so führt eine periodische Wiederholung zu Unstetigkeiten an den Bildrändern. Diese sind im Spektrum als hohe spektrale Dichten entlang der Achsen sichtbar (siehe Beispiel unten). Bei der Anwendung weiterführender Operationen im Fourierraum, beispielsweise einer Faltung mit einem Glättungsoperator, können diese hohen Dichten erheblich stören.

Der Störeffekt kann durch Multiplikation des Bildes f mit einer geeigneten Fensterfunktion w, die Werte im Intervall $\lbrack 0,1\rbrack$ annimmt und von der Mitte zum Bildrand hin auf 0 abfällt, vermieden werden:

f^{*}(x,y)=w(x,y)\cdot f(x,y)

Bei der beispielhaften Verwendung eines Kosinusfensters (wie im Beispiel unten) ergibt sich folgende Transformationsvorschrift, wobei X und Y die Anzahl der Pixel in x- bzw. y-Richtung darstellen:

f^{*}(x,y)=\sin {\left(\pi \cdot {\frac {x}{X}}\right)}\cdot \sin {\left(\pi \cdot {\frac {y}{Y}}\right)}\cdot f(x,y)\qquad {\text{mit }}0\leq x<X,0\leq y<Y

Natürlich ändert sich durch die Fensterung des Bildes auch das gesamte Spektrum geringfügig.

Beispielbild
Fourierspektrum des Bildes (hohe spektrale Dichten entlang der Achsen)
Fensterung des Beispielbildes
Fourierspektrum des gefensterten Bildes

Referenzen

Literatur

Thomas Lehmann, Walter Oberschelp, Erich Pelikan, Rudolf Repges: Bildverarbeitung für die Medizin: Grundlagen, Modelle, Methoden, Anwendungen. Springer-Verlag, Berlin 1997, ISBN 3-540-61458-3
Bernd Jähne: Digitale Bildverarbeitung. 6., überarbeitete und erweiterte Auflage. Springer-Verlag, Berlin 2005, ISBN 3-540-24999-0
Rafael C. Gonzalez, Richard E. Woods: Digital Image Processing. 2. Auflage, Prentice Hall, 2001, ISBN 0-20-118075-8 (englisch)

Weblinks

Bildverarbeitung für die Medizin von Thomas Lehmann u. a. als Download-Version (PDF 6,2 MB)
Bildverarbeitung in der Praxis von Rainer Steinbrecher in der 2. überarbeiteten Auflage als Download-Version (PDF 6,1 MB) (1. Auflage: ISBN 3-486-22372-0)

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.