Kennlinie
Eine Kennlinie ist die graphische Darstellung des Zusammenhangs zwischen zwei physikalischen Größen, der für ein Bauelement, eine Baugruppe oder ein Gerät kennzeichnend ist. Der Zusammenhang wird als Linie in einem ebenen Koordinatensystem angegeben. Die Kennlinie dient zur Veranschaulichung des Zusammenhangs, aber auch zu dessen quantitativer Wiedergabe, wenn eine algebraische Funktion des Zusammenhangs nicht bekannt ist. Während eine Kennlinie direkt aus Messwerten gewonnen werden kann, kann eine theoretisch nicht untermauerte, gleichwohl näherungsweise richtige Funktion z. B. aus Messwerten durch Interpolation und Regression ermittelt werden.
Soll eine weitere Eingangsgröße (Parameter) beachtet werden, so zeichnet man mehrere Kennlinien zu einzelnen Werten des Parameters
- in einem Kennlinienfeld oder kurz Kennfeld mit gemeinsamem Koordinatensystem oder
- in einer Parallelprojektion, in welcher der Parameter wie eine Variable eine eigene Achse erhält.
-Kennlinie.svg.png.webp)
waagerecht: ideal; geneigt: real linear;
gekrümmt: real nichtlinear, hier: Solarzelle. Die drei Geraden bilden ein Kennlinienfeld mit dem Quellwiderstand als Parameter.
Beispiele
Einfach sind lineare Zusammenhänge darstellbar, wie in den Grundlagen der Elektrotechnik: Der Zusammenhang zwischen elektrischer Spannung und elektrischer Stromstärke bei einem linearen Widerstand in Form einer geneigten, durch den Koordinatenursprung gehenden Geraden – oder der Zusammenhang zwischen und bei einer idealen Spannungsquelle in Form einer waagerechten Geraden. Lineare Darstellungen sind häufig Idealisierungen, und die realen Zusammenhänge sind nichtlinear. Dann sind Kennlinien besonders wichtig.
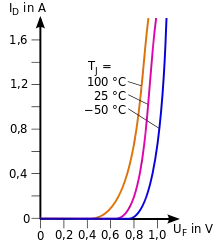
Der Zusammenhang zwischen und bei einer Diode hat einen näherungsweise exponentiell ansteigenden Verlauf. Wird die Temperatur der Diode als Parameter hinzugenommen, wird daraus ein Kennlinienfeld mit mehreren Strom-Spannungs-Kennlinien zu ausgewählten Temperaturen.
Manche elektrische Bauelemente sind mechanisch veränderbar durch Drehen oder Verschieben. Insbesondere Widerstände sind als Stellwiderstände und Potentiometer verfügbar. Die Kennlinie beschreibt hier den Widerstandswert in Abhängigkeit von der Position (Drehwinkel) eines Schleifers. Neben der linearen Kennlinie mit gibt es auch die positiv-logarithmische (ausgehend von ändert sich der Widerstand anfangs nur wenig) und die negativ-logarithmische (ausgehend von ändert sich der Widerstand anfangs sehr stark).[1] Mit der positiv-logarithmischen Kennlinie (angestrebter Zusammenhang ) eines Lautstärke-Potentiometers ergibt sich eine dem menschliche Ohr angepasste Einstellempfindlichkeit.[2]
In der Regelungstechnik gibt es Kennlinien, die das statische Verhalten eines Systems beschreiben, und auch solche für ein einzelnes Bauteil. Beispielsweise für Stellventile gibt es neben linearen auch gleichprozentige Kennlinien, deren Krümmung der Krümmung der nichtlinearen Kennlinie der Regelstrecke entgegengesetzt ist.[3] „Gleichprozentig“ bedeutet hier, dass zu gleichen Hubänderungen gleiche relative Durchflussänderungen gehören (prozentual bezogen auf den aktuellen Durchfluss).[4][5]
In der Digitaltechnik werden Quantisierungskennlinien mit treppenförmigem Verlauf verwendet. Neben der linearen Quantisierungskennlinie mit über den gesamten Darstellungsbereich gleich breiter Stufung gibt es auch nichtlineare Kennlinien mit innerhalb ihres Wertebereiches feinerer Stufung bei kleineren Signalen.
Alternativen
Als Alternativen zur Kennlinie werden beispielhaft genannt:
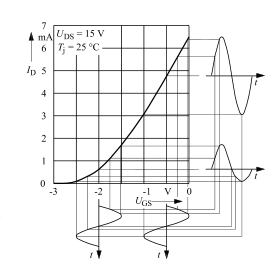
Ausschnittvergrößerung: Häufig ergibt sich für Bauelemente mit nichtlinearer Kennlinie durch eine kleine Aussteuerung um einen Arbeitspunkt herum näherungsweise ein linearer Zusammenhang zwischen der Eingangs- und der Ausgangsgröße, wozu sich für das Kleinsignalverhalten eine lineare Kennlinie anwenden lässt.
Tabelle: In elektronischen Steuerungen und Mikrocontrollern sind Kennlinien oder -felder als Tabellenwerte oder als analytische Funktionen gespeichert, um komplexe Prozesse zu steuern. Eine Anwendung ist die Kennfeldsteuerung von Verbrennungsmotoren, wozu das Motorkennfeld diskretisiert wird.[6] Zwischen den Tabellenwerten wird meist linear interpoliert.
Funktion: Die Spannungs-Temperatur-Kennlinien für Thermoelemente werden in der Normung durch Funktionen angegeben. Diese sind für Anwendungen ohne Rechner-Unterstützung jedoch so mühsam handhabbar, dass zusätzlich Tabellen bereitgestellt werden.
Parallelprojektion
.de.svg.png.webp)
Als Beispiel für eine Parallelprojektion zeigt nebenstehendes Diagramm für Wasser den Zusammenhang zwischen Druck , spezifischem Volumen und Temperatur . Zu mehreren festgehaltenen Werten des Parameters sind -Kennlinien eingetragen für den Zusammenhang zwischen und .
Ein ausführlicheres Diagramm (und ohne die Anomalie des Wassers) findet sich in[7], in dem auch -Kennlinien bei konstantem als Parameter enthalten sind.
Siehe auch
Einzelnachweise
- Wolfgang Oberthür: Basiswissen Elektrotechnik/Elektronik für nicht elektrotechnische Berufe. Books on Demand, 8. Aufl. 2010, S. 22
- Erwin Böhmer, Dietmar Ehrhardt, Wolfgang Oberschelp: Elemente der angewandten Elektronik: Kompendium für Ausbildung und Beruf. Vieweg + Teubner, 16. Aufl. 2010, S. 10–11
- Ernst-Rudolf Schramek, Hermann Recknagel (Hrsg.): Taschenbuch für Heizung und Klimatechnik einschließlich Warmwasser- und Kältetechnik. Oldenbourg, 73. Aufl. 2007, S. 327
- Günther Strohrmann: Automatisierung verfahrenstechnischer Prozesse: eine Einführung für Techniker und Ingenieure. Oldenbourg, 2002, S. 277
- Hans Roos: Hydraulik der Wasserheizung. Oldenbourg, 5. Aufl. 2002, S. 65
- Wolf-Heinrich Hucho: Sindbad: von einem, der auszog, das Fürchten zu lernen. Selbstverlag, 2017
- Zustandsgebiet im p-v-T-Diagramm (Memento vom 21. Januar 2016 im Internet Archive) (abgerufen am 3. April 2018)