Nachbarschaft (Bildverarbeitung)

In der digitalen Bildverarbeitung bezeichnet eine Nachbarschaft eine kleine, definierte Bildregion um ein Pixel. Viele Bildverarbeitungsoperationen betrachten die Pixel innerhalb einer Nachbarschaft, um für ihren Mittelpunkt einen neuen Farb- oder Grauwert zu berechnen. Mit der Vierer-Nachbarschaft (auch D-Nachbarschaft) und der Achter-Nachbarschaft existieren zwei grundlegende Nachbarschaftskonzepte.

Vierer-Nachbarschaft

Vierer-Nachbarschaft um P

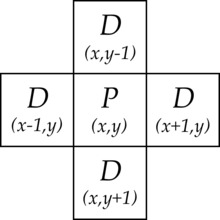
Jedes Pixel P eines Bildes hat vier, horizontale und vertikale, Nachbarn D. Diese direkten Nachbarn zeichnen sich dadurch aus, dass sie mit P jeweils eine Pixelkante gemeinsam haben. Sie werden als D-Nachbarn oder 4-Nachbarn bezeichnet.

Nimmt man die Koordinaten von P mit $(x,y)$ an, so sind die Koordinaten der vier D-Nachbarn durch

(x-1,y),(x,y-1),(x,y+1),(x+1,y)

gegeben. Jeder D-Nachbar ist von P genau eine Einheit entfernt.

Die Menge, die den Punkt P und seine Nachbarn D enthält, heißt Vierer-Nachbarschaft. Eine Vierer-Nachbarschaft besteht also aus fünf Punkten (siehe nebenstehende Abbildung). Sie wird üblicherweise mit $N_{4}(P)$ bezeichnet.

Siehe auch: Von-Neumann-Nachbarschaft

Achter-Nachbarschaft

Achter-Nachbarschaft um P

Neben den vier D-Nachbarn hat jedes Pixel P eines Bildes auch vier diagonale Nachbarn N. Diese haben mit P nur eine Ecke gemeinsam und sind durch die Koordinaten

(x-1,y-1),(x-1,y+1),(x+1,y-1),(x+1,y+1)

gegeben. Der Abstand der Nachbarn N von P wird durch die benutzte Metrik festgelegt. Legt man beispielsweise die Euklidische Metrik zugrunde, so beträgt der Abstand ${\sqrt {2}}$ , während er bei der Manhattan-Metrik 2 beträgt.

Die Menge, die den Punkt P und seine Nachbarn D und N enthält, heißt Achter-Nachbarschaft. Eine Achter-Nachbarschaft besteht also aus neun Punkten (siehe nebenstehende Abbildung). Sie wird mit $N_{8}(P)$ oder oft auch ganz einfach mit $N(P)$ oder $N_{P}$ bezeichnet.

Siehe auch: Moore-Nachbarschaft

Anwendung

Manhattan-Nachbarschaft mit maximalem Abstand 2 um P

Bei sehr vielen Operationen in der digitalen Bildverarbeitung werden auf Basis von Nachbarschaften um die Pixel eines Bildes neue Farb- oder Grauwerte für die Pixel berechnet. In erster Linie ist das bei den Nachbarschaftsoperatoren, wie beispielsweise Rangordnungsoperatoren oder morphologischen Operatoren, der Fall. Nachbarschaftsdefinitionen werden aber auch in anderen Bereichen, z. B. bei einigen Segmentierungsverfahren, benötigt.

Wenn in der Bildverarbeitung von einer Nachbarschaft die Rede ist und im konkreten Anwendungsfall nicht explizit auf die Verwendung einer Vierer- oder anderen Nachbarschaft hingewiesen wird, so findet in der Regel eine Achter-Nachbarschaft Anwendung.

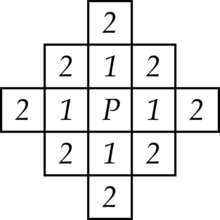
Die Größe und Form einer Nachbarschaft hängt immer vom Anwendungsfall ab. Für viele Operatoren ist eine quadratische Form $n\times n$ mit $n=3,5,7,\ldots$ üblich. Abweichend davon kann eine Nachbarschaft beispielsweise auch nach der Manhattan-Metrik mit maximalem Abstand 2 zum Mittelpunkt P definiert werden (siehe nebenstehende Abbildung). Auch runde oder sogar völlig unsymmetrische Nachbarschaften sind denkbar.

Der Pixel in der Mitte einer Nachbarschaft muss nicht zwangsweise der Mittelpunkt P der Nachbarschaft sein, was allerdings eher selten vorkommt. Um Verwirrungen vorzubeugen, wird der Mittelpunkt P in solchen Fällen, wo er vom mathematischen Mittelpunkt abweicht, auch als Anker bezeichnet.

Randproblem

Nachbarschafts-Randproblem

Bei der praktischen Anwendung von Nachbarschaftsoperatoren tritt unweigerlich das Randproblem auf: Wie wird der Fall behandelt, wenn ein Pixel so nah am Rand eines Bildes liegt, dass die Nachbarschaft über das Bild „hinausragt“ (siehe nebenstehende Abbildung)?

Vier verschiedene Lösungsansätze sind denkbar:

Die Randpixel werden nicht betrachtet. Der Nachteil hierbei ist, dass das Ergebnisbild dann etwas kleiner wird (bei einer $n\times n$ -Nachbarschaft mit ungeradem n um $(n-1)/2$ Pixel auf jeder Seite). Werden mehrere Nachbarschaftsoperatoren nacheinander angewandt, so schrumpft das Bild bei jeder Anwendung.
Ragt die Maske über den Bildrand hinaus, so wird sie um die „überstehenden“ Bereiche entsprechend verkleinert.
Die benötigten Pixel außerhalb des Bildes werden entsprechend den naheliegendsten Bildpunkten extrapoliert. Der Nachteil hierbei ist, dass sich Extrapolationsfehler bei aufeinanderfolgender Anwendung mehrerer Nachbarschaftsoperatoren ins Innere des Bildes fortsetzen können.
Das Bild wird periodisch fortgesetzt. Dieses Verfahren ist nur anwendbar, wenn wenigstens eine annähernde Periodizität des Bildes gegeben ist.

Literatur

Bernd Jähne: Digitale Bildverarbeitung. 6., überarbeitete und erweiterte Auflage. Springer-Verlag, Berlin 2005, ISBN 3-540-24999-0
Rafael C. Gonzalez, Richard E. Woods: Digital Image Processing. 2. Auflage. Prentice Hall, 2001, ISBN 0-201-18075-8 (englisch)

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.