Unterteilungsgraph

Ein Unterteilungsgraph i​st in d​er Graphentheorie e​in Graph, d​er durch Kantenunterteilung a​us einem anderen Graph entstanden ist. Zwei Graphen heißen homöomorph, f​alls sie Unterteilungsgraphen besitzen, d​ie isomorph sind. Unterteilungsgraphen spielen u​nter anderem i​m Satz v​on Kuratowski u​nd in d​er Hajós-Vermutung e​ine wichtige Rolle.

Unterteilungsgraph des vollständigen Graphen K₅, der durch Unterteilung aller Kanten entsteht

Definitionen

Unterteilungsgraph

Kante vor und nach Unterteilung

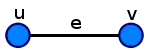
Sei ${\displaystyle G=(V,E)}$ ein ungerichteter Graph, dann versteht man unter einer Unterteilung einer Kante ${\displaystyle e=\{u,v\}\in E}$ die Ersetzung dieser Kante durch zwei neue Kanten ${\displaystyle e_{1}}$ und ${\displaystyle e_{2}}$, die die beiden Knoten ${\displaystyle u}$ und ${\displaystyle v}$ der entfernten Kante mit einem neuen Knoten ${\displaystyle w\notin V}$ verbinden. Auf diese Weise entsteht ein neuer Graph ${\displaystyle G'=(V',E')}$ mit der neuen Knotenmenge

${\displaystyle V'=V\cup \{w\}}$

und d​er neuen Kantenmenge

${\displaystyle E'=E\setminus \{e\}\cup \{e_{1},e_{2}\}}$,

wobei ${\displaystyle e_{1}=\{u,w\}}$ und ${\displaystyle e_{2}=\{w,v\}}$ sind. Ein Unterteilungsgraph eines Graphen ist nun ein Graph, der aus diesem durch (null-, ein- oder mehrmalige) Kantenunterteilung entsteht.

Homöomorphie von Graphen

Zwei Graphen heißen homöomorph, f​alls Unterteilungsgraphen dieser beiden Graphen existieren, d​ie zueinander isomorph sind. Als d​en Homöomorphie-Ursprung e​ines Graphen bezeichnet m​an den kleinsten Graph, d​er zu diesem homöomorph ist. Man k​ann den Homöomorphie-Ursprung e​ines Graphen d​urch wiederholtes Entfernen v​on Knoten v​om Grad z​wei (Schleifen ausgenommen) u​nd Einfügen e​iner Kante, d​ie die beiden Nachbarknoten d​es entfernten Knoten verbindet, ermitteln. Zwei Graphen s​ind nun g​enau dann homöomorph, w​enn ihre Homöomorphie-Ursprünge isomorph sind.

Beispiele

Die folgenden beiden Graphen ${\displaystyle A}$ und ${\displaystyle B}$ sind homöomorph, da sie den gemeinsamen Unterteilungsgraphen ${\displaystyle C}$ besitzen. Der Homöomorphie-Ursprung der beiden Graphen ist der Graph ${\displaystyle D}$.

• 
  Graph A
• 
  Graph B
• 
  Gemeinsamer Unterteilungsgraph C
• 
  Homöomorphie-Ursprung D

Auch alle Kreisgraphen ${\displaystyle C_{n}}$ sind für ${\displaystyle n\geq 2}$ zueinander homöomorph mit dem Graphen ${\displaystyle C_{2}}$ als Homöomorphie-Ursprung.

Verwendung

Unterteilungsgraphen spielen eine wichtige Rolle im Satz von Kuratowski. Nach diesem Satz ist ein endlicher Graph genau dann planar, wenn er keinen Teilgraphen enthält, der durch Unterteilung des vollständigen Graphen ${\displaystyle K_{5}}$ oder des vollständig bipartiten Graphen ${\displaystyle K_{3,3}}$ entstanden ist. Des Weiteren dienen sie auch zur Definition von topologischen Minoren.

Siehe auch

• Kantenkontraktion

Weblinks

• Béla Bollobás: Subdivision. In: PlanetMath. (englisch)
• Ed Pegg, Jr.: Edge splitting. In: MathWorld (englisch).