Periodische Randbedingung

Periodische Randbedingungen werden in analytischen oder numerischen Modellrechnungen gewählt, um eine gesonderte Behandlung von Rändern zu vermeiden oder das Gebiet, über das sich die Rechnung erstreckt, verkleinern zu können. Periodische Randbedingungen in $d$ Dimensionen können als Kompaktifizierung des Raumes zu einem flachen Torus in $d+1$ Dimensionen aufgefasst werden.[1]

Anwendungsgebiete sind die Festkörperphysik kristalliner Materialien, Molekulardynamik, Monte-Carlo-Simulationen sowie Simulationen auf Gittern wie Gittereichtheorien.

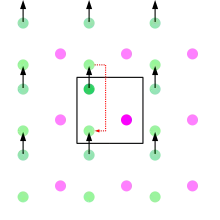
Periodische Randbedingungen in zwei Dimensionen. Der Rand der Simulationsbox ist schwarz dargestellt.

Bei kontinuierlichen Teilchensimulationen mit periodischen Randbedingungen treten Teilchen an einem Rand der Simulationsbox (dem Simulationsgebiet) aus und am gegenüberliegenden Rand wieder ein.

Mathematische Definition

Eine partielle Differentialgleichung ist eine Gleichung, in der Ableitungen einer unbekannten Funktion

u\colon \Omega \to \mathbb {R}

für eine offene Teilmenge $\Omega \subset \mathbb {R} ^{d},d\geq 2$ vorkommen. Man spricht von periodischen Randbedingungen, wenn $\Omega$ von der Form

\Omega =(a_{1},b_{1})\times \ldots \times (a_{d},b_{d})\subset \mathbb {R} ^{d}

ist und man verlangt, dass es eine stetige Fortsetzung $u\colon {\overline {\Omega }}\to \mathbb {R}$ mit

u(x_{1},\ldots ,x_{i-1},a_{i},x_{i+1},\ldots ,x_{d})=u(x_{1},\ldots ,x_{i-1},b_{i},x_{i+1},\ldots ,x_{d})\ \forall (x_{1},\ldots ,x_{d})\in \Omega ,i=1,\ldots ,d

geben soll.[2]

$\Omega$ muss nicht quaderförmig sein, aber eine vollständige periodische Abdeckung des Raumes erlauben[3] (siehe Raumfüllung und Parkettierung).

Kompaktifizierung

Eine rechteckige Fläche wird zu einem Torus zusammengelegt; ihre Ränder verschwinden.
Die für die 3D-Ansicht nötige Verzerrung tritt in der Anwendung nicht auf.

Periodische Randbedingungen in allen $d$ Dimensionen entsprechen einem flachen Torus in $d+1$ Dimensionen, d. h. mit nicht gekrümmter Oberfläche. Die Oberfläche ist deshalb nicht als Teilmenge des $d+1$ -dimensionalen Raumes beschreibbar, sondern als kartesisches Produkt von $d$ Kreisen.

Erhaltungsgrößen

Periodische Randbedingungen erlauben Energie- und Impulserhaltung, verletzen aber die Drehimpulserhaltung.[4] Formal: Drehimpulserhaltung ist Folge der hier nicht gegebenen Invarianz der physikalischen Gesetze gegenüber Drehungen des Bezugssystems. Anschaulich: Ein lokal gestarteter Wirbel wächst durch Impulsdiffusion bis auf die Längenskala der Simulationsbox an und wird dann systematisch vernichtet.

Beispiele

Periodische Lösung für ein periodisches Problem

Im ersten Beispiel werden periodische Randbedingungen mit verschiedenen nichtperiodischen Randbedingungen kombiniert. Es geht um die Simulation der Umströmung von Turbinenschaufeln in einem Ringspalt. Es gelte die Annahme (oder Näherung), dass die Umströmung aller N Schaufeln gleich sei. Das Problem hat damit eine N-zählige Drehsymmetrie, die ausgenutzt werden soll, indem als Simulationsgebiet ein Sektor gewählt wird, der lediglich eine der Schaufeln enthält. Am Ende soll die für den Sektor gefundene Lösung N-fach vervielfältigt zum Ring zusammengesetzt werden. Der Rechenaufwand beschränkt sich damit auf einen Bruchteil des Gesamtgebiets, und die Gesamtlösung hat automatisch die erwartete Symmetrie, d. h. sie ist periodisch.

Damit die Lösung aber physikalisch sinnvoll sein kann, muss sie an den Nahtstellen so glatt zusammenpassen, wie es von der Lösung auch im Inneren des Simulationsgebiets verlangt wird. Diese Forderung macht die periodischen Randbedingungen aus. Zudem muss in diesem speziellen Beispiel die Lösung an den festen Innen- und Außenflächen entsprechende Randbedingungen erfüllen (z. B. Strömungsgeschwindigkeit = Wandgeschwindigkeit, falls die Grenzschicht im Detail modelliert wird) und stromauf- und -abwärts mit den Lösungen für weitere Turbinenstufen passen (es gilt, eine gemeinsame Lösung zu finden).

Wie man zu Lösungen kommt, die die periodischen Randbedingungen erfüllen, hängt davon ab, wie überhaupt die physikalischen Größen des Problems (hier Druck, Temperatur und Geschwindigkeitskomponenten) repräsentiert werden sollen. Eine Möglichkeit wäre, als Summe von Basisfunktionen, die einzeln jeweils periodisch und glatt sind, also z. B. sinusförmig vom Winkel um die Drehachse abhängen, siehe Fourier-Reihe. Ein Rand tritt dann nicht auf. Eine andere hier geeignetere Klasse von Verfahren nutzt zahlreiche Stützstellen (Gitterpunkte), siehe z. B. Finite-Volumen-Verfahren. Dabei werden Gitterpunkte an einer Seite des Simulationsgebiets mit solchen auf der anderen Seite als benachbart definiert, um der Randbedingung Genüge zu tun.

Ignorieren von Oberflächenwellen

In einem quaderförmigen Einkristall sind Phononen Anregungen mechanischer stehender Wellen. Ignoriert man, dass die Atome in Randlage abweichende Nachbarschaftsverhältnisse haben, so vereinfacht sich die Wellengleichung auf die für das unendlich ausgedehnte Gitter. Die Lösungen sind Überlagerungen ebener Wellen der Art

u(x,y,t)=u_{0}\cdot e^{\mathrm {i} (k_{x}\cdot x+k_{y}\cdot y-\omega \cdot t)}

Darin sind

die Komponenten von $u$ die der Auslenkungen aller Atome der kristallographischen Elementarzelle aus ihren Ruhelagen
$x$ und $y$ Ortskoordinaten (der Einfachheit halber in nur zwei Dimensionen)
$t$ die Zeit
$\omega$ die Frequenz, die abhängig ist vom Wellenvektor $k$ und von der im Amplitudenfaktor $u_{0}$ enthaltenen Polarisation.

Der einzige berücksichtigte Oberflächeneffekt ist die Beschränkung auf diskrete Wellenvektoren:

k_{x}={\frac {\pi \cdot n_{x}}{N_{x}\cdot a_{x}}}

k_{y}={\frac {\pi \cdot n_{y}}{N_{y}\cdot a_{y}}}

mit

natürlichen Zahlen $n$
der Größe $N$ des Kristalls in Einheiten der Größe $a$ seiner Elementarzelle.

Mit diesen $k$ erfüllen die Lösungen die Periodizitätsbedingung

u(x,y,t)=u(x+2\cdot N_{x}\cdot a_{x},y,t)=u(x,y+2\cdot N_{y}\cdot a_{y},t)

.

Im Born-von-Kármán-Modell werden periodische Randbedingungen auch Born-von Kármán-Randbedingungen genannt.[5]

Kompression ohne Schraubstock

Das Bild des Schraubstocks steht für große äußere Kräfte. Würde man simulierte Schraubstockbacken auf die Atome einer kleinen Simulationsbox einwirken lassen, wären die Ergebnisse unbrauchbar. Besonders große Kräfte sind nötig, um Materialien bei nicht im Labor realisierbaren Bedingungen, wie jenen im Erdkern, zu untersuchen (z. B. ihren Elastizitätstensor zu bestimmen). Durch die Verwendung periodischer Randbedingungen wird dieses Problem umgangen, indem nicht Kräfte (mechanische Spannungen) vorgegeben und Verformungen beobachtet werden, sondern umgekehrt. Die Simulationsbox enthält dazu eine einzige Elementarzelle des Kristalls und wird willkürlich verformt (Kantenlängen und Winkel). Für jede Geometrie der Elementarzelle wird die Lage der Atome variiert und jeweils die elektronische Energie berechnet (siehe Born-Oppenheimer-Näherung), wobei die Dichtefunktionaltheorie mit periodischen Basisfunktionen zum Einsatz kommt. Aus der Abhängigkeit der elektronischen Energie von der Geometrie der Elementarzelle bei relaxierter Anordnung der Atome ergeben sich die äußeren mechanischen Spannungen als Rechenergebnis.

Anwendungsgebiete mit nichtperiodischer Problemstellung

Der Vorteil der Wandlosigkeit durch periodische Randbedingungen lässt sich auch bei der Simulation von Systemen nutzen, die eigentlich nicht periodisch sind. Die Größe der Simulationsbox wird dann willkürlich, aber nicht beliebig gesetzt: sie muss größer sein als die Entfernungen, über die Korrelationen auftreten. Das kann ein großes Molekül in einer Lösung sein, eine Materialverformung oder eine Dichteschwankung nahe einem Phasenübergang.

Für kurzreichweitige Wechselwirkungen können Cutoff-Radien eingeführt werden, ab denen keine explizite Wechselwirkung zwischen Teilchen mehr berechnet wird, allerdings können weiterhin analytisch erhaltene Zusatzterme für die abgeschnittenen Wechselwirkungen berücksichtigt werden[6]. In dem Fall der Verwendung dieser Cutoff-Radien kann man ein Kriterium für eine nicht zu unterschreitende Größe der Simulationsbox angeben, wobei häufig noch andere Kriterien zu beachten sind, die deutlich größere Boxgröße erzwingen: Der kleinste Durchmesser der Simulationsbox sollte mindestens doppelt so groß sein wie der größte derartig verwendete Cutoff-Radius, ansonsten sieht ein Teilchen in der Simulationsbox (Central Box) eine Kopie seiner selbst in einer benachbarten Box. Weiterhin ist dies das Kriterium, damit man die Minimum Image Convention für diese Wechselwirkungen verwenden darf. Diese Konvention besagt, dass man nur Wechselwirkungen mit Teilchen in den nächsten benachbarten Boxen der Central Box beachten muss.

Thermodynamischer Limes und Kontinuumslimes

Um aus Molekulardynamik-Simulationen Aussagen zu thermodynamischen Größen zu erhalten, muss der thermodynamische Limes ermittelt werden, d. h. Teilchenzahl N und Volumen V müssen jeweils ins Unendliche gesteigert werden ( $N\to \infty ,V\to \infty$ ), bei konstanter Teilchenzahldichte $N/V$ . Dazu werden die Messgrößen für verschiedene Größen der Simulationsbox zu unendlicher Teilchenzahl und unendlichen Volumen interpoliert.

Man beachte, dass alleine die Anwendung periodische Randbedingungen nicht zum thermodynamischen Limes führt. Dies ist besonders deutlich, wenn man beispielsweise eine Flüssigkeit simulieren will, jedoch nur ein Flüssigkeitsteilchen in die Simulationsbox setzt. Betrachtet man die Simulationsbox sowie ihre Kopien, so wird man stets einen Kristall finden. Um die Flüssigkeit korrekt zu simulieren, müssen in der Hauptsimulationsbox bereits genug Teilchen vorliegen (N groß, geht in Richtung thermodynamischer Limes), sodass die interessanten Korrelationseffekte bereits hier auftreten und Finite-Size-Effekte (N klein) vernachlässigbar werden.

Periodische Randbedingungen dienen lediglich dazu, keine Randeffekte in die Simulation einzuführen und somit ein System ohne Ränder zu simulieren, wie es z. B. im Inneren (englisch Bulk) einer Flüssigkeit vorliegt.

Einzelnachweise

Hugo Reinhardt: Quantenmechanik 1: Pfadintegralformulierung und Operatorformalismus. ISBN 348671516X, S. 312 (Google Books).
Jürgen Jost: Partial differential equations (= Graduate Texts in Mathematics. 214) Third edition, Springer, New York 2013, ISBN 978-1-4614-4808-2.
Oleg Jardetzky, Michael D. Finucane (Hrsg.): Dynamics, Structure, and Function of Biological Macromolecules. IOS Press, 2001, ISBN 1586030329, S. 3 (Google Books).
On angular momentum balance for particle systems with periodic boundary conditions, https://arxiv.org/pdf/1312.7008.pdf
Mireille Defranceschi, Claude Le Bris: Mathematical Models and Methods for Ab Initio Quantum Chemistry. (= Lectures in Chemistry. 74), Springer, 2000 ISBN 3540676317, S. 96 (Google Books).
M. P. Allen, D. J. Tildesley: Computer Simulation of Liquids. Oxford University Press, 1989, ISBN 0-19-855645-4, S. 24 (eingeschränkte Vorschau in der Google-Buchsuche).

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Hugo Reinhardt: Quantenmechanik 1: Pfadintegralformulierung und Operatorformalismus. ISBN 348671516X, S. 312 (Google Books).

[2] Jürgen Jost: Partial differential equations (= Graduate Texts in Mathematics. 214) Third edition, Springer, New York 2013, ISBN 978-1-4614-4808-2.

[3] Oleg Jardetzky, Michael D. Finucane (Hrsg.): Dynamics, Structure, and Function of Biological Macromolecules. IOS Press, 2001, ISBN 1586030329, S. 3 (Google Books).

[4] On angular momentum balance for particle systems with periodic boundary conditions, https://arxiv.org/pdf/1312.7008.pdf

[5] Mireille Defranceschi, Claude Le Bris: Mathematical Models and Methods for Ab Initio Quantum Chemistry. (= Lectures in Chemistry. 74), Springer, 2000 ISBN 3540676317, S. 96 (Google Books).

[6] M. P. Allen, D. J. Tildesley: Computer Simulation of Liquids. Oxford University Press, 1989, ISBN 0-19-855645-4, S. 24 (eingeschränkte Vorschau in der Google-Buchsuche).