Pascals Barometer
Pascals Barometer ist ein Lehrstück der Lehrkunstdidaktik. Es wurde in den Jahren bis 1997 vom Berner Physikdidaktiker Ueli Aeschlimann[1] auf Basis eines Exempels von Martin Wagenschein aus den 1970er Jahren entwickelt und in den Jahren bis 2013 von Marc Eyer[2], inzwischen ebenfalls Professor an der PH Bern, neuinszeniert.
Das Lehrstück behandelt die Phänomene des Druckes unter Verwendung originärer Quellen und Vorlagen aus dem 17. Jahrhundert von Galileo Galilei, Gasparo Berti[3], Evangelista Torricelli, Blaise Pascal, Otto von Guericke und Robert Boyle. Es falsifiziert in genetischer Weise Aristoteles' Theorie des horror vacui.
Wagenscheins Exempel
.jpg.webp)
Martin Wagenschein war in den Jahren seit etwa 1971 häufig als Gastredner in pädagogischen Arbeitskreisen junger Schweizer Lehrkräfte aufgetreten. Zu jener Zeit gehörte ein spezielles Exempel zu seinem festen Repertoire: Er zog aus einer mit Wasser gefüllten Waschschüssel ein Bierglas mit der Öffnung nach unten heraus. Zum Erstaunen vieler Zuschauer bleibt in diesem Falle das Wasser im Glas, solange dessen Öffnung noch gänzlich unter Wasser liegt. Auf Basis dieses Phänomens führte Wagenschein Sokratische Gespräche mit den Seminarteilnehmern, die den Grund für das Verbleiben des Wassers im Glas zu erschließen suchten.[4]
Im Jahr 1983 bestritt Wagenschein eine Tagung in Darmstadt unter Anwesenheit und Beteiligung von Otto Herz und Horst Rumpf sowie den Lehrerinnen und Lehrern zweier Alternativschulen, der Glockseeschule und der Freien Schule Frankfurt, in der er dieses Exempel inszenierte. Beim ebenfalls anwesenden Hans Christoph Berg sollte dieses Ereignis nachhaltige Folgen haben und kann als Gründungsmoment der Lehrkunstdidaktik angesehen werden. Berg erinnerte sich später:
„Ach – so kann man Pascals Barometererfindung lehren – mit Bierglas und Wasserschüssel? Muss man nicht vorher den Luftdruck erklären und exakt experimentieren? Kann man ihn so entdecken lassen? Man kann! Und nicht nur Wagenschein kann das. Er hat das Barometerlehrstück so gut komponiert (Aeschlimann hat’s dann auskomponiert), dass wir es wiederholt erfolgreich unterrichtsinszenieren konnten.
(...)
Methode in Exempeln, Exempel mit Methode. In der Didaktik ist das bislang leider noch ungeläufig. Aber hierin richtet sich die Lehrkunst nach der Praxis der anderen Künste: Niemand würde bei Brecht nur seine Theaterkonzeption studieren ohne seine Theaterstücke, niemand würde nur Schumanns Musiktheorie studieren ohne seine musikalischen Werke, oder Paul Klees ‚Bildnerisches Denken’ ohne seine bildnerischen Werke, oder Lessings Dramaturgie ohne seine Dramen: Die Entdeckung und unterrichtspraktische Nutzung der Werke samt Werktradition auch in der Didaktik: das ist das Heureka der Lehrkunstdidaktik – dank Wagenschein!“
Das Lehrstück
.jpg.webp)
Nachdem im Jahr 1995, herausgegeben von Hans Christoph Berg und Theodor Schulze, im Hauptwerk Lehrkunst. Lehrbuch der Didaktik. die ersten elf Lehrstücke vorgestellt waren, erschien zwei Jahre später unter identischer Herausgeberschaft der Band Lehrkunstwerkstatt I.[6] In diesem werden drei weitere Lehrstücke deutlich ausführlicher dargestellt wurden als im Vorgängerband. Ueli Aeschlimann stellt das Barometerlehrstück vor; als Koautor wird Berg geführt, ferner wird Aeschlimanns Inszenierung insbesondere von Horst Rumpf kommentiert.
Aeschlimanns dokumentierte Inszenierung fand vor einer 10. Klasse des Berner Lehrerseminars statt. Rumpf zeigt sich verblüfft darüber, dass Aeschlimanns sokratisches Gespräch trotz der frühzeitigen andeutungsweisen Nennung der eigentlichen Kernerkenntnisse durch einige der Absolventen „noch ein so interessantes, vielgliedriges und lebendiges Unterrichts-Denken sozusagen ausgebrochen ist“.[7] Heiner Ullrich, der im Jahr 2001 die Lehrkunstwerkstätten I–III für die renommierte Zeitschrift für Pädagogik rezensierte, stellt dort besonders heraus, dass Aeschlimann die Absolventen in sogenannten „Zwischenhalten“ durch protokollartige eigene Hefteinträge den jeweils momentanen Erkenntnisstand sichern lässt, wodurch der individuelle Lernprozess dokumentiert werde. Auch hebt er „bewundernswerte eigene Einfälle“ wie den Schlauchversuch hervor und attestiert dem Autor, „Ernst mit Wagenschein“ zu machen.[8]
Pascals Barometer wurde auch eines von drei dokumentierten Lehrstücken in Aeschlimanns zweiter Dissertation von 1999, für die, neben dem standardmäßigen Erstgutachter Berg, Wolfgang Klafki als Zweitgutachter gewonnen werden konnte.[9]
Erst ein gutes Jahrzehnt später, im Jahr 2013, wurde das Lehrstück wieder aufgegriffen und neuinszeniert, und zwar in der Zweitdissertation von Marc Eyer, ebenfalls Berner, die, nachdem sich Klafki altersbedingt ab etwa 2007 zurückgezogen hatte, dessen früheren Schüler Heinz Stübig als Zweitgutachter hatte. Eyers Inszenierung richtet sich an eine 9. Klasse des Gymnasiums Neufeld und weicht auch deshalb etwas von Aeschlimanns ab.[10] Noch vor Abschluss der Dissertation gaben Eyer und Aeschlimann, auf Initiative des Erstgenannten, ein gesondertes Buch zum Lehrstück heraus, das beide Varianten wie auch eine weitere an der Kantonsschule Solothurn durch Fabienne Freiburghaus dokumentiert, analysiert und vergleicht.[11]
Weitere Inszenierungen sind nur in internen Skripten und grauen Publikationen dokumentiert. So entwickelte Björn Gemmer, einer der beiden Schulleiter des Landschulheims Steinmühle im Süden Marburgs, eine schulinterne eigene Variante für den Projektunterricht der 8. Klasse.[12]
Dramaturgie
Pascals Barometer ist in der Hauptsache aus modifizierten historischen Versuchen des 17. Jahrhunderts aufgebaut, die durch aktuelle Beobachtungen ergänzt werden. Die Aufteilung in Akte ist bei Aeschlimann und Eyer auch intern nicht einheitlich bzw. wird auch zwischen den einzelnen Darstellungen modifiziert. Da der Fundus der Experimente in der Hauptsache immer der gleiche ist, werden die Fundamentalversuche nachfolgend in einer sinnvollen Reihenfolge[13] abgehandelt, von der in Teilen auch abgewichen werden kann. Wichtig ist, dass Bierglas- und Wasserschlauchexperiment vornean gestellt werden und die Experimente von von Guericke und Boyle, die bereits eine Vakuumpumpe benötigen, am Ende stehen. Hauptquellen der nachfolgenden Unterabschnitte sind die Lehrkunstwerkstatt I, die Zweit-Dissertationen von Aeschlimann und Eyer sowie ihr gemeinsames Buch zum Lehrstück.[14]
Wagenscheins Bierglasexperiment
.jpg.webp)
Ganz am Anfang steht das aus dem Becken gezogene Bierglas, das auch unmittelbar die organisierende Sogfrage stellt:
- „Warum bleibt das Wasser im Glas und fließt nicht ins Becken?“
Idealerweise, aber auch real mehrfach in der Form geschehen, kristallisieren sich unter den Lernenden zwei mögliche Erklärungen heraus:
- Das Ausfließen des Wassers würde ein Vakuum erzeugen, was dem horror vacui widerspräche.
- Der Luftdruck hält die Wassersäule oben.
Obwohl die zweite Erklärung zutrifft, widerspricht sie der Intuition: Im täglichen Leben spürt man nichts von der Schwere der Luft. Im sokratischen Gespräch muss nunmehr erörtert werden, welche weiteren Überlegungen und Experimente, welche der beiden Erklärungen stützen würden.
Ein unmittelbares Folgeexperimente ist etwa eine volle Apothekerflasche, deren Wasser von einer winzigen Petrischale gehalten wird. Die Erkenntnis, dass es nicht auf das Wasservolumen, sondern einzig auf die absolute Höhe der Wassersäule ankomme, da bei Verwendung einer Flasche mit kleinem Ausguss der Großteil des Wassers von den Gefäßwänden gehalten werde, kommt im Idealfalle in genetischer Weise von der Schülerseite. Die Frage, wie hoch die Wassersäule maximal werden könne, führt zu Bertis Versuch.
Bertis Wassersäulen und das Schlauchexperiment


Gasparo Berti (ca. 1600–1643) hatte im Jahr 1641 in Rom die maximale Höhe einer Wassersäule demonstriert und gleichzeitig versucht, ein Vakuum herzustellen. Dazu verwendete er eine knapp 12 m hohe Konstruktion mit einem Bleirohr, oberhalb dessen eine gläserne Phiole luftdicht angebracht war und die nach unten in eine mit Wasser gefüllte Schüssel ragte. Gefüllt wurde von oben (C), während das Rohr unten (R) verschlossen war. Anschließend wurde oben verschlossen und der Hahn unten freigegeben. Das Wasser senkte sich auf eine Höhe von 18 Ellen (9,7 m), die zuvor bereits u. a. Galileo Galilei als maximale Ansaughöhe von Pumpen bekannt gewesen war.
Um zu beweisen, dass oberhalb der Wassersäule ein Vakuum entstehe, platzierte Berti auf Anregung von Athanasius Kircher ein magnetisch betriebenes Glöckchen (M) im Inneren der Phiole. Dieser Beweis misslang indes, da der Klang der Glocke klar vernehmbar war, was auf das Vorhandensein von Luft schließen ließ. Dies dürfte an einer verminderten Dichtigkeit der Konstruktion gelegen haben, die auf Dauer auch dazu führte, dass die Wassersäule sank.[16]
Bertis Versuch lässt sich heute deutlich einfacher nachstellen. Hierzu wird ein 12 bis 15 m langer, durchsichtiger Schlauch ganz mit Wasser gefüllt, an der Oberseite verschlossen und diese dann in einem Treppenhaus nach oben transportiert, bis die Wassersäule bei etwa zehn Metern stehenbleibt – selbst wenn man das Schlauchende weiter anhebt. Damit erhält man ein Maß dafür, wie weit sich das Wasser in einem fiktiven, extralangen Bierglas maximal in die Höhe ziehen ließe. Unklar bleibt indes, ob oberhalb des Wassers ein Vakuum entsteht oder aber etwa Wasserdampf.
Chronologisch fand Bertis Versuch nach der Veröffentlichung von Galileis unten dargelegten Überlegungen statt, die für Berti auch Motivation gewesen waren.[17] Im Lehrstück folgt er jedoch unmittelbar auf das Bierglasexperiment, das er verallgemeinert.
Galileis begrenzte Kraft des Vakuums
Galileo Galilei (1564–1642) hatte im Jahr 1633 (bzw. 1638)[18] das Buch Discorsi e Dimostrazioni Matematiche intorno a due nuove scienze verfasst. Er war zu diesem Zeitpunkt kein Vertreter der Luftdrucktheorie, zweifelte jedoch auch die Theorie des horror vacui an. Vielmehr glaubte er daran, dass eine feste Kraft existiere, mithilfe der man ein Vakuum erzeugen könne. Als Versuchsaufbau schlug er einen mit Wasser gefüllten Zylinder vor, der durch einen Kolben verschlossen werde, nachdem alle Luft herausgelassen sei. Drehe man den Zylinder nunmehr um, so könne man durch an den Kolben angehängte Gewichte die „Kraft des Vakuums“ messen.[19]
Die Kraft des Vakuums lässt sich auch mit einfacheren Methoden messen. So kann man an einer Plastikspritze, deren Ende zugehalten wird, mit einer Federwaage ermitteln, welche Kraft notwendig ist, um den Kolben herauszuziehen. Diese Kraft ist offenbar proportional zur Bohrung, d. h. zur Querschnittsfläche der Spritze.
Torricellis Barometer und der Schweredruck
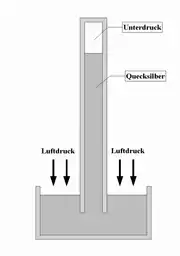
Evangelista Torricelli (1608–1647) war ein Schüler Galileis. Im Jahr 1643 baute er Bertis Wassersäulenversuch mit dem 13–14 mal schwereren Quecksilber nach, womit er insbesondere das Barometer erfand. Es stellte sich heraus, dass die maximale Höhe der Quecksilbersäule bei Normaldruck etwa 760 mm, also den dreizehnten bis vierzehnten Teil von 10 m, beträgt.
Diese Erkenntnis führt zum Begriff des Schweredrucks. Sie legt die Vermutung nahe, dass auch die über uns stehende Luft ein Gewicht habe, das pro Flächeneinheit exakt 760 mm Quecksilber oder 10 m Wasser entspreche. Man kann, etwa durch Vergleich einer (teilweise) luftleer gepumpten Flasche mit derselben in luftgefüllt, die Dichte von Luft zu etwa 1,3 Gramm pro Liter berechnen, was etwa dem 800-sten Teil der Dichte von Wasser entspricht. Entsprechend müsste die Luft 8 km hoch stehen, um mit der gleichen Kraft pro Fläche auf ihre Unterlage zu drücken. Dass die Erdatmosphäre noch weiter reicht, hängt auch damit zusammen, dass Luft, anders als Flüssigkeiten, relativ kompressibel ist und die Luftdichte mit der Entfernung zur Erde abnimmt.
Von Torricelli stammt das folgende Zitat, das sich nunmehr aufdrängt:
„Wir leben untergetaucht auf dem Grund eines Meeres von elementarer Luft.“
Pascals Demonstration am Puy de dôme

Blaise Pascal (1623–1662) hatte im Jahr 1647 bereits durch seinen Versuch Leere in der Leere nachgewiesen bzw. plausibel gemacht, dass über den Wasser- und Quecksilbersäulen ein Vakuum entstehe. Darüber hinaus soll er im folgenden Jahr mit Freunden gewettet haben, er könne mit einem Glas Wein ein volles Fass Wein zum Bersten bringen. Dies gelang ihm durch einen entsprechenden Höhenunterschied (s. links).

Deutlich bekannter wurde indes sein Versuch im französischen Zentralmassiv, den er durch seinen Schwager Florin Périer im selben Jahr (1648) durchführen ließ. Périer hatte die Aufgabe, ein Quecksilbermanometer von der Stadt Clermont-Ferrand bis hinauf auf den etwa 1000 m höheren Puy de Dôme (1465 m) zu transportieren und dabei den Stand der Quecksilbersäule regelmäßig zu dokumentieren. Der Schweredruck, so er denn verantwortlich sein sollte, müsse Pascals Überlegungen nach in größerer Höhe geringer sein, da dort eine geringere Menge Luft auf dem Beobachter laste.[21]
Pascals Vermutung bestätigte sich. Abgesehen von der Höhenabhängigkeit des Luftdrucks erkannte er auch, dass das Wetter vom Luftdruck abhänge, und bahnte so die Nutzung des Barometers für die Wettervorhersage an.
Da Quecksilberthermometer sperrig sind und man heute auch nicht mehr so unbedarft mit dem giftigen Metall umgeht wie zu Pascals Zeiten, wird man im Unterrichtsbetrieb Périers Experiment nicht am lokalen Hausberg durchführen. Jedoch ist auch bei einem Höhenunterschied von z. B. 20 m, wie er innerhalb eines Schulgebäudes meistens herstellbar ist, ein entsprechender Unterschied der Quecksilbersäule im Millimeterbereich messbar.
Guerickes Halbkugeln und die Kraft des Vakuums

Im Jahr 1649 erfand Otto von Guericke (1602–1686) die Luftpumpe, indem er das für Wasser schon länger in Verwendung stehende Prinzip der Hubkolbenpumpe auf Gase ausweitete. Nunmehr war es möglich, mit einfachen Mitteln ein annäherndes Vakuum zu erzeugen.
Ein besonders eindringliches Vorführexperiment zur „Kraft des Vakuums“[23] inszenierte er ab dem Jahr 1856 mit den Magdeburger Halbkugeln. Zwei nur durch luftdichtes Anliegen zu einer Kugel vereinte Halbkugeln wurden luftleer gepumpt. Nunmehr schafften es nicht einmal zwei Gespanne mit je 8 Pferden, in späteren Versuchen waren es gar zweimal 15 Pferde, die Halbkugeln voneinander zu trennen.
In üblichen Sammlungen von Schulen finden sich zumeist deutlich verkleinerte Kopien der Halbkugeln, die statt des originalen Durchmessers von 42 cm nur einen Bruchteil dessen aufweisen. Doch auch Halbkugeln mit einem Innendurchmesser von z. B. 10 cm verschließen noch eine Fläche von knapp 80 cm²=0,008 m². Multipliziert man diese mit dem Druck von 1 bar = 100.000 Pascal, so ergibt sich rechnerisch eine Kraft von knapp 800 Newton, was einer Gewichtskraft von immerhin 80 kg entspricht. Die originalen Halbkugeln brachten es gar auf rund 1,4 t!
Von Guerickes Versuch setzt im Grunde wieder bei Galileis „Kraft des Vakuums“ an und ist rechnerisch ähnlich einfach zu bewältigen wie das Ziehen einer vorne verschlossenen Spritze bekannten Querschnitts, ist jedoch für Schüler ungleich schwieriger fassbar. Während man den Kolben einer Spritze tatsächlich einige Zentimeter ziehen kann, ohne dass Luft eindringen könnte, lassen sich die Halbkugeln im Grunde nur infinitesimal weit ziehen, bevor eindringende Luft das Vakuum zerstören würde. Auch ist dem Lernenden mitunter nicht sofort klar, dass die Kraft auf die innere Querschnittsfläche der Kugel wirkt, obwohl der äußere Luftdruck unmittelbar zunächst auf die Halbkugelsphären drückt. Der sehr kontraintuitive Versuch bedarf daher einer eingehenderen Untersuchung und Erklärung. Solange die Kugel mit Luft atmosphärischen Druckes gefüllt ist, drückt die innere Luft die Kugelhälften exakt mit der Kraft auseinander, mit der die Außenluft sie zusammendrückt. Erst durch das Auspumpen der Kugel verfällt dieses Gleichgewicht, bis von innen annähernd keine Gegenkraft mehr vorliegt.
Boyles Demonstration und die Rückkehr zum Bierglasexperiment
.jpg.webp)
Robert Boyle (1627–1692) nutzte von Guerickes Erfindung der Luftpumpe im Jahr 1660, indem er die Säulenhöhe eines Barometers unter einer Glasglocke beobachtete, die mit einem Unterdruck versehen wurde. Ein analoger Versuch lässt sich in der Schule mit einem verkleinerten „Wasserbarometer“, also einer Miniatur des Bierglasversuchs, anstellen. Bei hinreichendem Unterdruck fließt das Wasser selbst aus einem nur wenige cm langen Miniaturglas. Damit schließt sich der Kreis, der im Bierglasversuch seinen Anfang nahm.
Finale und mögliche Ausblicke
Während Ueli Aeschlimann in seinem Finale die gewonnenen Erkenntnisse unmittelbar auf den Zusammenhang zwischen Luftdruck und Wetter anwendet, präferiert Marc Eyer eine Abschlussdiskussion der historischen Protagonisten des Lehrstücks, in deren Rollen einzelne Schüler schlüpfen.
Bereits in den eigentlichen Inszenierungen werden mitunter auch Betrachtungen zu Alltagsphänomenen angestellt, die von den oben dokumentierten historischen Versuchen abweichen. Zu nennen wären das Prinzip des Wasserturms, kommunizierende Röhren wie der Siphon und die Schlauchwaage, der Trinkhalm sowie das Prinzip der Hydraulik. Auch verschiedene weitere Barometertypen, darunter das Goethe-Barometer und das Dosenbarometer, werden üblicherweise vorgestellt und analysiert; als geschaffenes Werk kann u. U. ein selbstgebautes Membran-Barometer mitgenommen werden.
Das Lehrstück kann auch als Basis für die Behandlung der Gasgesetze herangezogen werden, die deutlich stärker quantitativ-mathematischer Verfahren bedürfen.[24]
Literatur
Die folgende Aufstellung ist chronologisch geordnet:
- Galileo Galilei: Discorsi e Dimostrazioni Matematiche intorno a due nuove scienze. Rom 1633
- Blaise Pascal: Lettre de Monsieur Pascal jeune a Monsieur Perier, du 15 novembre 1647, in Brunschvigg, Boutroux Oeuvres de Blaise Pascal, Band 2, S. 153–162, Archive – dokumentiert insbesondere Leere in der Leere; s. Berg/Schulze (1997)
- Caspar Schott: Technica curiosa, sive mirabilia artis. Endterus, Nürnberg 1664
- Robert Boyle: Hydrostatical paradoxes, made out by new experiments … 1666. (online).
- Otto von Guericke: Neue „Magdeburgische“ Versuche über den leeren Raum. Reihe Ostwalds Klassiker, Bd. 59. Thun, Frankfurt/M. 1996, ISBN 3-8171-3059-7; Übers. von: Ottonis De Guericke Experimenta nova Magdeburgica de vacuo spatio, Waesberge, Amsterdam 1672.
- Ernst Mach: Die Mechanik in ihrer Entwicklung. Edition Classic Verlag Dr. Müller, Saarbrücken 2006 (Reprint der 9. Auflage 1933; orig. 1883); ISBN 978-3-86550-525-5
- Martin Wagenschein: Erinnerungen für morgen. Eine pädagogische Autobiographie. Beltz, Weinheim/ Basel 1983, ISBN 3-407-83075-0; darin:
- Junge Schweizer (PDF; 120 kB; S. 116–119)
- Hans Christoph Berg, Theodor Schulze (Hrsg.): Lehrkunstwerkstatt I, Didaktik in Unterrichtsexempeln, mit einer Einführung von Wolfgang Klafki. Luchterhand, Neuwied 1997; ISBN 978-3-472-03010-2; darin:
- Pascals Barometer (S. 81–124)
- Hans Christoph Berg, Theodor Schulze: Editorial (S. 83–84)
- Blaise Pascal: Briefliche Bitte um experimentelle Untersuchung des Luftdrucks (an Florin Périer; S. 85–86)
- Florin Périer: Bericht über die Barometerbeobachtungen am Fuße und auf dem Gipfel des Puy de Dôme (an Blaise Pascal; S. 86–88)
- Susanne Mumm: Im Seminar bei Martin Wagenschein (S. 88–89)
- Ueli Aeschlimann mit Hans Christoph Berg: Pascals Barometer. Ein Lehrstück nach Wagenschein. (S. 90–116)
- Horst Rumpf: Ein kleiner Kommentar zu „Pascals Barometer“ (S. 116–119)
- Peter Gasser: Fallstudie zum Lehrstück „Pascals Barometer“ (S. 119–12)
- Pascals Barometer (S. 81–124)
- Ueli Aeschlimann: Mit Wagenschein zur Lehrkunst. Gestaltung, Erprobung und Interpretation dreier Unterrichtsexempel zu Physik, Chemie und Astronomie nach genetisch-dramaturgischer Methode. Marburg 1999; DNB 969920059 (Download der Original-Dissertation), darin:
- „Pascals Barometer“ – ein erstes Lehrstück (S. 15–61)
- Heiner Ullrich: Lehrkunstwerkstätten I–III (Berg/Schulze 1997 und 1998, Berg/Klafki/Schulze 2000) in: Zeitschrift für Pädagogik, Heft 4 (2001) (PDF; 1,0 MB); das Barometerlehrstück wird auf S. 611 besprochen
- Schweizerische Konferenz der kantonalen Erziehungsdirektoren (EDK; Hrsg.): Unterrichtsentwicklung – zum Stand der Diskussion. Studien und Berichte 2. Biel/Bern 2004 (EDK-Bericht 2004)
- Marc Eyer, Ueli Aeschlimann (et al): Pascals Barometer. hep (Band 8), Bern 2013; ISBN 978-3-0355-0008-0
- Marc Eyer: Lehrstückunterricht im Horizont der Kulturgenese. Lehrkunstdidaktische Komposition und Inszenierung von Galileis Fallgesetz – Pascals Barometer – Fermats Spiegeloptik. Marburg 2013; DNB 1049818873 (Download der Original-Dissertation), darin:
- Pascals Barometer (S. 79–145)
- Marc Eyer: Lehrstückunterricht im Horizont der Kulturgenese. Ein Modell für lehrkunstdidaktischen Unterricht in den Naturwissenschaften. Springer, Wiesbaden 2015; ISBN 978-3-658-10997-4 (Nachdruck von Eyer (2013))
- Björn Gemmer: Pascals Barometer. Physik-Projekt für die achte Klasse zur Einführung in die Aero- und Hydrostatik. Skript, Marburg 2016
Weblinks
- Pascals Barometer auf lehrkunst.ch
- Ueli Aeschlimann: Mit Wagenschein zur Lehrkunst. Gestaltung, Erprobung und Interpretation dreier Unterrichtsexempel zu Physik, Chemie und Astronomie nach genetisch-dramaturgischer Methode. Marburg 1999; DNB 969920059 (Download der Original-Dissertation)
- Marc Eyer: Lehrstückunterricht im Horizont der Kulturgenese. Lehrkunstdidaktische Komposition und Inszenierung von Galileis Fallgesetz – Pascals Barometer – Fermats Spiegeloptik. Marburg 2013; DNB 1049818873 (Download der Original-Dissertation), darin:
- Pascals Barometer (S. 79–145)
- Heiner Ullrich: Lehrkunstwerkstätten I–III (Berg/Schulze 1997 und 1998, Berg/Klafki/Schulze 2000) in: Zeitschrift für Pädagogik, Heft 4 (2001) (PDF; 1,0 MB); das Barometerlehrstück wird auf S. 611 besprochen
Fußnoten
- Ueli Aeschlimann an der PH Bern, Memento vom Februar 2017
- Marc Eyer (Memento des Originals vom 13. Februar 2017 im Internet Archive) Info: Der Archivlink wurde automatisch eingesetzt und noch nicht geprüft. Bitte prüfe Original- und Archivlink gemäß Anleitung und entferne dann diesen Hinweis. an der PH Bern
- siehe en:Gasparo Berti
- vgl. Wagenschein (1983), S. 116–119
- s. EDK (2004), S. 85f.
- s. Berg/Schulze (1997)
- s. Rumpf in Berg/Schulze (1997)
- vgl. Ullrich (2001), S. 611
- s. Aeschlimann (1999), S. 15–61
- s. Eyer (2013), S. 79–145
- s. Eyer/Aeschlimann (2013)
- vgl. Gemmer (2016)
- Die hier dargestellte Reihenfolge entspricht der des Abschnitts Das Lehrstück auf einer Doppelseite aus Eyer/Aeschlimann (2013), S. 12–13.
- Vgl. Aeschlimann in Berg/Schulze (1997), Aeschlimann (1999), Eyer (2013) sowie Eyer/Aeschlimann (2013).
- s. Schott (1664)
- Eine Darstellung findet sich auch in Friedrich Jaegers Enzyklopädie der Neuzeit 13, Metzler, Stuttgart 2011; ISBN 978-3-476-02003-1 (Google Books).
- Siehe etwa History of the Barometer auf strange-loops.com
- Im Jahr 1633 hatte Galilei das Buch verfasst, es wurde jedoch aufgrund seines Hausarrestes zunächst nicht publiziert; 1635 erschien in Straßburg eine lateinische Übersetzung und erst 1638 folgte die italienische Version.
- vgl. Galilei (1633), S. 14–15 bzw. Aeschlimann (1999), S. 59–60 nebst Skizze
- zitiert aus Shmuel Sambursky: Der Weg der Physik; S. 337; vgl. auch Aeschlimann (1999), S. 55
- vgl. Pascal (1647) bzw. Pascal in Berg/Schulze (1997)
- s. von Guericke (1672)
- Streng genommen handelt es sich selbstredend um die Kraft des Druck(unterschied)es; von Guerickes Pumpe war nicht imstande, ein totales Vakuum zu erzeugen, wohl aber einen Unterdruck von annähernd 0 bar.
- Gemmer hat gar die elementaren Gasgesetze ins Lehrstück integriert, was allerdings den genetischen Ablauf etwas behindert; vgl. Gemmer (2016).