Optischer Spalt

Als optischen Spalt oder Schlitzblende bezeichnet man in der Optik eine Blende mit einer schmalen, länglichen, meist rechteckigen Öffnung. Schlitzblenden werden oft zum Selektieren erwünschter Lichtspektralanteile, zum Ausblenden unerwünschten Lichts oder zur Strahlformung verwendet.

Typische Ausführung eines rechteckigen optischen Spalts (Schlitzblende) mit über vier Schrauben (in x- und y-Richtung) justierbaren Kanten für optische Laboraufbauten

Technischer Aufbau

Schlitzblenden werden als Lichtdurchlass in einem ebenen Träger realisiert. Im Labor wurde früher eine beispielsweise mit Ruß geschwärzte Glasplatte (ggf. in einem Diarahmen) verwendet, auf der mit einem spitzen Gegenstand (Skalpell, Messer) die Schwärzung in der gewünschten Durchlassform (Linie, Rechteck, …) abgetragen wurde. Heute wird die Blende meist aus Metallplatten, die oft zum Spalt hin keilförmig verdünnt werden (wie z. B. die Schneide einer Schere), als einstellbarer Luftspalt (siehe Bild ganz oben) ausgeführt. Um Reflexionen an den Kanten der Blenden zu vermeiden und um eine gut definierte Position der Spaltblende im Raum zu ermöglichen, werden die Blendenblätter meist als dünne Bleche (maximal wenige Millimeter dick) ausgeführt.

Zur Vermeidung von Streulicht und Blendlicht sind die nicht lichtdurchlässigen Teile meist mattschwarz gehalten, gelegentlich auch aufgeraut.

Durch ein zweites Paar Metallplatten lässt sich oft zusätzlich die Höhe der Spaltöffnung einstellen. Wie bei der Spaltbreite geschieht das in der Regel von Hand per Stellschrauben, da das höchstens einmal je Messreihe verstellt wird. Eine kontinuierliche Verstellung, die einen Servoantrieb nötig machen würde, kommt selten vor.

Intensitätsverteilung hinter Schlitzblenden

Allgemeines

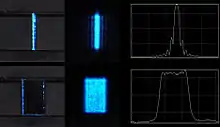
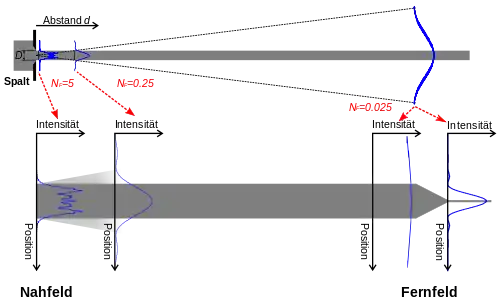
Intensitätsverteilung hinter einem schmalen (oben) und breiten (unten) Spalt, bei Beleuchtung mit einem Laser. Links ist der Spalt zu sehen, in der Mitte ein Foto und rechts die vertikal aufsummierte Intensitätsverteilung.

Wird eine Schlitzblende zur Strahlformung eingesetzt und ihre Öffnung mit kohärentem Licht ganz ausgeleuchtet, so können Beugungseffekte eine wichtige Rolle spielen. Um diese Effekte zu beschreiben, muss das Licht im Rahmen der Wellenoptik betrachtet werden. Die Stärke und Sichtbarkeit dieser Effekte hängt wesentlich von der Fresnel-Zahl $N_{\text{F}}$ ab, die das Verhältnis aus Breite $D$ des Spalts, Wellenlänge $\lambda$ des eingestrahlten Lichts und Abstand $d$ des Beobachters vom Spalt beschreibt:

N_{\text{F}}={\frac {(D/2)^{2}}{\lambda \cdot d}}

Die Intensitätsverteilung lässt sich mit dem Beugungsintegral berechnen. Dabei wird angenommen, dass sich von jedem Punkt des Spaltes aus eine Kugelwelle ausbreitet. Das Beugungsintegral berechnet dann die Summe über alle diese Kugelwellen. Die folgende Abbildung zeigt (numerische) Ergebnisse für verschiedene Abstände $d$ (Fresnel-Zahlen $N_{\text{F}}$ ) des Beobachters vom Spalt:[1]

Abb 1: Feldverteilung im Nahfeld und Fernfeld eines optischen Spalts, der von einer ebenen Welle beleuchtet wird.

Auch für die Beugungserscheinungen am optischen Spalt gilt das babinetsche Prinzip, somit ist das entstehende Beugungsbild gleich dem eines geraden Drahtes.

Nahfeld

Nahfeld-Beugungsbild eines Einzelspalts

Für große Fresnel-Zahlen gibt die Intensitätsverteilung die in Dunkelgrau angedeutete Spaltform gut wieder. Die Schwankungen auf dem Plateau der Intensitätsverteilung rühren von der Beugung an den Spaltkanten her.[2] In diesem Regime (Geometrische Optik) sind Beugungseffekte meist vernachlässigbar. Je nach Breite des Spalts kann dieses Regime auch noch in großer Entfernung vom Spalt auftreten. So ist z. B. bei grünem Licht ( $\lambda =500\;\mathrm {nm}$ ) für einen $D=10\;\mathrm {mm}$ breiten Spalt $N_{\text{F}}>10$ noch für den Abstand $d=5\;\mathrm {m}$ gegeben.

Fernfeld

Abb. 2: Beugungsbild im Fernfeld einer Rechteckblende (oben vergrößert dargestellt)

Abb. 3: Fernfeld-Beugungsbild eines Einzelspalts mit Erläuterungen zur Herleitung der Beugungsminima und -maxima

Abb. 4: Wellenfronten hinter einer Öffnung, die viermal so breit ist, wie die Wellenlänge. Grau bedeutet verschwindende Amplitude.

Für schmale Spalte mit einer Spaltbreite D in der Nähe der Wellenlänge (z. B. D = 10·λ = 5 µm) liegt dagegen das Fernfeldbild (hier $N_{\text{F}}<0{,}01$ ) schon sehr nah hinter dem Spalt (im Beispiel etwa d = 1,25 mm), und praktisch wird dann ausschließlich dieses beobachtet. Die herausstechendste Eigenschaft dieses Fernfeldes ist seine starke Verbreiterung gegenüber der Spaltbreite, was in obiger Abbildung 1 durch die zwei unterschiedlich skalierten Graphen für $N_{\text{F}}=0{,}025$ angedeutet ist. Das Beugungsbild im Fernfeld wird über die Fraunhofer-Näherung für das Beugungsintegral (siehe dort) berechnet. Dieses ergibt das Beugungsbild als Fourier-Transformation der Form des Blendendurchlasses. Ein Beispiel ist rechts dargestellt.

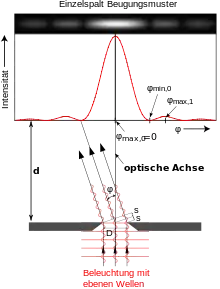
Oft genügt es, die Betrachtung auf eine Ebene parallel zur Ausbreitungsrichtung des Lichtes zu beschränken. Dann kann man das Bild berechnen, das sich einem Beobachter hinter dem Spalt zeigt. Betrachtet man diesen unter dem Winkel $\varphi$ zur optischen Achse (siehe Abbildung 3 rechts), so erhält man:[3]

I(\varphi )\propto \left({\frac {\sin(\pi D\cdot \sin(\varphi )/\lambda )}{\pi D\cdot \sin(\varphi )/\lambda }}\right)^{2}=\operatorname {si} ^{2}\left({\frac {\pi D\cdot \sin(\varphi )}{\lambda }}\right)=\operatorname {sinc} ^{2}\left({\frac {D\cdot \sin(\varphi )}{\lambda }}\right)

Für kleine Abstände $x=d\cdot \tan \varphi$ von der optischen Achse lässt sich die Verteilung der Intensität entlang einer Achse parallel zur Spaltebene näherungsweise angeben:[4]

I(x)\propto \left({\frac {\sin(\pi Dx/(\lambda d))}{\pi Dx/(\lambda d)}}\right)^{2}=\operatorname {si} ^{2}\left({\frac {\pi Dx}{\lambda d}}\right)=\operatorname {sinc} ^{2}\left({\frac {Dx}{\lambda d}}\right)

Diese Verteilung wird auch als Spaltfunktion (siehe auch Sinc-Funktion si(x), bzw. sinc(x)) bezeichnet und ist im oberen Teil von Abbildung 3 rechts dargestellt. Einige Eigenschaften (Minima) dieser eindimensionalen Intensitätsverteilung lassen sich auch anschaulich herleiten. Sie haben für schnelle Abschätzungen (der Abstand der zwei Minima nahe bei $\varphi =0$ kann als Maß für die Größe des Beugungsbildes verwendet werden) und als lehrreiche Anwendung der Prinzipien der Beugung an einer Blende sehr große Bedeutung:

Dazu folgt man dem Huygens-Prinzip und nimmt an, dass von jedem Punkt der Blende eine Kugelwelle ausgeht. Diese Wellen breiten sich unabhängig aus und interferieren beim Beobachter. Der Beobachter sehe nun den Spalt unter einem Winkel φ (siehe unterer Teil der Abbildung 3 rechts). Ist der Gangunterschied 2s (siehe unterer Teil der Abbildung 3 rechts) zwischen den Strahlen von den Spalträndern gerade die Wellenlänge λ, so kann man den Strahl in zwei Teilbündel aufteilen. Zu jedem Teilstrahl des ersten Bündels findet sich dann immer genau ein Teilstrahl im zweiten Bündel, mit einem relativen Gangunterschied von λ/2. Diese zwei Teilstrahlen interferieren also destruktiv und löschen sich aus. Damit wird die gesamte Intensität ausgelöscht und wir beobachten ein Intensitätsminimum. Dieselbe Argumentation gilt, wenn der Gangunterschied zwischen den äußeren Strahlen ein ganzzahliges Vielfaches nλ der Wellenlänge ist; man teilt dann nur in entsprechend mehr Teilbündel n auf. Auch dann findet sich zu jedem Strahl in jedem Teilbündel ein Partner mit Gangunterschied λ/2. Diese Auslöschungsbedingung lautet also (mit dem Gangunterschied s):

\sin \varphi _{\mathrm {min} ,n}={\frac {2s}{D}}=\pm n\cdot {\frac {\lambda }{D}},\quad n\in \mathbb {N}

Man spricht jeweils vom Minimum n-ter Ordnung.

Für die Maxima gibt es keine einfache Herleitung. Sie können über die Extrema der Sinc-Funktion berechnet werden, die detailliert im Artikel zur Sinc-Funktion aufgeführt sind.

Die Intensität dieser Maxima fällt für große Winkel schnell ab. Das Maximum nullter Ordnung ist bei φ=0, also auf der optischen Achse, zu finden.

Besonders die Bedingung für die Minima kann herangezogen werden, um die Verbreiterung der Intensitätsverteilung hinter einem Spalt abzuschätzen. Wie schon oben gezeigt, ist die Fernfeldverteilung sehr viel breiter als der Spalt selbst. Der Öffnungswinkel kann als ${\displaystyle \alpha$ definiert werden und ergibt sich z. B. für einen Spalt mit einer Breite von 10 Wellenlängen (D=10λ, z. B. 5 μm für grünes Licht) zu etwa α=11,5°. Der Lichtstrahl verbreitert sich also sehr schnell hinter dem Spalt. Für einen Spalt von 1000 Wellenlängen (z. B. 0,5 mm für grünes Licht) Breite ergibt sich dagegen nur α=0,1° und man muss den Spalt in sehr großem Abstand beobachten, um eine merkliche Verbreiterung zu beobachten.

Mit Hilfe dieser Formeln kann z. B. die Wellenlänge des auf einen bekannten Spalt fallenden Lichts gemessen werden, indem man den Winkelabstand der Minima n-ter Ordnung misst. Ebenso kann umgekehrt bei bekannter Wellenlänge auf die Breite des Spalts geschlossen werden.

Breite und schmale Spalte

Mit der oft getroffenen Einteilung alleine aufgrund des Verhältnisses der Spaltbreite $D$ zur Wellenlänge λ in breite Spalte (bei denen das Nahfeld dominiert, Beugungserscheinungen also vernachlässigt werden können) und schmale Spalte (bei denen das Fernfeld dominiert) muss vorsichtig umgegangen werden. Diese Unterscheidung ist nämlich, wie oben dargestellt wurde, nicht von der Spaltbreite, sondern von der Fresnelzahl $N_{\text{F}}$ abhängig.

In der Praxis führt diese Ungenauigkeit jedoch selten zu Problemen, da an einem breiten Spalt fast nur das Nahfeld beobachtet wird, während das Fernfeld erst in einem großen Abstand vom Spalt erkennbar wäre. An einem schmalen Spalt hingegen ist das Nahfeld nur in außergewöhnlich geringem Abstand vom Spalt erkennbar, in der Praxis beobachtet man meist das Fernfeld.

Polarisationswirkung

Da die Backen des Spalts meistens aus Metall bestehen, kann dies das durchfallende Licht zusätzlich beeinflussen. Das leitfähige Metall schließt ein elektrisches Feld parallel zu seiner Oberfläche kurz und dämpft dadurch diese Komponente des Lichts. Die Komponente des Lichts, die senkrecht zur Metalloberfläche polarisiert ist, wird praktisch nicht beeinflusst. Es wird also eine teilweise Polarisation mit einer Bevorzugung der E-Feld-Komponente quer zum Spalt vorgenommen. Dies ist allerdings ein kleiner Effekt, der mit vergrößerter Spaltbreite stark abnimmt und keine praktische Anwendung findet. Bei Präzisionsmessungen muss er ggf. mit in die Betrachtung einbezogen werden.

Anwendung

Monochromatoren und Spektrometer

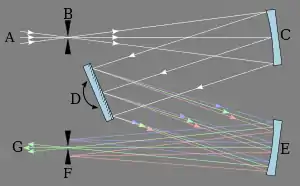
Wellenlängenselektion durch eine Schlitzblende in einem Monochromator: Einfallendes Licht A wird durch ein Gitter D in die Spektralfarben aufgespalten (Dispersion). Das Gitter D wird so gedreht, dass nur Licht der gewünschten Farbe durch den Ausgangsspalt F fällt.

In der Physik werden Schlitzblenden vor allem in Spektrometern und Monochromatoren eingesetzt. Dort dienen sie zur Auswahl eines Teils des zuvor aufgespalteten Lichtspektrums (siehe Abbildung rechts). Ein dispersives Element, wie ein Beugungsgitter oder ein Prisma wird zunächst verwendet, um einfallendes Licht spektral aufzuspalten.[5] Dann wird ein Spektralbereich des Lichts selektiert, indem die anderen Bereiche durch eine Schlitzblende ausgeblendet werden. In Monochromatoren kann so Licht aus einem wählbaren und definierten Spektralbereich erzeugt werden. In Spektrometern wird so eine bestimmte Wellenlänge ausgewählt, mit der die folgende Messung durchgeführt wird. Durch Verschieben des Spaltes oder besser Drehen des dispersiven Elements kann dann das gesamte Spektrum nach und nach aufgezeichnet werden. In der optischen Versuchsapparatur dient die Schlitzblende zudem als sekundäre Lichtquelle für den weiteren Strahlengang.

Ebenso wird die Schlitzblende als sekundäre Lichtquelle auch direkt vor dem dispersiven Element eingesetzt, um auf dessen Eingangsseite für eine definierte Anordnung und Form der Lichtquelle zu sorgen. Dazu wird die Blende von einer breitbandigen (weißen) Lichtquelle bestrahlt, die beispielsweise durch eine Hohlspiegeloptik grob auf den Spalt fokussiert wird.

Bei dieser Verwendung als Strahlbegrenzer würden Beugungseffekte an dem Spalt aber stören. Daher wählt man die Spaltbreite immer ausreichend groß, so dass Beugungseffekte nicht relevant ins Gewicht fallen. Das begrenzt wiederum die erreichbare Wellenlängenauflösung, weshalb ein optimaler Zwischenwert anzustreben ist.

Strahlformung

Schlitzblenden können allgemeiner auch zur Strahlformung eingesetzt werden. Dabei werden sie von hinten großflächig beleuchtet und formen ein rechteckiges Strahlbündel einstellbaren Ausmaßes. So kann verhindert werden, dass Licht auf Teile eines optischen Aufbaus fällt, in dem es durch Streuung oder ungewollte Reflexe stören würde. Dieses Prinzip findet z. B. bei Lichtscheiben-Mikroskopie (SPIM) Anwendung. Hier formt ein einstellbarer Spalt ein rechteckiges Strahlenbündel, das dann mit Hilfe einer Zylinderlinse zu einem Lichtblatt fokussiert wird.[6] Einfacher noch ist die Anwendung im Spaltultramikroskop, in dem ein beleuchteter optischer Spalt mit einer einfachen Kondensor-Linse in eine Probe abgebildet wird. Teilchen, die das so gebildete Lichtblatt durchlaufen können durch ihr Streulicht detektiert werden.[7]

Oft ist die Breite solcher Blenden von Hand einstellbar. Bei Monochromator-Anwendungen wird die Breite dabei dem verwendeten Wellenlängenbereich oder auch der benötigten Intensität angepasst (Auflösung wird beispielsweise geopfert durch eine breitere Einstellung, um mehr Intensität und damit ein besseres Signal-Rausch-Verhältnis zu erzielen). Auch die Höhe des ausgenutzten Spaltmaßes ist oft einstellbar ausgeführt, wieder zur Sicherstellung definierter Verhältnisse beim Strahlbündel.

Bei der Strahlformung sind Spalte meist so breit, dass ein Einzelspalt-Beugungsmuster nicht zu sehen ist. Beugung ist aber weiterhin an den Rändern des Spaltes zu sehen, was zu einem verbreiterten Abfallen der Randintensitäten führt (siehe Bild des breiten Spaltes, ganz oben).

Bildfeldbegrenzung

Umgekehrt werden Blenden auch oft eingesetzt, um Bildfelder einzugrenzen. So kann etwa ein kleiner Bereich aus einem Mikroskopbild ausgeschnitten werden und dann nur auf einen Teil eines Bildsensors abgebildet werden. Mit Hilfe zusätzlicher Optik kann derselbe Bildausschnitt dann etwas versetzt nochmals abgebildet werden. Werden beide Ausschnitte durch unterschiedliche optische Filter gesendet, so kann man denselben Ausschnitt gleichzeitig in mehreren Spektralbereichen aufzeichnen, ohne mehrere Kameras verwenden zu müssen.[8]

Phototechnik

Vertikal bewegter Schlitzverschluss bei einer Belichtungszeit von 1/500s – unten sieht man deutlich den Spalt zwischen den Blendenblättern.

Bei Kameras finden sich breite Schlitzblenden mit größerem Abstand (ca. 0,8 – 1,0 mm) bei Panoramakameras und bei technischen Anwendungen. Sie sind hier auch als Übergang zur elektronischen Zeilenkamera zu sehen. Belichtet wird jeweils ein schlitzförmiger Ausschnitt analog etwa dem Schlitzverschluss, allerdings wird der Film (oder Filmausschnitt durch die Objektivbewegung) während der Aufnahme bewegt.

Einzelnachweise

Bahaa E. A. Saleh, Malvin Carl Teich: Fundamentals of photonics. Wiley-Interscience, 22. Februar 2007, ISBN 978-0-471-35832-9, S. 132–133.
mike-willis.com: Diffraction
Wolfgang Demtröder: Experimentalphysik 2. Elektrizität und Optik. Springer Verlag, 2006, ISBN 3-540-33794-6, S. 322–324.
Christian Gerthsen: Gerthsen Physik. Springer Verlag, 19. August 2003, ISBN 978-3-540-02622-8, S. 523–524 (Abgerufen am 13. August 2011).
Wolfgang Demtröder: Laserspektroskopie: Grundlagen und Techniken. Springer, 1. August 2007, ISBN 978-3-540-33792-8, S. 68–69 (Abgerufen am 13. August 2011).
K. Greger, J. Swoger, E. H. Stelzer: Basic building units and properties of a fluorescence single plane illumination microscope. In: The Review of scientific instruments Band 78, Nummer 2, Februar 2007, S. 023705, ISSN 0034-6748. PMID 17578115.
Nobelpreis-Vorlesung von R. A. Zsigmondy (englisch): Properties of colloids (PDF; 108 kB), mit einer Abbildung und kurzen Erklärung zum Ultramikroskop
K. Kinosita, H. Itoh, S. Ishiwata, K. Hirano, T. Nishizaka, T. Hayakawa: Dual-view microscopy with a single camera: real-time imaging of molecular orientations and calcium. In: Journal of Cell Biology Band 115, Nummer 1, Oktober 1991, S. 67–73, ISSN 0021-9525. PMID 1918140. PMC 228992 (freier Volltext).

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[SalehTeich2007-1] Bahaa E. A. Saleh, Malvin Carl Teich: Fundamentals of photonics. Wiley-Interscience, 22. Februar 2007, ISBN 978-0-471-35832-9, S. 132–133.

[2] -willis.com: Diffraction

[Demtroeder2_2006-3] Wolfgang Demtröder: Experimentalphysik 2. Elektrizität und Optik. Springer Verlag, 2006, ISBN 3-540-33794-6, S. 322–324.

[Gerthsen2003-4] Christian Gerthsen: Gerthsen Physik. Springer Verlag, 19. August 2003, ISBN 978-3-540-02622-8, S. 523–524 (Abgerufen am 13. August 2011).

[Demtröder2007-5] Wolfgang Demtröder: Laserspektroskopie: Grundlagen und Techniken. Springer, 1. August 2007, ISBN 978-3-540-33792-8, S. 68–69 (Abgerufen am 13. August 2011).

[PMID17578115-6] K. Greger, J. Swoger, E. H. Stelzer: Basic building units and properties of a fluorescence single plane illumination microscope. In: The Review of scientific instruments Band 78, Nummer 2, Februar 2007, S. 023705, ISSN 0034-6748. PMID 17578115.

[ultramicroscope-7] Nobelpreis-Vorlesung von R. A. Zsigmondy (englisch): Properties of colloids (PDF; 108 kB), mit einer Abbildung und kurzen Erklärung zum Ultramikroskop

[PMID1918140-8] K. Kinosita, H. Itoh, S. Ishiwata, K. Hirano, T. Nishizaka, T. Hayakawa: Dual-view microscopy with a single camera: real-time imaging of molecular orientations and calcium. In: Journal of Cell Biology Band 115, Nummer 1, Oktober 1991, S. 67–73, ISSN 0021-9525. PMID 1918140. PMC 228992 (freier Volltext).