Optisches Gitter

Optische Gitter, auch Beugungsgitter oder Mehrfachspalt genannt, sind periodische Strukturen zur Beugung von Licht. Alltagsbeispiele sind CDs, feine Kämme sowie feine Gardinen (letztere v. a. nachts an Straßenlaternen o. ä.). Die Gitterkonstante ist die Periode des Gitters, typische Werte sind 0,5 µm bis 10 µm. Alle Typen von Gittern bestehen aus parallelen, linienartigen Strukturen:

Spalte in undurchsichtigem Material oder undurchsichtige Stege auf einer transparenten Platte (Draht-, Spalt- oder Strichgitter)
Stege oder Furchen auf einer reflektierenden Fläche (Reflexionsgitter, Stufengitter)

Mikroskopaufnahme eines Transmissionsbeugungsgitters, wie es im Röntgensatelliten Chandra verwendet wird. Die Gitterkonstante ist 1 µm. Die drei senkrechten Stege sind Teil eines Stützgitters.

Großes Reflexionsgitter

Gitter wirken durch Beugung von kohärentem Licht: Das Licht der einzelnen Spalte interferiert und bildet ein Interferenzmuster. Monochromatisches Licht wird in wenige verschiedene Richtungen (exakt: in Maxima verschiedener Ordnung) abgelenkt. Die Ablenkungswinkel hängen von der Gitterkonstante $g$ und der Wellenlänge $\lambda$ ab, größere Ablenkungswinkel entsprechen höheren Ordnungen $n$ . Polychromatisches (z. B. weißes) Licht wird in sein Spektrum aufgefächert ähnlich wie bei einem Prisma. Ganz nahe am Gitter interferiert das Licht zu Kopien der Gitterstruktur (Talbot-Effekt).

Gitter wurden 1785 von David Rittenhouse erfunden, 1821 baute auch Joseph von Fraunhofer Gitter. In den 1860ern wurden die Gitter mit der kleinsten Gitterkonstanten g von Friedrich Adolph Nobert (1806–1881) in Pommern hergestellt, dessen feinste Gitterlinien mit damaligen Mikroskopen schon nicht mehr aufgelöst werden konnten.[1] Danach übernahmen die beiden Amerikaner Lewis Morris Rutherfurd (1816–1892) und William B. Rogers (1804–1882) die Führung,[2][3] und gegen Ende des 19. Jahrhunderts dominierten die Konkavgitter von Henry Augustus Rowland (1848–1901),[4] mit denen u. a. um 1890 in Baltimore die Rotverschiebung im Sonnenspektrum entdeckt wurde.[5]

Anwendung

Optische Gitter werden in optischen Messeinrichtungen zur Monochromatisierung der Strahlung (Monochromator) sowie zur Analyse von Spektren (optisches Spektrometer) eingesetzt. Ebenso werden damit Laser frequenzstabilisiert (siehe Braggreflektor, DFB-Laser), kurze Laser-Impulse hoher Leistung verstärkt und in Lasershows Punktmuster erzeugt. Ein weiteres Anwendungsgebiet ist die Kanaltrennung bzw. -zusammenführung in der optischen Datenübertragung.

Gittertypen

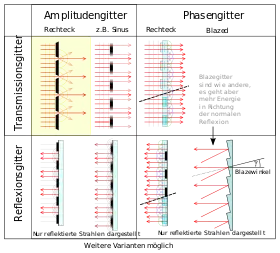
Einteilung von Gittern mit Beispielen.

Unterscheidungsmerkmale für Gittertypen sind:

Herstellungsverfahren: Man unterscheidet zwischen mechanisch hergestellten (z. B. mit Diamantsticheln geteilten) und holografischen (=optisch erzeugten) Gittern. Eine seltener verwendete Methode besteht in der Abbildung von Masken in einen Fotolack.
Funktionsweise: Es wird zwischen Transmissions- und Reflexionsgittern unterschieden.
Transparenz: Es wird zwischen Amplitudengittern (absorbierenden Gittern) und Phasengittern (Umformen der Wellenfront) unterschieden

Eine neuere Entwicklung sind abbildende Gitter, die sowohl holografisch als auch – in Grenzen – durch mechanische Teilung hergestellt werden können.

Ein Spezialfall sind Röntgengitter, bei denen die (Röntgen-)Beugung an den periodischen Gitterstrukturen eines Kristalls geschieht. Weil hier die Gitterkonstanten von der Größenordnung eines Atomdurchmessers sind, eignen diese sich für sehr kurze Wellenlängen.

Transmissionsgitter

Transmissionsgitter sind Amplitudengitter. Sie bestehen aus einer Abfolge von durchlässigen und undurchlässigen Bereichen (Lücken und Stege). Sie besitzen deshalb den inhärenten Nachteil, dass durch die Stege ein Teil des einfallenden Lichts reflektiert oder absorbiert wird und damit nicht zur Intensität des entstehenden Spektrums beiträgt. Bei einem Steg-Lücke-Verhältnis von 1:1 sind das 50 %.

Drahtgitter

1820 benutzte Joseph von Fraunhofer Drähte, die er dicht nebeneinander spannte. Ebenso wirken feine Gewebe (z. B. Regenschirm als Beispiel eines 2D-Gitters).

Ein Drahtgitter ist auch das oben abgebildete Röntgenbeugungsgitter.

Drahtgitter können auch bei Mikrowellen, Millimeterwellen, Terahertzstrahlung und im mittleren/fernen Infrarot zum Einsatz kommen, sie besitzen dann entsprechend große Gitterkonstanten.

Laminargitter

Laminargitter werden dort verwendet, wo es Substratmaterialien gibt, die für den Bereich der Anwendungswellenlängen transparent sind. Sie bestehen dementsprechend aus Streifen aus Metall oder absorbierendem Material, die auf das Substrat aufgebracht bzw. auf diesem erzeugt werden. Die Gitterstrukturen können auf dem Wege der Holografie, d. h. durch Interferenz zweier kohärenter Laserstrahlen, direkt auf einem mit Fotolack beschichteten Glas- oder Kunststoffsubstrat erzeugt werden. Man kann mit dieser Technik Furchendichten bis zu mehreren 1000 Linien pro Millimeter erzeugen.

Reflexionsgitter

Reflexionsgitter sind Phasengitter. Sie funktionieren so, dass für bestimmte Winkel und Wellenlängen Elementarwellen in benachbarten Bereichen (z. B. Steg und Lücke eines Kastenprofils) einen Gangunterschied von einem ganzzahligen Vielfachen der Wellenlänge haben, was zu konstruktiver Interferenz führt. Reflexionsgitter sind im Allgemeinen effizienter als Transmissionsgitter, weil im Idealfall die gesamte Strahlungsleistung – abzüglich des Reflexionsverlusts und eventueller Abschattungsverluste – zur gebeugten Leistung beiträgt.

Mechanisch geteilte Blazegitter

In Monochromatoren und Spektrometern werden häufig so genannte Sägezahn- oder Blazegitter eingesetzt. Dies sind Gitter mit einem Sägezahn-ähnlichen Profil, wobei die an der konstruktiven Interferenz beteiligten Blazeflächen dem langen Schenkel des Sägezahns entsprechen. Der Winkel zwischen Blazefläche und Substrat (der Blazewinkel) kann so gewählt werden, dass möglichst viel Licht einer bestimmten Wellenlänge in eine bestimmte Beugungsordnung fällt. Dies ist dann erreicht, wenn für ein- und ausfallende Strahlung zugleich die Reflexionsbedingung bezüglich der Blazefläche gilt. Im Idealfall kann so eine Beugungseffizienz von 100 % erreicht werden.

Bei der mechanischen Teilung können die Blazewinkel in weiten Bereichen variiert werden, weshalb man die Technik trotz ihrer Nachteile gerne zur Herstellung von Blazegittern verwendet. Bei der mechanischen Teilung werden mit einem geeignet geschliffenen Diamantstichel in einer Metalloberfläche parallele Furchen erzeugt. Dabei wird das zu teilende Material (häufig Gold) plastisch verformt. Bei korrekter Einstellung der Stichelwinkel und geeignetem Diamantschliff erreicht man, dass ein Aufwurf mit sauberem Sägezahnprofil entsteht. Der Physiker Henry Augustus Rowland verbesserte 1882 die Herstellung mechanisch geteilter Gitter entscheidend, indem er die Präzision des Verfahrens erheblich verbesserte; man spricht daher auch von Rowland-Gitter. Außerdem gelang ihm als erstem die Teilung auf konkaven Substraten.

Holografische Gitter

Reflexionsgitter können auch fotolithografisch bzw. holografisch hergestellt werden. Dazu werden zwei kohärente Teilstrahlen eines Lasers im Photolack eines Substrats zur Interferenz gebracht. Das Interferenzmuster erzeugt Bereiche mit starker und schwächerer Belichtung. Bei der anschließenden Entwicklung wird (je nach Art des Entwicklers) einer der beiden Bereiche bevorzugt abgetragen. Es ist unmittelbar einsichtig, dass auf diese Weise Laminarprofile erzeugt werden können. Es ist aber in engeren Grenzen auch möglich, Blazeprofile holografisch herzustellen.

Ein wichtiger Vorteil des fotolithografischen Verfahrens besteht darin, dass Gitter auch auf stark gekrümmten Substratoberflächen hergestellt werden können. Ein weiterer Vorteil mag darin liegen, dass potenziell eine größere Anzahl von Originalen in vergleichsweise kurzer Zeit angefertigt werden kann, wenn der Aufbau erst einmal steht und der Laser stabil arbeitet.

Abbildende Gitter

Die Kombination eines Gitters mit einer konkaven Oberfläche, die also einen Hohlspiegel bildet, hat den Vorteil, dass dadurch die gebeugte Strahlung gleich fokussiert wird, ohne dass weitere optische Elemente nötig sind. Allerdings ist diese Fokussierung noch mit den typischen Abbildungsfehlern eines Hohlspiegels behaftet. Man kann jedoch das Gitterdesign so modifizieren, dass es diese Fehler korrigiert.

Ein weitergehendes Beispiel sind die sogenannten flat-field-Gitter. In dem oben beschriebenen Fall liegen die Fokusse der verschiedenen Wellenlängen nicht auf einer Ebene, sondern auf einer gekrümmten Fläche. Moderne Detektor-Arrays, wie sie gerne in Kompaktspektrometern eingesetzt werden, sind jedoch üblicherweise eben. Deshalb werden die Parameter des Holografieaufbaus so korrigiert, dass die Fokusse aller Wellenlängen eines interessierenden Bereichs in einer Ebene liegen. Bei derartigen Gittern sind die beugenden Strukturen weder gerade noch parallel noch gleichabständig. Es handelt sich bereits um relativ komplexe Hologramme.

Auch mechanisch geteilten Gittern kann eine abbildende Wirkung mitgegeben werden. Bei sogenannten Chirp-Gittern wird die Gitterkonstante nach Vorgabe über die Gitterfläche variiert. Dadurch kann z. B. eine Fokussierung in der Ebene senkrecht zu den Gitterfurchen erzielt werden.

Replika

Zur Produktion größerer Stückzahlen wird auf Replikatechniken zurückgegriffen.

Eine Replika hat interessanterweise eine bessere Qualität (Streulicht und höhere Ordnungen vermindert) als das Original. Bei der Fertigung mit einem Diamantstichel sind die erzeugten Furchen sehr präzise in ihrer Form, aber die Kanten zu den Nachbarfurchen haben einen leichten unvermeidlichen Grat. Durch den Abdruck wird das Problem beseitigt. Jetzt liegen die Kopien der störenden Grate in der „Talsohle“ und die präzisen Furchen bilden die Spitzen des Gitters. Die Abdrücke werden auf eine Glasplatte gekittet und für Reflexionsgitter noch mit Metall bedampft. Die Gitterqualität ist so gut, dass sie nur von holografisch erzeugten Gittern übertroffen wird. Die Fertigung gleicht derjenigen einer CD-ROM, spielt sich allerdings wegen der erheblich kleineren Stückzahlen auf Manufakturniveau ab. Durch die Replikationstechnik ist man nicht auf den mechanischen Teilungsprozess bzw. die holografische Fertigung angewiesen, die beide einen erheblichen Zeit- und Kostenaufwand erfordern und mit hohen Ausfallrisiken behaftet sind.

Funktion

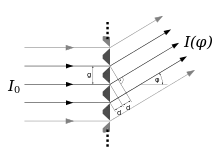
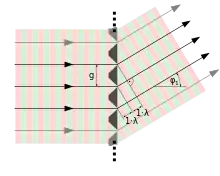
Beugung am Transmissionsgitter, g = Gitterkonstante, φ = Ablenkwinkel, d = Gangunterschied

Konstruktive Interferenz im ersten Hauptmaximum

Gittergleichung

Gitter erzeugen bei Bestrahlung mit Licht einer bestimmten Wellenlänge und Kohärenz eine Serie von Linien konstruktiver Interferenz. Bei Transmissionsgittern liegen diese beiderseits der Richtung des einfallenden Strahls („nullte Ordnung“). Die Winkel dieser Richtungen ergeben sich bei senkrechtem Einfall aus der Beziehung für den Gangunterschied $d\,$ :

d_{\text{n}}=n\cdot \lambda =g\cdot \sin(\varphi _{\text{n}}),\quad n\in \mathbb {Z}

(Hauptmaxima bei senkrechtem Einfall)

mit:

\lambda

= Wellenlänge,

g\,

= Gitterkonstante,

n\,

= Ordnung des Hauptmaximums,

\varphi _{\text{n}}

= Ablenkwinkel des Hauptmaximums,

Licht, das auf ein Beugungsgitter auftrifft, wird vergleichbar zum Doppelspaltexperiment gebeugt, die so entstehenden Elementarwellen interferieren und bilden so ein Gitterspektrum.

Für die Hauptmaxima gilt:

\lambda ={\frac {g\cdot \sin \varphi _{n}}{n}}

Bei $N$ an der Beugung beteiligten Gitterelementen ergeben sich zwischen zwei Hauptmaxima jeweils $N-1$ Minima bzw. Dunkelrichtungen. Deshalb werden die Hauptmaxima mit zunehmendem $N$ schärfer; die Nebenmaxima werden zwar zahlreicher, aber schwächer. Somit steigt das Auflösungsvermögen.

Bei nicht senkrechtem Einfall unter dem Winkel $\varphi _{i}$ zur Flächennormalen beträgt der Gangunterschied

d=g\cdot (\sin \varphi -\sin \varphi _{i}).

In der nullten Beugungsordnung (Einfallswinkel = Ausfallswinkel) ist $d=0,$ das Gitter reflektiert also auch wie ein Spiegel bzw. transmittiert wie eine Glasscheibe. Ein Blazegitter bevorzugt gezielt eine Beugungsordnung ≠ 0.

Intensitätsberechnung mit Fourier-Optik

Im Folgenden wird davon ausgegangen, dass das Gitter mit monochromatischem Licht bestrahlt wird. Um die genaue Intensitätsverteilung im Fernfeld des Gitters zu berechnen, nutzt man die Methoden der Fourieroptik. Die Blendenfunktion des Gitters setzt sich wie folgt zusammen:

Ein einzelner Spalt mit Breite b lässt sich mit der Rechteckfunktion $\operatorname {rect} _{b}(x)$ beschreiben.
Um zunächst unendlich viele Spalte mit gleichem Abstand a zu erhalten, faltet man den Einzelspalt mit einem Dirac-Kamm $\Delta _{a}(x)=\sum _{n\in \mathbb {Z} }\delta (x-n\,a)$ .
Die räumliche Begrenzung des Gitters wird durch die Multiplikation des gefalteten Dirac-Kamms mit einer Rechtecksfunktion $\operatorname {rect} _{B}(x)$ im x-Raum beschrieben. B ist dabei die Gesamtbreite des Gitters.

Die vollständige Blendenfunktion ist also:

A(x)=\operatorname {rect} _{B}(x)\cdot \left(\operatorname {rect} _{b}(x)*\left(\Delta _{a}(x)\right)\right)

Mit dem Kirchhoffschen Beugungsintegral lässt sich zeigen, dass das Beugungsmuster der Fouriertransformierten der Autokorrelation der Blendenfunktion entspricht.

Nach dem Baukastenprinzip und dem Faltungstheorem lässt sich die Fouriertransformierte der Blendenfunktion aus den Fouriertransformierten deren einzelner Komponenten zusammensetzen.

{\mathcal {F}}[\operatorname {rect} _{b}(x)](k)=b\cdot \operatorname {sinc} \left({\frac {b}{2}}k\right)=2{\frac {\sin \left({\frac {b}{2}}k\right)}{k}}

{\mathcal {F}}[\Delta _{a}(x))](k)={\frac {1}{a}}\Delta _{1/a}(k)

Die Fouriertransformierte des Delta-Kamms macht deutlich, dass ein kleinerer Abstand der Gitterspalte im x-Raum zu einem größeren Abstand der Minima und Maxima im k-Raum führt -- und umgekehrt.

Damit ergibt sich für die Intensitätsverteilung, als Quadrat der Amplitudenverteilung:

I(k)=I_{0}\cdot \left(\operatorname {sinc} \left({\frac {B}{2}}k\right)*\left(\operatorname {sinc} \left({\frac {b}{2}}k\right)\cdot {\frac {1}{a}}\Delta _{1/a}(k)\right)\right)^{2}

In vielen Fällen kann die endliche Breite des Gitters, die die Faltung im k-Raum bewirkt, vernachlässigt werden. Diese Methode ist jedoch derjenigen vorzuziehen, die die Begrenzung des Gitters mit einer endlichen Summe statt des unendlich langen Deltakamms beschreibt.

Bild und Beugungsbild eines Liniengitters
Liniengitter
Beugungsbild eines Liniengitters

Auflösungsvermögen

Das Auflösungsvermögen eines Gitters ergibt sich nach dem Rayleigh-Kriterium somit zu

{\frac {\lambda }{\Delta \lambda }}=nN

wobei $n$ die Ordnung des Maximums und $N$ die Anzahl ausgeleuchteter Linien ist.

Mehrfachspalt

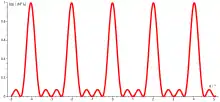
Intensitätsverteilung beim Vierfachspalt

Intensitätsverteilung als Heatmap hinter einem Mehrfachspalt

Fällt das Licht durch $N$ Spalte mit Abstand $g$ untereinander, spricht man von einem N-fach-Spalt oder Mehrfachspalt.

Die Hauptmaxima gibt es unter den gleichen Winkeln wie beim Gitter. Zwischen zwei Hauptmaxima liegen immer $N-1$ Nebenminima und $N-2$ Nebenmaxima. Deshalb werden die Hauptmaxima mit zunehmendem $N$ schärfer; die Nebenmaxima werden zwar zahlreicher, aber schwächer. Somit steigt das Auflösungsvermögen.

Die Intensitätsverteilung für schmale Spaltbreite ergibt sich zu[6]

I(\varphi )=I_{0}\cdot \left({\frac {\sin(N\,\pi \,{\frac {g}{\lambda }}\,\sin \varphi )}{\sin(\pi \,{\frac {g}{\lambda }}\sin \varphi )}}\right)^{2}

Bei Berücksichtigung der Spaltbreite $b$ ergänzt sich die Formel zu

I(\varphi )=I_{0}\cdot \left({\frac {\sin(\pi \,{\frac {b}{\lambda }}\,\sin \varphi )}{\pi \,{\frac {b}{\lambda }}\,\sin \varphi }}\,{\frac {\sin(N\,\pi \,{\frac {g}{\lambda }}\,\sin \varphi )}{\sin(\pi \,{\frac {g}{\lambda }}\sin \varphi )}}\right)^{2}

Herstellerspezifikationen

Hersteller geben für angebotene Gitter immer die mechanischen Abmessungen an, wodurch der nutzbare Strahldurchmesser festgelegt wird, sowie die Gitterkonstante, die allerdings typischerweise in „Linien/Millimeter“ angegeben wird. Bei Blaze-Gittern wird der Winkel angegeben sowie diejenige Wellenlänge, für die das Gitter durch Gitterkonstante und Blaze-Winkel optimiert ist. Bei holographischen Gittern wird dagegen immer ein ganzer Wellenlängenbereich angegeben, für den das Gitter ausgelegt ist.

Alltagsbeispiele

CDs weisen Spurabstände um 1,6 µm auf, so dass sie sich direkt als Gitter für den sichtbaren Teil des elektromagnetischen Spektrums (Wellenlängen 400–700 nm) eignen. Entsprechend sieht man ein deutlich aufgefächertes Farbspektrum, wenn man weißes Licht von einer CD reflektieren lässt. DVDs haben praktisch die gleiche Wirkung wie CDs.

CD mit Farbspektrum bei Weißlichtbestrahlung.
Eine CD zerlegt Licht in die einzelnen Farben/Wellenlängen.
Eine CD reflektiert den Lichtstrahl eines Laserpointers und zeigt mehrere Hauptmaxima.

Handydisplays und Gardinen erzeugen wegen der 2-dimensionalen Struktur komplexere Verteilungen der Intensitätsmaxima. Während Displays als Reflexionsgitter fungieren, wirken Gardinen wie ein Transmissionsgitter. Punktförmige Lichtquellen erzeugen bei Reflexion auf einem Handydisplay eine von der Pixelanordnung abhängige Verteilung der Intensitätsmaxima.

Beobachtbare Verteilung der Intensitätsmaxima bei einem Handydisplay.
Intensitätsmaxima beim Blick auf eine fast punktförmige Lichtquelle durch eine engmaschige Gardine.

Weblinks

Commons: Optische Gitter – Sammlung von Bildern, Videos und Audiodateien

The Optics of Spectroscopy – A Tutorial by J.M. Lerner and A. Thevenon

Einzelnachweise

Klaus Hentschel: Zum Zusammenspiel von Instrument, Experiment und Theorie. Rotverschiebung im Sonnenspektrum und verwandte spektrale Verschiebungseffekte von 1880 bis 1960. Kovac, Hamburg 1998, ISBN 978-3-86064-730-1, S. 84–95.
Deborah J. Warner: Lewis M. Rutherfurd: Pioneer Astronomical Photographer and Spectroscopist. In: Technology and Culture. Band 12, 1971, S. 190–216.
Deborah J. Warner in: The Michelson Era in American Science 1870–1930. American Institute of Physics, New York, S. 2–12.
George Sweetnam: The Command of Light: Rowland's School of Physics and the Spectrum. American Philosophical Society, Philadelphia 2000.
Klaus Hentschel: The discovery of the redshift of solar Fraunhofer lines by Rowland and Jewell in Baltimore around 1890. In: Historical Studies in the Physical and Biological Sciences. Band 23, Nr. 2. Berkeley 1993, S. 219–277 (uni-stuttgart.de [PDF]).
Lichtbeugung am Mehrfachspalt. Abgerufen am 26. Juli 2016.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Klaus Hentschel: Zum Zusammenspiel von Instrument, Experiment und Theorie. Rotverschiebung im Sonnenspektrum und verwandte spektrale Verschiebungseffekte von 1880 bis 1960. Kovac, Hamburg 1998, ISBN 978-3-86064-730-1, S. 84–95.

[2] Deborah J. Warner: Lewis M. Rutherfurd: Pioneer Astronomical Photographer and Spectroscopist. In: Technology and Culture. Band 12, 1971, S. 190–216.

[3] Deborah J. Warner in: The Michelson Era in American Science 1870–1930. American Institute of Physics, New York, S. 2–12.

[4] George Sweetnam: The Command of Light: Rowland's School of Physics and the Spectrum. American Philosophical Society, Philadelphia 2000.

[5] Klaus Hentschel: The discovery of the redshift of solar Fraunhofer lines by Rowland and Jewell in Baltimore around 1890. In: Historical Studies in the Physical and Biological Sciences. Band 23, Nr. 2. Berkeley 1993, S. 219–277 (uni-stuttgart.de [PDF]).

[6] Lichtbeugung am Mehrfachspalt. Abgerufen am 26. Juli 2016.