Babinetsches Prinzip

Das Babinet’sche Prinzip (auch Babinet’sches Theorem) ist ein Satz aus der Optik und besagt, dass die Beugungsbilder zweier zueinander komplementärer Blenden (beispielsweise Spaltblende und ein Draht gleicher Dicke) außerhalb des Bereiches, in den die geometrisch-optische Abbildung fällt (also die Abbildung ohne Beugungseffekte), gleich sind. Beispielsweise unterscheidet sich das Beugungsbild eines Einzelspalts kaum von dem eines Drahtes und das einer Kreisscheibe nicht von dem eines Loches in der Größe des Kreises.

Das Babinet’sche Prinzip gilt sowohl bei Fresnel- als auch bei Fraunhoferbeugung.

Der Name geht auf den französischen Physiker Jacques Babinet (1794–1872) zurück, der das Theorem 1837 aufstellte.

Erläuterung und Anwendung

Im einfachen Bild der geometrischen Optik breiten sich Lichtstrahlen geradlinig aus. Tatsächlich kann es jedoch durch Beugung zur Ablenkung des Lichtes kommen, beispielsweise wenn das Licht durch eine Blende fällt. An den Rändern der Blende werden die Lichtwellen gebeugt und Interferenz zwischen den gebeugten Lichtwellen führt zu Beugungserscheinungen, d. h., das Bild der Blende auf einem Schirm weicht von dem ab, was man für einen rein geometrisch-optischen Strahlenverlauf erwarten würde. Das Bild auf einem Schirm, das bei einem rein geometrisch-optischen Strahlenverlauf (also ohne Beugungseffekte) entstehen würde, soll im Folgenden mit „geometrisch-optischer Abbildung“ bezeichnet werden.

Das von Babinet 1837 aufgestellte Prinzip besagt nun, dass zueinander komplementäre Blenden – also Blenden, bei denen Öffnungen und undurchsichtige Bereiche vertauscht sind – außerhalb des Bereiches, den die geometrisch-optische Abbildung einnehmen würde, die gleichen Beugungserscheinungen erzeugen.

Komplementäre Blenden sind zum Beispiel ein Spalt und ein Draht, der genauso dick ist wie der Spalt breit, oder eine Kreisblende und ein Kreisplättchen gleichen Durchmessers. Das Babinet’sche Prinzip erlaubt es daher, die Beugung an einem undurchsichtigen Hindernis auf die an einer Öffnung desselben Umrisses zurückzuführen (siehe Korona – dort wird die Beugung an den Wassertropfen der Wolken auf die Beugung an einer Kreisblende zurückgeführt).

Anwendung in der Elektrodynamik

Analog zur Optik lässt sich das Babinet’sche Prinzip auch für die Elektrodynamik einsetzen, so dass sich nützliche Relationen ergeben. Beispielsweise können elektromagnetische Effekte durch Aperturen in leitenden Ebenen berechnet werden. Es reicht die Kenntnis der tangential zur Oberfläche liegenden elektrischen Felder aus, um die transmittierten Felder in der Apertur zu berechnen[1]. Zum Beispiel lässt sich damit das elektromagnetische Feld eines Loches in einer unendlich ausgedehnten, leitenden Oberfläche bestimmen, in der die Stromverteilung nicht berechnet werden kann. Das Loch wird gemäß dem Babinet’schen Prinzip also zur leitenden Oberfläche. Die Oberflächenströme müssen dann nur über das Loch berechnet werden und die Rücktransformation bietet schließlich das Ergebnis für ein Loch in einer unendlich großen, leitenden Fläche.

Herleitung

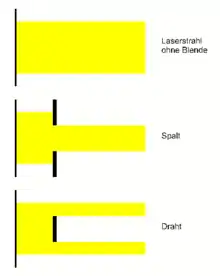
Geometrisch-optische Strahlausbreitung (d. h. ohne Beugung) durch komplementäre Blenden (schematisch)

Fällt ein Lichtstrahl auf einen Schirm, erzeugt er dort einen hellen Bereich. Wenn zwischen der Lichtquelle und dem Schirm kein Hindernis liegt, breitet sich der Strahl geradlinig – also ungebeugt – aus. Der helle Bereich auf dem Schirm entspricht daher der geometrisch-optischen Abbildung (Abbildung rechts; oben). Die Verteilung von Helligkeit und Dunkelheit auf dem Schirm entspricht einer Verteilung der Amplitude der Lichtwelle. Die Amplitude soll hier mit $E_{0}(x)$ bezeichnet werden. Im hellen Bereich ist die Amplitude groß, außerhalb des hellen Bereiches ist der Schirm dunkel, dort ist die Amplitude also null. Nun sollen zwei komplementäre Blenden nacheinander in den Strahl eingebracht werden (beide Blenden zusammen sollen den Strahl vollständig verdecken), wie in der Abbildung rechts, Mitte und unten, ohne Berücksichtigung von Beugungseffekten dargestellt.

Sowohl die Lochblende als auch das undurchsichtige Hindernis erzeugen aber natürlich ein Beugungsbild. Für diese Beugungsbilder von Lochblende und Hindernis kann die auf den Schirm fallende Amplitude jeweils in einen geometrischen und einen Beugungsanteil zerlegt werden:

(1)

E_{\text{loch}}(x)=E_{\text{lochgeo}}(x)+E_{\text{lochbeug}}(x)

(2)

E_{\text{hind}}(x)=E_{\text{hindgeo}}(x)+E_{\text{hindbeug}}(x)

E(x)

= Amplitudenverteilung auf dem Schirm;

x\,

= Koordinate längs des Schirms; loch = Lochblende; hind = zur Lochblende komplementäres Hindernis; geo = geometrischer Anteil; beug = Beugungsanteil

Da die eine Blende jeweils das Licht durchlässt, welches die andere ausschneidet, müssen beide Beugungsbilder zusammen wieder die geometrisch-optische Abbildung der Lichtquelle ohne Blende ergeben. Die Summe der Gesamtamplituden hinter der Lochblende und dem Hindernis $E_{\text{loch}}(x)+E_{\text{hind}}(x)$ muss also gleich $E_{0}(x)$ sein:

(3)

E_{\text{loch}}(x)+E_{\text{hind}}(x)=E_{0}(x)

Die Summe der geometrischen Anteile beider Amplitudenverteilungen $E_{\text{lochgeo}}(x)+E_{\text{hindgeo}}(x)$ muss gleich dem geometrischen Anteil des Bildes ohne Blende sein – sie muss also ebenfalls gleich $E_{0}(x)$ sein, da es ohne Blende nur den geometrischen Anteil gibt:

(4)

E_{\text{lochgeo}}(x)+E_{\text{hindgeo}}(x)=E_{0}(x)

Setzt man nun Gl. (1) und (2) in Gl. (3) ein, erhält man:

(5)

E_{\text{loch}}(x)+E_{\text{hind}}(x)=E_{\text{lochgeo}}(x)+E_{\text{lochbeug}}(x)+E_{\text{hindgeo}}(x)+E_{\text{hindbeug}}(x)=E_{0}(x)

Mit Gl. (4) ergibt sich:

(6)

E_{0}(x)+E_{\text{lochbeug}}(x)+E_{\text{hindbeug}}(x)=E_{0}(x)

und damit:

(7)

E_{\text{lochbeug}}=-E_{\text{hindbeug}}

Die Anteile der Amplituden, die auf die Beugung entfallen, sind für Lochblende und Hindernis also gleich groß, haben aber entgegengesetztes Vorzeichen – die Amplitudenverteilung der Lochblende ist demnach außerhalb der geometrisch-optischen Abbildung entgegengesetzt zu derjenigen des komplementären Hindernisses: Wo die Lochblende eine negative Amplitude erzeugt, ergibt das Hindernis eine betragsmäßig gleich große positive Amplitude und umgekehrt. Überlagern sich zwei Amplituden, die gleich groß sind, aber entgegengesetztes Vorzeichen haben, ist die Amplitude der Gesamtwelle null, es kommt zur Auslöschung. Überlagert man also die Amplitudenverteilungen beider komplementärer Blenden, erhält man (außerhalb der geometrisch-optischen Abbildung) Auslöschung, und damit Dunkelheit, wie man es für den Fall erwartet, in dem es überhaupt keine Blenden gibt. Die Überlagerung der Amplituden hinter den beiden komplementären Blenden ergibt also die Amplitudenverteilung der Anordnung ohne Blenden.

Für die Wahrnehmung der Beugungsbilder ist nun aber nicht die Amplitude entscheidend, sondern die Intensität. Die Intensität des Lichtes ist proportional zum Quadrat der Amplitude – für die Intensität der Beugungsmaxima ist es also gleichgültig, ob die Amplitude positiv oder negativ ist, es kommt nur auf ihre betragsmäßige Größe an. Erzeugt die Lochblende an einer Stelle eine große positive Amplitude, sorgt die komplementäre Blende an derselben Stelle für eine betragsmäßig gleich große negative Amplitude – und beide haben dieselbe Intensität zur Folge. Aus diesem Grund sind die Beugungsbilder von Lochblende und Hindernis außerhalb der geometrisch-optischen Abbildung gleich.

Fraunhofer-Beugung

Beugungsbilder einer Stecknadel und eines Spaltes zwischen zwei Rasierklingen, dessen Breite mithilfe der Stecknadel erzeugt wurde. Beleuchtet wurde mit einem roten Laserpointer. Wegen der Ungenauigkeit, mit der die Breite von Spalt und Nadel (nicht) in Übereinstimmung gebracht werden konnten, weichen die Positionen der Maxima voneinander ab.

Das Babinet’sche Theorem gilt sowohl für Fresnel- als auch bei Fraunhoferbeugung. Bei der Fraunhofer-Beugung befindet sich die Lichtquelle in unendlich großer Entfernung, d. h., die Lichtquelle muss hinreichend klein und der Abstand zwischen ihr und dem Beobachtungsschirm hinreichend groß sein (bzw. Lichtquelle und Schirm müssen durch Linsen in unendliche Entfernung „gerückt“ werden). Im Fall einer annähernd punktförmigen Lichtquelle wird auch der Bereich der geometrisch-optischen Abbildung sehr klein und spielt im Beugungsbild kaum eine Rolle. Damit sehen bei der Fraunhofer-Beugung die Beugungsbilder der komplementären Blenden insgesamt (fast) gleich aus. (Daher ist es gerechtfertigt, die bei der Entstehung der Korona maßgebliche Beugung an Wassertropfen durch eine Beugung an Kreisblenden zu ersetzen.)

Erweiterung auf vektorielle Feldgrößen

Die oben beschriebenen Beugungserscheinungen beziehen sich auf die Beträge der elektrischen Felder bzw. die Intensitätsverteilung der gebeugten elektromagnetischen Strahlung. Sie werden (wie oben durchgeführt) im Rahmen der Näherungen des Kirchhoffschen Beugungsintegrals für skalare Feldgrößen hergeleitet. Will man Aussagen über die komplexwertigen elektrischen und magnetischen Felder und die Polarisationseigenschaften treffen, so beschränkt man sich in der Regel auf den Fall von Blenden aus unendlich dünnen und perfekt elektrisch leitenden Materialien. Bei den senkrecht auf die Blenden einfallenden elektrischen und magnetischen Feldanteilen ist zu beachten, dass beim Wechsel zwischen den komplementären Blenden eine 90°-Rotation der Feldvektoren um die Flächennormale vorzunehmen ist[2][3][4]. Hinsichtlich des Drehsinns und anderer Details sei auf die angegebenen Referenzen und das Lehrbuch Classical Electrodynamics von J. D. Jackson verwiesen. Elektrische Dipolmomente der einen Blende werden hierbei zu magnetischen Dipolmomenten der komplementären Blende und umgekehrt.

Literatur

Bergmann/Schaefer: Lehrbuch der Experimentalphysik, Band 3: Optik. 10. Aufl., 2004, Walter de Gruyter, Berlin, S. 368

Weblinks

Einzelnachweise

Leugner, Dietmar.: Berechnung der Elektromagnetischen Einkopplung durch Aperturen mit analytischen Verfahren und der Momentenmethode. Als Ms. gedr Auflage. VDI-Verl, Düsseldorf 2004, ISBN 3-18-336021-7.
F. Falcone et al., Babinet principle applied to the design of metasurfaces and metamaterials, Physical Review Letters 93, 197401 (2004), DOI: 10.1103/PhysRevLett.93.197401
A. Blitzer et al., Terahertz near-field microscopy of complementary planar metamaterials: Babinet's principle, Optics Express 19, 2537–2545 (2011), DOI: 10.1364/OE.19.002537
D. Lee et al., Light scattering of rectangular slot antennas: parallel magnetic vector vs perpendicular electric vector, Scientific Reports 6, 18935 (2016), DOI: 10.1038/srep18935

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Leugner, Dietmar.: Berechnung der Elektromagnetischen Einkopplung durch Aperturen mit analytischen Verfahren und der Momentenmethode. Als Ms. gedr Auflage. VDI-Verl, Düsseldorf 2004, ISBN 3-18-336021-7.

[2] F. Falcone et al., Babinet principle applied to the design of metasurfaces and metamaterials, Physical Review Letters 93, 197401 (2004), DOI: 10.1103/PhysRevLett.93.197401

[3] A. Blitzer et al., Terahertz near-field microscopy of complementary planar metamaterials: Babinet's principle, Optics Express 19, 2537–2545 (2011), DOI: 10.1364/OE.19.002537

[4] D. Lee et al., Light scattering of rectangular slot antennas: parallel magnetic vector vs perpendicular electric vector, Scientific Reports 6, 18935 (2016), DOI: 10.1038/srep18935