Prisma (Optik)
Unter einem Prisma wird in der Optik ein Bauelement in Form des geometrischen Körpers Prisma verstanden, das für unterschiedliche optische Effekte eingesetzt wird, z. B. als dispersives (Licht nach Wellenlängen auffächerndes) Element oder zur Umlenkung eines Lichtstrahls. Bei der Form handelt es sich häufig um ein gerades Prisma mit einem Dreieck als Grundfläche. Die optischen Eigenschaften eines Prismas hängen im Wesentlichen ab von den Dreieckswinkeln bzw. der Lage der optisch wirksamen Prismenflächen zueinander und vom Brechungsindex des Werkstoffes (z. B. Glas oder transparenter Kunststoff).


Anwendungen
Die Hauptanwendungen des Prismas beruhen typischerweise entweder auf seiner Eigenschaft, Licht wellenlängenabhängig zu brechen – das ist dann »Dispersion« – oder darauf, Lichtstrahlen durch Reflexion an einer oder an mehreren Flächen umzulenken, etwa im Sucher einer Spiegelreflexkamera.[1] Dabei kommen sowohl Totalreflexion als auch gerichtete Reflexion an mit Metall beschichteten Prismenflächen zum Einsatz.
Dispersionsprisma

Wird das lichtwellenlängenabhängige (dispersive) Verhalten des Materials eines Prismas ausgenutzt, wird es als Dispersionsprisma bezeichnet. Diese werden z. B. in Prismenspektrometern eingesetzt. Dabei fällt das Licht schräg auf eine Seitenfläche des Prismas, im einfachsten Fall auf ein Prisma in Form eines gleichschenkligen Dreiecks. Durch den schrägen (genauer nicht-senkrechten) Einfall und den für jede Wellenlänge spezifischen Brechungsindex werden die verschiedenen Wellenlängen in einem jeweils anderen Winkel an der Grenzfläche gebrochen. Dieser Effekt tritt erneut an der Austrittsfläche des Prismas auf, wo der aufgespaltene Lichtstrahl in unterschiedlichen Winkeln auftrifft, wodurch sich die Brechung und damit die Aufspaltung noch weiter verstärken. Die gemeinsame Kante der beiden beteiligten Flächen (im Diagramm oben) heißt die ablenkende oder brechende Kante, bezüglich der das Licht in die Gegenrichtung abgelenkt wird.
Umgekehrt kann dieser Effekt unter Einsatz von monochromatischem Licht bekannter Wellenlänge zur Bestimmung des Brechungsindexes (der Dispersion) eingesetzt werden. Dabei wird ausgenutzt, dass die Ablenkung des gebrochenen Lichtes bei einem symmetrischen Durchgang minimal ist. Der Brechungsindex lässt sich dann wie folgt bestimmen:
mit:
- n = Brechungsindex des Materials für das verwendete monochromatische Licht
- = minimaler Ablenkungswinkel
- = Winkel zwischen den beiden brechenden Kanten
Reflexionsprisma
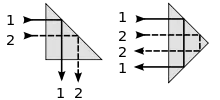
links: Eine einmalige Umlenkung spiegelt das Bild.
rechts: Eine zweimalige Umlenkung kehrt Bild um.
Prismen, deren Anwendung auf dem Effekt der Totalreflexion basiert, werden zur verlustarmen Umlenkung von Licht genutzt. Sie werden Umlenkprisma bzw. Reflexionsprisma genannt. Das einfachste Beispiel für ein Umlenkprisma ist ein Prisma mit der Grundfläche eines gleichschenkligen, rechtwinkligen Dreiecks. Hierbei bilden die beiden senkrecht aufeinanderstehenden Flächen die Ein- und Austrittsflächen. Die dritte Fläche dient als Reflexion- bzw. Umlenkfläche, an der einfallendes Licht, das unter einem Winkel, der größer ist als der Grenzwinkel der Totalreflexion, totalreflektiert wird, das heißt ohne Reflexionsverluste. Um einen möglichst hohen Transmissionsgrad für den gesamten Strahlengang zu erreichen, wird das Licht senkrecht auf die Eintrittsfläche geführt. In diesem Fall ist der Transmissionsgrad für unpolarisiertes Licht maximal und man vermeidet eine Aufspaltung des Lichts in Abhängigkeit von der Wellenlänge oder der Polarisation, denn senkrecht auf eine Grenzfläche einfallendes Licht wird nicht gebrochen. Einfache Umlenkprismen werden in optischen Instrumenten gezielt zur Lichtführung eingesetzt, beispielsweise für die verlustarme Umlenkung eines Laserstrahls in FTIR-Spektrometern.
Kombiniert man zwei Umlenkprismen, kann die Spiegelbildwirkung einer einmaligen Reflexion umgekehrt werden und ein Bild wird auf diese Weise aufgerichtet. Solche auch als Umkehrprisma bezeichneten Systeme werden beispielsweise in Prismenferngläsern eingesetzt. Auch das Pentaprisma, mit einem Fünfeck als Grundfläche, ist im Prinzip eine solche Kombination aus zwei dreieckigen Umlenkprismen. Es wird zur 90°-Umlenkung benutzt, wobei das Bild seitenrichtig bleibt. Beim Pentadachkantprisma ist eine der vier spiegelnden Flächen durch zwei zueinander rechtwinklige Flächen ersetzt, wodurch das Bild gespiegelt wird. Es wird in Spiegelreflexkameras angewendet, um das durch deren Spiegel verkehrte Bild zu korrigieren.
Die Vorteile eines totalreflekierenden Umlenkprismas gegenüber einer Spiegelanordnung sind unter anderem die Lageunveränderlichkeit der spiegelnden Flächen, die kompakte Bauweise und der höhere Transmissionsgrad bei mehreren Reflexionen. So ist der Transmissionsgrad eines Pentaprismas deutlich höher als bei einem Pentaspiegel, denn beim Prisma treten hier nur Reflexionsverluste beim Ein- und Austritt auf (bei Glas jeweils ca. 4 %), die mit entsprechenden Antireflexionsschichten nochmal gesenkt werden können. Die Reflexionsverluste bei einer metallischen Fläche betragen hingegen ca. 6 bis 10 %, was schon bei zwei Reflexionen zu deutlich geringeren Transmissionsgraden der Anordnung führt.
Polarisationsprisma
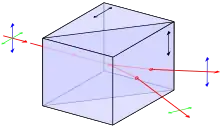
Polarisationsprismen eignen sich dafür, Licht in Anteile unterschiedlicher Polarisation zu trennen. Ihre Funktionsweise beruht auf der Doppelbrechungseigenschaft des verwendeten Prismenmaterials. Anders als bei Dispersionsprismen wird nicht die Abhängigkeit des Brechungsindex von der Wellenlänge, sondern seine Abhängigkeit von der Polarisation des Lichtes ausgenutzt. Das heißt, einfallendes Licht wird in Abhängigkeit von der Polarisation unterschiedlich stark gebrochen, und die Strahlanteile divergieren im Prisma. Primär bestimmt dabei nicht die Lage der Grenzflächen zueinander, sondern die Lage der Grenzflächen zur optischen Achse des genutzten doppelbrechenden Materials die Eigenschaften des Polarisationsprismas. Zur Verstärkung dieser Aufspaltung oder Auswahl der Polarisation wird in der Regel eine Kombination aus zwei unterschiedlich orientierten Teilprismen angewendet, die häufig zusammengeklebt sind, wobei der Kleber (wie Kanadabalsam) zudem einen optischen Zweck hat. Häufig werden sie an einer schräg zur ursprünglichen Strahlrichtung verlaufenden Fläche zusammengefügt. Durch den schrägen Einfall und den unterschiedlichen Brechindex kann so beispielsweise über Totalreflexion eine Auswahl realisiert werden.
Eines der bekanntesten Polarisationsprismen ist das Nicolsche Prisma. Varianten sind das Glan-Thompson-Prisma und das Glan-Taylor-Prisma.
Prismendioptrie
Als Maß für die Stärke eines Prismas wurde früher die Maßeinheit Prismendioptrie verwendet (Einheitenzeichen pdptr) verwendet. Sie ist über den Ablenkungswinkel α definiert mit .
Heute taucht sie noch vereinzelt in der Augenheilkunde auf. Sie wird definiert durch den Grad der Ablenkung eines Lichtstrahls gemessen in Zentimeter, in einem Meter Entfernung (cm/m). Demnach ist 1 pdptr die Ablenkung eines Lichtstrahls um 1 cm in 1 m Entfernung.[2] Zur Beschreibung prismatischer Wirkungen sollte nur noch die Einheit Zentimeter pro Meter (cm/m) verwendet werden (1 pdptr = 1 cm/m).
Weblinks
Einzelnachweise
- Dietrich Kühlke: Optik. Grundlagen und Anwendungen. 2., überarbeitete und erweiterte Auflage. Harri Deutsch, Frankfurt am Main 2004, ISBN 3-8171-1741-8, S. 126–131.
- Theodor Axenfeld (Begründer), Hans Pau (Hrsg.): Lehrbuch und Atlas der Augenheilkunde. 12., völlig neu bearbeitete Auflage. Gustav Fischer, Stuttgart u. a. 1980, ISBN 3-437-00255-4.