Unmögliche Figur
Unmögliche Figuren sind grafisch zweidimensionale, vorgeblich dreidimensionale Konstrukte in der Kunst, die körperhaft nicht existieren können. Bei den Figuren handelt es sich entweder um Paradoxa oder um optische Täuschungen. Als erstes wurden sie von Oscar Reutersvärd entwickelt; der niederländische Grafiker M. C. Escher hat im 20. Jahrhundert zahlreiche solcher unmöglichen Figuren geschaffen.
Die Lösung des Widerspruches ergibt sich aus der flächenhaften Darstellung in zwei Dimensionen und der Sinneswahrnehmung als dreidimensionale Gebilde.
Beispiele unmöglicher Figuren
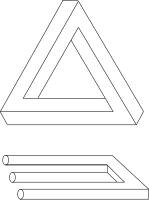 Penrose-Dreieck (Tribar) und Unmöglicher Dreizack (Blivet)
Penrose-Dreieck (Tribar) und Unmöglicher Dreizack (Blivet)
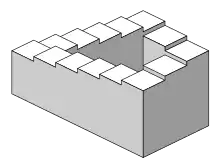 Die Penrose-Treppe
Die Penrose-Treppe
Im Artikel Penrose-Dreieck finden sich Bilder von Skulpturen, die aus einer Perspektive betrachtet/abgebildet ungefähr wie ein Penrose-Dreieck erscheinen.
Unmögliche Figuren von Escher
Eschers Bilder sind keine optischen Täuschungen, für die sie oft gehalten werden. In seinen Bildern vermischt Escher Ansichten von rechts und von links, bzw. von oben und von unten, wodurch ein ebenes Bild entsteht, das wie das Bild eines dreidimensionalen Gegenstandes aussieht, es aber nicht sein kann. Da jedoch das menschliche Auge es so wahrnimmt, entstehen Bilder von unmöglichen Figuren.[1]
Entstehung eines optischen Trugschlusses am Beispiel der Penrose-Treppe
Die linke und die rechte Teilansicht der Penrose-Treppe sind einzeln real wahrnehmbar. Fügt man beide Teilansichten zur vollständigen Penrose-Treppe zusammen, so entsteht eine unmögliche Figur.
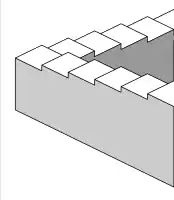 Linker Teil der Penrose-Treppe
Linker Teil der Penrose-Treppe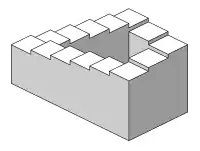 Penrose-Treppe
Penrose-Treppe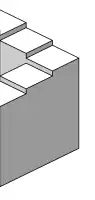 Rechter Teil der Penrose-Treppe
Rechter Teil der Penrose-Treppe
Siehe auch
Literatur
- M. C. Escher: Grafiek en Tekeningen. Koninklijke Erven J.J. van Tijl, Zwolle 1959. IX Konfliekt
- Bruno Ernst: Abenteuer mit unmöglichen Figuren. Taco, Berlin 1987. ISBN 3-89268-012-4
Weblinks
Einzelnachweise
- Unmögliche Figuren (Escher) aus mathe-werkstatt.de, abgerufen am 8. Mai 2021