Mondtäuschung
Die Mondtäuschung ist eine optische Täuschung, durch welche der Mond und die Sonne in Horizontnähe größer erscheinen als bei höherem Stand am Firmament. Für diesen insbesondere beim Aufgang des Vollmondes bekannten Effekt gibt es keine physikalische oder astronomische Erklärung. Die Ursache dieses wahrnehmungspsychologischen Phänomens ist nicht endgültig geklärt.[1]

In Relation zum Sehwinkel des Daumens einer ausgestreckten Hand entspricht der Sehwinkel des Mondes unabhängig vom Stand tatsächlich der auf nebenstehendem Bild rechts abgebildeten kleinsten Mondscheibe, auch wenn die meisten Menschen aus der Erinnerung eher auf die Größe der links abgebildeten größten Mondscheibe tippen würden. Der scheinbare Durchmesser des Mondes (siehe auch Winkelschätzung) beträgt 31 Bogenminuten, also ungefähr 0,5 Grad. Drei bis vier Mondscheiben nebeneinander gelegt erscheinen unter dem gleichen Sehwinkel wie die Breite des ausgestreckten Daumens, die je nach Daumenbreite und Länge des Arms bei ungefähr 1,5 bis 2 Grad liegt.

Geschichte
Erste Hinweise auf das Phänomen der Mondtäuschung finden sich auf Tontafeln aus den königlichen Bibliotheken von Niniveh und Babylon (6. Jahrhundert v. Chr.). Ptolemäus (ca. 150 n. Chr.) vermutete fälschlicherweise vergrößernde Eigenschaften der Atmosphäre. Alhazen (Abu Ali al-Hasan ibn al-Haitham, 965 bis ca. 1040) stellte fest, dass der Mond sowohl am Horizont als auch im Zenit die gleiche Größe hat, und schrieb bereits vom abgeflachten Firmament (siehe unten) als Ursache der Wahrnehmungstäuschung. Auch Leonardo da Vinci, Johannes Kepler und René Descartes beschäftigten sich mit der Mondtäuschung. Seit über 100 Jahren wird diese optische Täuschung von der wissenschaftlichen Wahrnehmungspsychologie untersucht. Dennoch ist das Phänomen noch immer nicht eindeutig geklärt, es bleiben Widersprüche bei den unterschiedlichen Erklärungsansätzen. Die derzeit anerkanntesten und von vielen Experimenten untermauerten Erklärungen sind die der falsch eingeschätzten Entfernung mit dem abgeflachten Firmament und das Prinzip der Vergleichsobjekte.
Erklärungsansätze
Oft wird fälschlicherweise vermutet, dass die Täuschung eine Folge der „Rötung“ sei – durch die Rayleigh-Streuung wird viel mehr blaues als rotes Licht an den Atomen und Molekülen der Erdatmosphäre aus dem zum Beobachter gerichteten Strahlenbündel von Sonne und Mond in Horizontnähe herausgestreut, so dass ein größerer Anteil an rotem Licht zum Auge des Beobachters gelangt. Auch ist sie keine Folge der Refraktion. Eine durch Refraktion oder Rötung erfolgte Größenveränderung müsste auch auf einer Fotografie zu sehen sein, was aber nicht der Fall ist.
Sehwinkel und Größenwahrnehmung
Wesentlich für die korrekte Größenwahrnehmung eines Gegenstandes ist die ebenso korrekte Information über dessen tatsächliche Entfernung zum Beobachter. Aus der Größe der Abbildung (dem Sehwinkel) eines Objekts auf der Netzhaut und dem gleichzeitig vorhandenen Wissen über dessen Entfernung „errechnet“ das menschliche Gehirn unbewusst die tatsächliche Größe des Objekts (Emmertsches Gesetz), indem es auf die Erfahrung zurückgreift, dass ein naher Gegenstand ein größeres Abbild auf der Netzhaut hervorruft als derselbe, weiter entfernte Gegenstand. Da die Entfernung des Mondes zur Erde sich während der Bewegung auf seiner elliptischen Umlaufbahn nur um etwa 10 % verändert und innerhalb einer Nacht somit unter einem Prozent bleibt, muss es sich bei der vermeintlichen erheblichen Größenzunahme des Mondes bei Auf- und Untergang um eine Täuschung handeln.
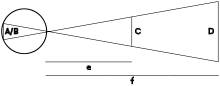
Wahrnehmungstäuschungen bezüglich der Größe entstehen meist dann, wenn eine unbewusste falsche Einschätzung der Entfernung vorliegt: Ein Gegenstand (D) in fester Entfernung (f), der ein Abbild in der Größe (A) auf der Netzhaut erzeugt, und dessen Entfernung fälschlicherweise unterschätzt (e) wird, wird als kleiner beziehungsweise als gerade so groß (C) wahrgenommen, wie er sein müsste, um in dieser unterschätzten geringeren Entfernung die Größe (A) auf der Netzhaut zu erzeugen (siehe die Skizze oben). Ein Beispiel dafür ist der hoch stehende Mond oder auch der sogenannte „Spielzeugautoeffekt“: Wenn man von einem hohen Turm hinunterschaut, wird mangels Erfahrung die Entfernung unterschätzt und die Autos unten werden kleiner, wie Spielzeugautos, wahrgenommen.
Umgekehrt: Ein Gegenstand (C) in fester Entfernung (e), der ein Abbild in der Größe (B) auf der Netzhaut erzeugt, und dessen Entfernung fälschlicherweise überschätzt (f) wird, wird als größer beziehungsweise als gerade so groß (D) wahrgenommen, wie er sein müsste, um in dieser überschätzten größeren Entfernung die Größe (B) auf der Netzhaut zu erzeugen (siehe Skizze). Ein Beispiel dafür ist der Mond in Horizontnähe, die „Mondtäuschung“: Da zwischen Mond am Horizont und Betrachter viel mehr Gegenstände (Bäume, Häuser, Hügel etc. – mehr „Tiefeninformation“) liegen als zwischen Mond oben am Himmel und Betrachter, wird die Entfernung fälschlicherweise als größer eingeschätzt, bei größerer Entfernung und gleich großer Abbildung auf der Netzhaut müsste der Gegenstand aber größer sein, und somit wird der Mond oder auch die Sonne am Horizont auch größer wahrgenommen.
Tiefeninformation
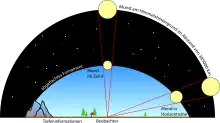
Durch die Tiefeninformation (Bäume, Häuser etc.) bei waagrechter Blickweise zum Horizont und die fehlende Tiefeninformation beim Blick nach oben erhält das Firmament, auf dem Mond, Sonne und auch die Sterne scheinbar stehen, eine abgeflachte Form. Bei real gleich großer Abbildung auf der Netzhaut des Auges wird der scheinbar weiter entfernte Mond am Horizont größer wahrgenommen und der scheinbar weniger weit entfernte Mond bei höherem Stand kleiner.
Wegen der abgeflachten Form des Firmaments werden auch die einzelnen Sterne eines Sternbildes (zum Beispiel des Sternbilds Schwan) als weiter auseinander stehend wahrgenommen, das ganze Sternbild erscheint also größer, wenn es in Horizontnähe steht, als wenn es im Zenit steht: Und es wird kontinuierlich kleiner, wenn es sich beispielsweise im Verlauf einer Nacht vom Ost-Horizont her kommend dem Zenit annähert. Es gibt diese kontinuierliche und lineare Größenveränderung in Abhängigkeit von der Position am Himmel zwar bei den Sternbildern, aber nicht so eindeutig beim Mond oder der Sonne. Die scheinbare Größenveränderung von Sonne und Mond fällt – im Gegensatz zur Größenwahrnehmung bei den Sternbildern – erst in Horizontnähe auf.
Für das Erklärungsprinzip des abgeflachten Firmamentes spricht, dass nur damit auch die scheinbare kontinuierliche Größenveränderung der Sternbilder erklärt werden kann, während das Prinzip der Vergleichsobjekte (siehe unten) besser erklären kann, warum eine Größenveränderung von Sonne und Mond erst in Horizontnähe wahrgenommen wird.
Vergleichsobjekte


Zur scheinbaren Größenveränderung trägt auch das Prinzip der Vergleichsobjekte bei: Weil der Mond am Horizont im Vergleich mit durch die große Entfernung klein wirkenden Objekten, etwa in weiter Ferne stehenden Bäumen oder Häusern, gesehen wird, wirkt er dort größer, als wenn er hoch stehend im Vergleich mit dem großen Firmament gesehen wird oder auch im Vergleich zu in unmittelbarer Nähe befindlichen vergleichsweise groß wirkenden Baumkronen.
Allerdings wird der Mond auch dann am Horizont sehr groß wahrgenommen, wenn es keine kleineren Vergleichsobjekte gibt, z. B. in der Wüste oder am Meer. Der Horizont ist dort wegen der unverstellten Sicht sehr weit entfernt einzusehen, und es gibt viel perspektivische Tiefeninformation. Dies widerspricht der ausschließlichen Erklärung des Phänomens durch kleinere Vergleichsobjekte und ist eher als Beleg für das Prinzip der überschätzten Entfernung zu werten.
Dazu kommt noch folgendes Paradoxon: Der wegen des scheinbar größeren Abstands „am Horizont“ größer wahrgenommene Mond scheint wegen seiner ungewöhnlichen Größe wieder näher zu sein. Diese Paradoxie könnte sich so auflösen: Es vermischen sich hier die Täuschungen nach zwei Prinzipien der Entfernungswahrnehmung:
- mehr Dinge (Tiefeninformation und Perspektive) dazwischen bedeuten eine größere Entfernung,
- ein größeres Objekt ist näher.
Variabler Wahrnehmungsbereich
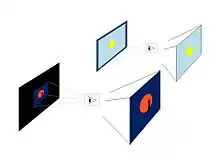
In dieser Hypothese wird das visuelle System einem Datenkanal gleichgesetzt. Während das Bild auf der Netzhaut sehr viel Information enthalten kann, stellt die weitere neuronale Verarbeitung des Bilds zur Wahrnehmung einen Engpass dar: Pro Sekunde kann nur eine bestimmte Informationsmenge übertragen und verarbeitet, also nur eine begrenzte Zahl von Bildelementen identifiziert werden. Mit diesen kann man zwar wahlweise einen größeren oder kleineren Bildausschnitt darstellen bzw. wahrnehmen, aber ein kleinerer Ausschnitt zeigt mehr Detailinformation, da die Bildelemente dann dichter gepackt sind. Ein größerer Ausschnitt hat wiederum den Vorteil des Überblicks. Nimmt man noch an, dass der jeweils gewählte Bildausschnitt – ob groß oder klein (im Bild links) – auf eine Art inneren Monitor oder einen Speicher konstanter Größe im visuellen System projiziert wird (rechts), dann stellt sich die Mondtäuschung so dar:
Aufgrund der begrenzten Kanalkapazität wird nur ein Ausschnitt des Retinabilds zur Wahrnehmung verarbeitet. Ist der erfasste Bereich klein, dann vermitteln die identifizierten Bildelemente eine hohe Detailauflösung. Ein einzelnes Objekt macht einen großen Anteil an diesem Bereich aus und erscheint deshalb groß, auch der Mond. Bei einem großen Wahrnehmungswinkel ist die Auflösung entsprechend geringer, außerdem wirkt alles – da auf dieselbe Fläche projiziert – entsprechend kleiner. Der immer gleich große „innere Monitor“ steht dabei bildhaft für die Vorstellung, dass das visuelle System bei der Betrachtung eines großen wie auch eines kleinen Bereichs immer seine volle Datenkapazität einsetzt, um in beiden Fällen eine vergleichbare Anzahl charakteristischer Details zu erfassen.
Dass die Größenwahrnehmung mit der Auflösung von Details im Zusammenhang stehe, vermutete schon Goüye (1700).[3] Er vergleicht den Mond hinter Bäumen und Zweigen mit einer Säule, die dicker erscheine, wenn sie Rillen habe. Lühr (1898)[4] bzw. Cornish (1937)[5] äußerten den Gedanken, dass sich die visuelle Wahrnehmung auf einen begrenzten, aber in seiner Größe veränderlichen Bereich konzentriere. Während Lühr tief bzw. hoch am Himmel stehende Sternbilder diskutiert, begründet Cornish eine unterschiedliche Größenwahrnehmung der Sonne am Horizont mit dessen Form (flach bzw. hoch).
Experimente zur Messung der wahrgenommenen Größe einer hellen Kreisscheibe wurden von Erna Schur[6] bzw. von Lloyd Kaufman und Irvin Rock[7] durchgeführt. Während Schur eine starke Vergrößerung in der Wahrnehmung in horizontaler Blickrichtung gegenüber der vertikalen auch bei nahen terrestrischen Stimuli fand, berichten Kaufmann und Rock, dass in vertikaler Blickrichtung eine virtuelle Kreisscheibe dann größer erschien, wenn der natürliche Horizont über einen Spiegel in die Sichtlinie eingeblendet wurde.
In evolutionären Zeiträumen hat das Gehirn gelernt, am Horizont ganz automatisch einen kleineren Bereich ins Auge zu fassen, um möglichst frühzeitig Strukturen zu identifizieren, die Nahrung oder Schutz versprachen oder auch Konkurrenz und Fressfeinde verrieten. Ein weiträumiges Erfassen – unter Verzicht auf hohe Auflösung – wurde dann gewählt, wenn es z. B. um die Beurteilung des Wetters oder das Auffinden eines Vogelschwarms irgendwo am weiten Himmel ging.
Einen ungewöhnlich großen Himmelskörper beobachtet man am Horizont, wenn dieser als dominierende Lichtquelle die Details in seinem Bereich scharf und kontrastreich hervorhebt. Das Bestreben des visuellen Systems, kleine Objekte wegen der dort herrschenden guten Sichtbedingungen auch besonders gut aufzulösen, bewirkt die Einstellung eines entsprechend kleinen Wahrnehmungswinkels, was dann auch den Mond (oder die Sonne) automatisch mit vergrößert. Bei den irdischen Objekten fällt der Vergrößerungseffekt nicht so auf, da man diese ständig aus unterschiedlichen Entfernungen und damit auch unterschiedlich groß sieht, während bei Himmelskörpern mit ihrer immer gleichen Ausdehnung eine scheinbare Größenänderung stärker ins Auge sticht.
Tatsächliche Schwankungen des Sehwinkels
Der Mond umläuft die Erde in einer Ellipse, seine Entfernung schwankt dabei zwischen 363.300 und 405.500 km. Der Monddurchmesser von 3.476 km beträgt weniger als 1 % dieser Distanzen, weshalb das Bogenmaß des gesuchten Winkels einfach als Verhältnis von Durchmesser zu Entfernung angesetzt werden kann (Kleinwinkelnäherung). Der Sehwinkel beträgt demnach 0,491° bis 0,548°, was einer Schwankung von ± 5,5 % um den Mittelwert entspricht. Diese Spanne von 11 % ist zu klein, um ohne direkten Vergleich mit dem Auge zuverlässig erkannt zu werden. Der Ausdruck Supermond steht jedoch seit den 2010er Jahren für den besonders großen Vollmond in Erdnähe. Eine Veränderung des scheinbaren Durchmessers vom Apogäum zum Perigäum von ca. 13 %, verteilt über mehrere Jahre, ist für den menschlichen Beobachter nicht wahrnehmbar.
Betrachtet man den Mond unter geringem Höhenwinkel, also nahe dem Horizont, so sieht man seine Kontur in seiner Entfernung, die von Mitte bis Mitte der zwei Himmelskörper Erde und Mond gerechnet wird. Steht der Mond hingegen im Zenit, so ist man ihm als Betrachter um den Erdradius von gut 6.000 km, also fast 2 %, näher. Objektiv ist also der Mond, wenn er 40° oder höher am Himmel steht, unter einem mehr als 1 % größeren Sehwinkel sichtbar, als tief am Horizont – das ist geringfügig, doch gerade entgegen dem subjektiven Eindruck.
Durch die variierende Refraktion der Atmosphäre mit ihrer verlaufenden Dichte wird das Bild des Mondes tief am Horizont allerdings tendenziell (flach-)oval verzerrt. Der Sehwinkel der Höhe des Mond-Abbildes kann dann an dieser Sichtposition kleiner sein als bei höherem Stand des Mondes, die waagerechte Breite bleibt hingegen unverändert.
Literatur
- E. Bruce Goldstein: Wahrnehmungspsychologie. Eine Einführung. Spektrum Akademischer Verlag, Heidelberg u. a. 1997, ISBN 3-8274-0094-5, S. 243 ff.
- Joachim Herrmann: Warum erscheint uns der Mond am Horizont grösser als im Zenit? (= Veröffentlichung der Wilhelm-Förster-Sternwarte, Berlin. 16). Wilhelm-Foerster-Sternwarte, Berlin 1962. (Auch in: Kosmos 58, 1962, Heft 2, ISSN 0023-4230, S. 3 f.).
- Maurice Hershenson (Hrsg.): The Moon illusion. L. Erlbaum Associates, Hillsdale NJ 1989, ISBN 0-8058-0121-9.
- Lloyd Kaufman, James H. Kaufman: Explaining the moon illusion. In: Proceedings of the National Academy of Sciences. Band 97, Nummer 1, Januar 2000, S. 500–505. PMID 10618447, PMC 26692 (freier Volltext).
- Helen Ross, Cornelis Plug: The Mystery of The Moon Illusion. Exploring Size Perception. Oxford University Press, Oxford 2002, ISBN 0-19-850862-X.
Einzelnachweise
- Maurice Hershenson: The Moon Illusion. Project Syndicate, A World of Ideas (5. März 2004).
- Stephan Mayer: Das abgeflachte Firmament.
- P. Goüye: Diverse Observations de Physique Generale. In: Histoire de l’Acad. Royale des Sciences. Année 1700. Paris 1703, S. 8.
- K. Lühr: Die scheinbare Vergrößerung der Gestirne in der Nähe des Horizonts. In: Mitth. d. Ver. v. Freunden d. Astron. und kosm. Physik. 8, 1898, S. 31–35.
- V. Cornish: Apparent Enlargement of the Sun at the time of Rising and Setting. In: Nature. 140, 1937, S. 1082–1083.
- E. Schur: Mondtäuschung und Sehgrößenkonstanz. In: Psychologische Forschung. 7, 1926, S. 44–80.
- L. Kaufman, I. Rock: Scientific American. Jul 1962, S. 120–130.
Weblinks
- Ausführliche Erklärung zur „Mondtäuschung“ mit vielen Fotos, Zeichnungen und weiterführenden Links
- Was ist die Mondillusion? (Memento vom 19. Februar 2015 im Internet Archive) mit vielen Fotos
- Welf A. Kreiner: Warum ist heute der Mond so groß? Open Access Repositorium der Universität Ulm, 2001. doi:10.18725/OPARU-60
- W. A. Kreiner: Sonne, Mond und Ursa Major – ein informationstheoretisches Modell zur Größenwahrnehmung. Open Access Repositorium der Universität Ulm, doi:10.18725/OPARU-1213
- Englischsprachige Zusammenfassung verschiedener Theorien von D. E. Simanek
- Erklärung von Maurice Hershenson, Professor für Psychologie an der Brandeis University