Molekulare Mechanik

Die Molekulare Mechanik bedient sich der klassischen Mechanik, um molekulare Systeme zu modellieren. Die potentielle Energie aller Systeme wird in der molekularen Mechanik mittels Kraftfeldern berechnet. Die molekulare Mechanik kann verwendet werden um sowohl kleine Moleküle, größere biologische Systeme, beispielsweise Kanalproteine in Zellmembranen, bis hin zu makromolekularen Konstrukten mit tausenden Atomen zu untersuchen.

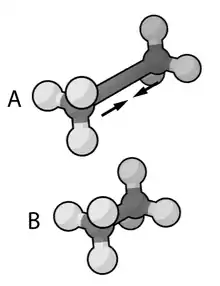
Ein Kraftfeld wird verwendet um die Bindungsenergie dieses Ethanmoleküls zu minimieren.

Vollständig atomistische Methoden haben die folgenden Eigenschaften:

jedes Atom wird als einzelnes Teilchen modelliert
jedem Teilchen wird ein Radius (typischerweise der Van-der-Waals-Radius), eine Polarisierbarkeit und eine konstante Nettoladung zugewiesen
Bindungsinteraktionen werden als „Federn“ behandelt, mit einer Gleichgewichtsauslenkung die der experimentellen, oder berechneten Bindungslänge entspricht

Variationen dieses Ansatzes sind möglich, beispielsweise haben einige Simulationen historisch eine united-atom-Darstellung verwendet, bei der jede Methylgruppe als einzelnes Teilchen behandelt wird. Große Proteinsysteme werden meist simuliert, indem ein Kugelmodell verwendet wird, bei dem jeder Aminosäure zwei oder vier Teilchen zugewiesen werden.

Funktionsform

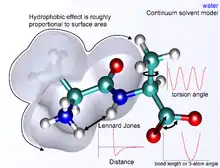
Potentielle Energiefunktion in der molekularen Mechanik.

Die folgende funktionelle Abstraktion, bekannt als potentielle Energiefunktion, oder Kraftfeld, berechnet die potentielle Energie $E$ eines molekularen Systems in einer gegebenen Konformation als Summe der individuellen Energieterme:

E=E_{\text{kovalent}}+E_{\text{nichtkovalent}}

wobei die Komponenten der kovalenten und nichtkovalenten Beiträge gegeben sind durch:

E_{\text{kovalent}}=E_{\text{Bindung}}+E_{\text{Winkel}}+E_{\text{Dieder}}

E_{\text{nichtkovalent}}=E_{\text{elektrostatisch}}+E_{\text{van der Waals}}

Die exakte Funktionsform der potentiellen Energiefunktion, und damit das entsprechende Kraftfeld, hängt von dem jeweilig verwendeten Simulationsprogramm ab. Allgemein werden die Bindungs- und Winkelterme als harmonische Potentiale modelliert. Die Energieminima dieser Potentiale liegen in etwa bei den Bindungslängen des Moleküls, die entweder experimentell bestimmt, oder durch Software mittels ab-initio-Verfahren ermittelt wird. Für eine akkurate Reproduktion der Schwingungsspektren kann das Morse-Potential verwendet werden, allerdings zulasten des Berechnungsaufwandes. Die Dieder- und Torsionsterme haben typischerweise mehrere Minima und können daher nicht als harmonische Oszillatoren modelliert werden. Diederterme können absichtlich „falsche“ Ausdrücke beinhalten, die als Korrektur für Abweichungen außerhalb der Ebene funktionieren (zum Beispiel um Benzol-Ringe planar zu halten, oder korrekte Geometrie und Chiralität von tetraedrischen Atomen zu gewährleisten).

Die nicht-Bindungs-Terme sind erheblich aufwendiger zu berechnen, da ein typisches Atom lediglich an wenige Partner direkt (z. B. kovalent) gebunden ist, tatsächlich aber mit jedem anderen Atom im Molekül wechselwirkt. Glücklicherweise nimmt der Einfluss des Van-der-Waals-Terms mit der Entfernung rapide ab – er wird üblicherweise durch ein „6–12 Lennard-Jones-Potential“ modelliert, was bedeutet, dass anziehende Kräfte mit der Entfernung mit r⁻⁶, und abstoßende Kräfte mit r⁻¹² abnehmen, wobei r die Entfernung zwischen zwei Atomen ist. Der abstoßende Teil r⁻¹² ist physikalisch allerdings nicht ganz korrekt, da die Abstoßungskraft eigentlich exponentiell abfällt. Die Beschreibung der Van-der-Waals-Kräfte durch „6–12 Lennard-Jones-Potentiale“ beinhaltet also Ungenauigkeiten, die bei kurzen Entfernungen durchaus signifikant werden können.[1] In der Regel wird ein cutoff-Radius verwendet um die Berechnungszeit zu verkürzen; dabei werden Wechselwirkungen von Atomen, deren Entfernung oberhalb des cutoff-Radius liegt, vernachlässigt.

Die elektrostatischen Terme sind schwierig zu berechnen, da diese nicht so schnell mit zunehmender Distanz abfallen. Elektrostatische Wechselwirkungen über lange Entfernungen sind aber häufig wichtige Einflüsse auf das zu untersuchende System (speziell für Proteine). Die grundlegende Funktionsform ist das Coulomb-Potential, welches lediglich mit r⁻¹ abfällt. Eine Reihe von Methoden kann verwendet werden, um dieses Problem zu umgehen; als einfachste Lösung bietet sich ein cutoff-Wert wie bei den Van-der-Waals-Termen an. Dadurch wird allerdings eine scharf abgegrenzte Unstetigkeit zwischen Atomen innerhalb und außerhalb des cutoff-Radius eingeführt, was nicht erwünscht ist. Durch Schalt- oder Skalierungsfunktionen, die die scheinbare elektrostatische Energie durch einen kontinuierlichen Faktor zwischen 0 und 1 im Bereich des cutoff-Radius „ausblenden“, lässt sich dieses Problem etwas präziser nähern. Andere, differenziertere, aber auch berechnungsintensivere Methoden sind bekannt als Particle-Mesh-Ewald-Methode (PME-Methode) und Multipol-Algorithmus.

Zusätzlich zur Funktionsform jedes Energieterms müssen einer sinnvollen Energiefunktion Parameter für Kraftkonstanten, Van-der-Waals-Faktoren und andere Konstanten zugewiesen werden. Diese Konstanten sind, zusammen mit der Gleichgewichtsbindungslänge, Bindungswinkel, Diederwinkel, Partialladungen, Atommassen und -radien und den Definitionen der Energiefunktionen, unter dem Begriff Kraftfeld zusammengefasst. Die Parametrisierung erfolgt typischerweise durch eine Abstimmung mit empirischen Daten und theoretisch berechneten Werten.

Jedes Kraftfeld ist so parametrisiert, dass es intern konsistent ist, die Parameter sind jedoch im Allgemeinen nicht von einem Feld auf ein anderes übertragbar.

Anwendungsgebiete

Die hauptsächliche Anwendung der molekularen Mechanik ist das Feld der Molekulardynamik-Simulation. Diese macht Gebrauch von Kraftfeldern, um die Kräfte zu berechnen die auf jedes einzelne Teilchen wirken und damit Bewegungsabläufe vorherzusagen. Vorausgesetzt es liegen genügend empirische Daten vor, lassen sich unter Annahme der Ergodenhypothese aus den molekulardynamischen Bewegungsabläufen thermodynamische, oder kinetische Parameter wie zum Beispiel die Reaktionsgeschwindigkeit abschätzen.

Eine andere Anwendung der molekularen Mechanik ist die Energieminimierung, wobei Kraftfelder als Optimierungskriterien verwendet werden. Diese Methode verwendet einen geeigneten Algorithmus (z. B. das Gradientenverfahren), um die molekulare Struktur eines lokalen Energieminimums zu finden. Diese Minima entsprechen stabilen Konformeren des Moleküls. Molekulare Bewegung kann als Vibrationen um – und gegenseitige Umwandlung zwischen diesen stabilen Konformeren modelliert werden.

Es ist daher üblich, Methoden zur lokalen Energieminimierung mit solchen zur globalen (im Rahmen der Simulation) Energieoptimierung zu kombinieren, um ein allgemeines Energieminimum zu finden. Bei begrenzten (endlichen) Temperaturen liegen Moleküle die meiste Zeit in Zuständen vor, die diesen Energieminima entsprechen, was diese wichtig für die Bestimmung der Moleküleigenschaften macht. Globale Optimierung kann durch Simulated Annealing, den Metropolisalgorithmus und andere Monte-Carlo-Simulationen erreicht werden. Alternativ können verschiedene deterministische Methoden diskreter oder kontinuierlicher Optimierung verwendet werden. Während ein Kraftfeld nur die enthalpische Komponente der freien Gibbs-Energie repräsentiert, ist es möglich die entropische Komponente durch die Verwendung von zusätzlichen Methoden, wie der Analyse von Schwingungsmoden mit einzubeziehen.

Potentielle Energiefunktionen in der molekularen Mechanik wurden bereits verwendet um Bindungskonstanten,[2][3][4][5][6] die Kinetik von Proteinfaltung,[7] Protonierungsgleichgewichte,[8] Koordinaten molekularen Dockings,[4][9] und Proteinbindungsstellen zu ermitteln.[10]

Umgebung und Solvatation

Es gibt mehrere Möglichkeiten, die Umgebung eines Moleküls zu definieren. Es kann zum einen im Vakuum als sogenannte Gasphasen-Simulation modelliert werden, wobei die Umgebung vollständig vernachlässigt wird. Dies ist jedoch nicht erstrebenswert, da speziell bei geladenen Verbindungen Fehler in der molekularen Geometrie auftreten können. Oberflächenladungen, die normalerweise mit Molekülen des Lösemittels wechselwirken würden, interagieren stattdessen miteinander, wobei Konformationen entstehen die in tatsächlichen Umgebungen sehr unwahrscheinlich, oder unmöglich sind. Die „beste“ Art, Solvatisierung zu modellieren ist es, ausdrücklich Lösemittelmoleküle in der Simulation zu platzieren und nicht anders zu behandeln als das interessierende Molekül selbst.

Erwartungsgemäß steigt der Berechnungsaufwand mit der Komplexität einer solchen Simulation. Die Komplexität von Modellen des Wassers als Lösemittel zum Beispiel reicht von der Darstellung als einfache, harte Kugel, bis zu vier oder fünf separaten Interaktionspunkten, die selbst die freien Elektronenpaare des Sauerstoffatoms berücksichtigen.

Ein Kompromiss aus Genauigkeit und Rechenaufwand kann durch implizite Solvatisierung erreicht werden, wobei die explizit dargestellten Lösemittelmoleküle durch mathematische Ausdrücke ersetzt werden, die das Verhalten des Lösemittels nähern. Diese Methode ist nützlich um die Fehler einer Vakuumsimulation zu vermeiden, vermag es aber nicht, interessierende Wechselwirkungen zwischen Lösemittel und Molekül genau darzustellen.

Beispiele für Softwarepakete

ACEMD - GPU MD
Abalone
AMBER
Ascalaph
BOSS
CHARMM
COSMOS
CytoSolve
Ghemical
GROMOS
GROMACS
ICM
MacroModel
MDynaMix
NAMD
Q
Q-Chem
Spartan
StruMM3D (STR3DI32)
TINKER
Zodiac
X-PLOR
Yasara
LAMMPS

Literatur

N. L. Allinger, U. Burkert: Molecular Mechanics. An American Chemical Society Publication, 1982, ISBN 0-8412-0885-9.
V. G. Box: The Molecular Mechanics of Quantized Valence Bonds. In: J Mol Model.. 3, Nr. 3, März 1997, S. 124–41. doi:10.1007/s008940050026.
V. G. Box: The anomeric effect of monosaccharides and their derivatives. Insights from the new QVBMM molecular mechanics force field. In: Heterocycles. 48, Nr. 11, 12. November 1998, S. 2389–417. doi:10.3987/REV-98-504.
V. G. Box: Stereo-electronic effects in polynucleotides and their double helices. In: J Mol Struct.. 689, Nr. 1–2, 2004, S. 33–41. bibcode:2004JMoSt.689...33B. doi:10.1016/j.molstruc.2003.10.019.
O. M. Becker: Computational biochemistry and biophysics. Marcel Dekker, New York, N.Y. 2001, ISBN 0-8247-0455-X.
A. D. Mackerell: Empirical force fields for biological macromolecules: overview and issues. In: J Comput Chem. 25, Nr. 13, Oktober 2004, S. 1584–604. doi:10.1002/jcc.20082. PMID 15264253.
T. Schlick: Molecular modeling and simulation: an interdisciplinary guide. Springer, Berlin 2002, ISBN 0-387-95404-X.
Krishnan Namboori, K. S. Ramachandran, Deepa Gopakumar: Computational Chemistry and Molecular Modeling: Principles and Applications. Springer, Berlin 2008, ISBN 3-540-77302-9.

Weblinks

Commons: Molekulare Mechanik – Sammlung von Bildern, Videos und Audiodateien

Chemgapedia − Molecular Modeling: Kraftfelder und Molekülmechanik
Hendrik Bekker: Molecular dynamics simulation methods revised (Dissertation, Englisch)
Molecular mechanics - it is simple

Einzelnachweise

Zgarbova M, et al.: Large-scale compensation of errors in pairwise-additive empirical force fields: comparison of AMBER intermolecular terms with rigorous DFT-SAPT calculations. In: Phys. Chem. Chem. Phys.. 12, 2010, S. 10476–10493. bibcode:2010PCCP...1210476Z. doi:10.1039/C002656E.
Kuhn B, Kollman PA: Binding of a diverse set of ligands to avidin and streptavidin: an accurate quantitative prediction of their relative affinities by a combination of molecular mechanics and continuum solvent models. In: Journal of Medicinal Chemistry. 43, Nr. 20, Oktober 2000, S. 3786–91. doi:10.1021/jm000241h. PMID 11020294.
Huo S, Massova I, Kollman PA: Computational alanine scanning of the 1:1 human growth hormone-receptor complex. In: J Comput Chem. 23, Nr. 1, Januar 2002, S. 15–27. doi:10.1002/jcc.1153. PMID 11913381.
Mobley DL, Graves AP, Chodera JD, McReynolds AC, Shoichet BK, Dill KA: Predicting absolute ligand binding free energies to a simple model site. In: J Mol Biol.. 371, Nr. 4, August 2007, S. 1118–34. doi:10.1016/j.jmb.2007.06.002. PMID 17599350. PMC 2104542 (freier Volltext).
Wang J, Kang X, Kuntz ID, Kollman PA: Hierarchical database screenings for HIV-1 reverse transcriptase using a pharmacophore model, rigid docking, solvation docking, and MM-PB/SA. In: Journal of Medicinal Chemistry. 48, Nr. 7, April 2005, S. 2432–44. doi:10.1021/jm049606e. PMID 15801834.
Kollman PA, Massova I, Reyes C, et al.: Calculating structures and free energies of complex molecules: combining molecular mechanics and continuum models. In: Acc Chem Res.. 33, Nr. 12, Dezember 2000, S. 889–97. doi:10.1021/ar000033j. PMID 11123888.
Snow CD, Nguyen H, Pande VS, Gruebele M: Absolute comparison of simulated and experimental protein-folding dynamics. In: Nature. 420, Nr. 6911, November 2002, S. 102–6. bibcode:2002Natur.420..102S. doi:10.1038/nature01160. PMID 12422224.
Barth P, Alber T, Harbury PB: Accurate, conformation-dependent predictions of solvent effects on protein ionization constants. In: Proc Natl Acad Sci U.S.A.. 104, Nr. 12, März 2007, S. 4898–903. bibcode:2007PNAS..104.4898B. doi:10.1073/pnas.0700188104. PMID 17360348. PMC 1829236 (freier Volltext).
Chakrabarti R, Klibanov AM, Friesner RA: Computational prediction of native protein ligand-binding and enzyme active site sequences. In: Proc Natl Acad Sci U.S.A.. 102, Nr. 29, Juli 2005, S. 10153–8. bibcode:2005PNAS..10210153C. doi:10.1073/pnas.0504023102. PMID 15998733. PMC 1177389 (freier Volltext).
Boas FE, Harbury PB: Design of Protein-Ligand Binding Based on the Molecular-Mechanics Energy Model. In: J Mol Biol.. 380, Nr. 2, Juli 2008, S. 415–24. doi:10.1016/j.jmb.2008.04.001. PMID 18514737. PMC 2569001 (freier Volltext).

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Zgarbova M, et al.: Large-scale compensation of errors in pairwise-additive empirical force fields: comparison of AMBER intermolecular terms with rigorous DFT-SAPT calculations. In: Phys. Chem. Chem. Phys.. 12, 2010, S. 10476–10493. bibcode:2010PCCP...1210476Z. doi:10.1039/C002656E.

[Kuhn-2] Kuhn B, Kollman PA: Binding of a diverse set of ligands to avidin and streptavidin: an accurate quantitative prediction of their relative affinities by a combination of molecular mechanics and continuum solvent models. In: Journal of Medicinal Chemistry. 43, Nr. 20, Oktober 2000, S. 3786–91. doi:10.1021/jm000241h. PMID 11020294.

[huo-3] Huo S, Massova I, Kollman PA: Computational alanine scanning of the 1:1 human growth hormone-receptor complex. In: J Comput Chem. 23, Nr. 1, Januar 2002, S. 15–27. doi:10.1002/jcc.1153. PMID 11913381.

[Mobley-4] Mobley DL, Graves AP, Chodera JD, McReynolds AC, Shoichet BK, Dill KA: Predicting absolute ligand binding free energies to a simple model site. In: J Mol Biol.. 371, Nr. 4, August 2007, S. 1118–34. doi:10.1016/j.jmb.2007.06.002. PMID 17599350. PMC 2104542 (freier Volltext).

[Wang-5] Wang J, Kang X, Kuntz ID, Kollman PA: Hierarchical database screenings for HIV-1 reverse transcriptase using a pharmacophore model, rigid docking, solvation docking, and MM-PB/SA. In: Journal of Medicinal Chemistry. 48, Nr. 7, April 2005, S. 2432–44. doi:10.1021/jm049606e. PMID 15801834.

[Kollman-6] Kollman PA, Massova I, Reyes C, et al.: Calculating structures and free energies of complex molecules: combining molecular mechanics and continuum models. In: Acc Chem Res.. 33, Nr. 12, Dezember 2000, S. 889–97. doi:10.1021/ar000033j. PMID 11123888.

[Snow-7] Snow CD, Nguyen H, Pande VS, Gruebele M: Absolute comparison of simulated and experimental protein-folding dynamics. In: Nature. 420, Nr. 6911, November 2002, S. 102–6. bibcode:2002Natur.420..102S. doi:10.1038/nature01160. PMID 12422224.

[Barth-8] Barth P, Alber T, Harbury PB: Accurate, conformation-dependent predictions of solvent effects on protein ionization constants. In: Proc Natl Acad Sci U.S.A.. 104, Nr. 12, März 2007, S. 4898–903. bibcode:2007PNAS..104.4898B. doi:10.1073/pnas.0700188104. PMID 17360348. PMC 1829236 (freier Volltext).

[Chakrabarti-9] Chakrabarti R, Klibanov AM, Friesner RA: Computational prediction of native protein ligand-binding and enzyme active site sequences. In: Proc Natl Acad Sci U.S.A.. 102, Nr. 29, Juli 2005, S. 10153–8. bibcode:2005PNAS..10210153C. doi:10.1073/pnas.0504023102. PMID 15998733. PMC 1177389 (freier Volltext).

[Boas-10] Boas FE, Harbury PB: Design of Protein-Ligand Binding Based on the Molecular-Mechanics Energy Model. In: J Mol Biol.. 380, Nr. 2, Juli 2008, S. 415–24. doi:10.1016/j.jmb.2008.04.001. PMID 18514737. PMC 2569001 (freier Volltext).