Marcus-Theorie

Die Marcus-Theorie[1] (benannt nach Rudolph Arthur Marcus) tritt bei Redoxreaktionen ohne Bindungsbildung oder Bindungsbruch an die Stelle der Eyring-Theorie. Beide Theorien führen zu Geschwindigkeitsgleichungen der gleichen exponentiellen Form. Während aber bei der Eyring-Theorie die Bindungsveränderungen der Reaktanten während der Reaktion bestimmend sind, spielt bei diesen Redoxreaktionen (Einelektronenaustauschreaktionen) das Lösungsmittel (outer sphere) die zentrale Rolle. Die Marcus-Theorie zeigt diese auf und erlaubt die Berechnung der Gibbsschen Freien Aktivierungsenthalpie aus den Polarisationseigenschaften des Lösungsmittels, der Größe und dem Abstand der Reaktanten bei der Elektronenübertragung und der freien Enthalpie der Redoxreaktion.

Hinführung

Chemische Reaktionen führen zu stofflichen Veränderungen. Sie können z. B. zur Substitution einer Gruppe im Molekül oder eines Liganden im Komplex führen, der Abspaltung eines Molekülteils oder eines Liganden oder zu einer Umlagerung. Es kann sich aber auch nur der Ladungszustand der Reaktionsteilnehmer ändern, und diese Redoxreaktionen scheinen in der anorganischen Chemie bei Ionen und Komplexen besonders einfach zu sein. Zu beobachten sind solche Reaktionen bei Ionen der Übergangsmetalle oft an Farbänderungen, aber auch organische Moleküle können sich bei Elektronenaufnahme bzw. -abgabe verfärben wie das Herbizid Paraquat (1,1'-Dimethyl-4,4’-bipyridinium), das bei Elektronenaufnahme blau wird. Daher stammt auch der alternative Name Methylviologen. Für einen Typ der Redoxreaktionen ohne Strukturveränderungen hat Marcus seine Theorie entwickelt. Für die mathematische Argumentation sollten die Originalarbeiten herangezogen werden.[2][3]

In einer Redoxreaktion fungiert ein Partner als Elektronendonor D, der andere als Elektronenakzeptor A. Damit die Partner reagieren können, müssen sie zusammen diffundieren. Sie bilden dabei den sogenannten Precusorkomplex, meist ein kinetischer instabiler solvatisierter Stoßkomplex, der durch die Elektronenübertragung in einen Successorkomplex übergeht, der seinerseits auseinander diffundiert. Für die Einelektronenübertragung ergibt dies die Reaktionsgleichung

\mathrm {D+A\ {\overset {\xrightarrow {k_{12}}}{\xleftarrow[{k_{21}}]{}}}\ [D{\dotsm }A]\ {\overset {\xrightarrow {k_{23}}}{\xleftarrow[{k_{32}}]{}}}\ [D^{+}{\dotsm }A^{-}]{\xrightarrow {k_{30}}}\ D^{+}+A^{-}}

(D und A können selbst Ladungen tragen). Dabei sind k₁₂, k₂₁ und k₃₀ Diffusionskonstanten, k₂₃ und k₃₂ Geschwindigkeitskonstanten aktivierter Teilreaktionen. Die Gesamtreaktion kann diffusionskontrolliert sein, wenn die Elektronenübertragung schneller ist als die Diffusion. Jeder Stoß führt dabei zu einer Reaktion. Ist die Reaktion aktivierungskontrolliert stellt sich das Assoziationsgleichgewicht ein, wobei die Elektronenübertragung der langsamere Schritt und die Trennung des Successorkomplexes der schnellere Schritt ist.

Redoxreaktionen finden meist in polaren Lösungsmitteln statt, Donor- und Akzeptorzentren tragen dann eine Solvathülle, und auch Precursor- und Sucessorkomplex sind solvatisiert. Die inneren Moleküle der Solvathülle, die sehr fest gebunden sind, bei Komplexen auch die Liganden, werden als innere Sphäre bezeichnet. Redoxreaktionen, an denen diese Sphäre beteiligt ist, nennt man „inner-sphere“-Reaktionen. Die äußere Sphäre besteht aus den freien Lösungsmittelmolekülen. Bei den „outer-sphere“-Reaktionen verändert sich die innere Sphäre nicht, es werden keine Bindungen gebrochen oder gebildet.

R. A. Marcus hat sich mit dem Wesen und der Größe der Freien Aktivierungsenthalpie bei Redoxreaktionen, genauer Ein-Elektronentransfer-Reaktionen des outer-sphere-Typs, beschäftigt und die zentrale Rolle des Lösungsmittels erkannt. Er hat zunächst zwei Arbeiten veröffentlicht.[2][3] Deren Ergebnisse werden häufig als Marcus-Theorie bezeichnet, obwohl Marcus’ Arbeiten später weit darüber hinausgehen.[1]

Das Problem

Bei outer-sphere Redoxreaktionen werden keine Bindungen geknüpft oder gebrochen. Es findet nur ein Elektronentransfer (ET) statt. Ein einfaches Beispiel ist die Fe²⁺/Fe³⁺ Redoxreaktion. Bei der Selbstaustauschreaktion, die in einer wässrigen Lösung, die z. B. sowohl FeSO₄ als auch Fe₂(SO₄)₃ enthält, in beiden Richtungen mit gleicher messbarer Bruttogeschwindigkeit stattfindet, ist die thermodynamische freie Standard-Reaktionsenthalpie (ΔG⁰) gleich Null.

Aus der Temperaturabhängigkeit der Geschwindigkeit z. B. einer Reaktion wie der S_N2-Substitutionsreaktion der Verseifung eines Alkylhalogenids, wird meist eine Aktivierungsenergie bestimmt, und diese wiederum als Energie eines Übergangszustandes im Reaktionsdiagramm charakterisiert. Letzteres wird nach Arrhenius und Eyring als Energiediagramm mit der Reaktionskoordinate als Abszisse gezeichnet, die den energetisch günstigsten Weg von den Edukten zu den Produkten beschreibt. Dabei sind die Punkte der Reaktionskoordinaten eine Folge von Kombinationen von Abständen und Winkeln zwischen und in den Reaktanten im Laufe der Bildung und/oder des Bruchs von Bindungen. Das Maximum im Energiediagramm – der Übergangszustand – ist durch eine ganz bestimmte Konfiguration der Atomkerne gekennzeichnet. In der Theorie des Übergangszustandes von Eyring[4][5] ist auch eine ganz bestimmte Kernkoordinatenänderung für das Überqueren des Maximums verantwortlich, weshalb die Schwingung in dieser Koordinatenrichtung in der Eyring-Theorie als Translation behandelt wird.

Bei den outer-sphere Redoxreaktionen kann es diesen Reaktionsweg nicht geben. Dennoch beobachtet man eine Aktivierungsenergie. Dabei hat die Geschwindigkeitskonstante für die aktivierungskontrollierte Reaktion dieselbe Form wie die Eyringsche Gleichung

k_{act}=A\cdot e^{-{\frac {\Delta G^{\ddagger }}{RT}}}

In $A$ wirkt vor allem die Übergangswahrscheinlichkeit und $\Delta G^{\ddagger }$ ist die freie Enthalpie für die Bildung des Übergangszustandes.

Das Modell von Marcus

Beim Elektronenaustausch verändert sich die Ladungsverteilung und dies hat große Auswirkungen auf die Lösungsmittelumgebung, denn die Lösungsmittelmoleküle richten sich im Feld der Ladungen aus (man nennt dies Orientierungspolarisation), und auch die Atome und Elektronen in den Lösungsmittelmolekülen werden leicht verschoben (Atom- bzw. Elektronenpolarisation). Diese Lösungsmittelpolarisation beeinflusst bei Redoxreaktionen maßgeblich die Größe der Aktivierungsenergie und damit die Reaktionsgeschwindigkeit.

Substitutions-, Eliminierungs- und Isomerisierungsreaktionen unterscheiden sich von den outer-sphere Redoxreaktionen aber nicht nur durch Strukturänderungen, sondern auch dadurch, dass alle einzelnen Kern- und Ladungsverschiebungen (Ladungstransfer, charge transfer, CT) in den Reaktanten auf dem energiegünstigsten Reaktionsweg konzertiert ablaufen, die Kernkonfigurationen sind damit relativ zueinander stets im „Gleichgewicht“ – das Energiemaximum tritt also nur in einer Dimension der Potentialhyperfläche auf, in allen anderen liegt weiterhin ein Minimum vor. Ein Beispiel ist die S_N2-Substitution der Hydrolyse eines Alkylhalogenids, bei dem durch den Rückseitenangriff des OH⁻-Ions ein Halogenidion verdrängt und die über einen Übergangszustand mit einem fünfbindigen Kohlenstoffatom verläuft. Die Reaktantensysteme sind im Lauf der Reaktion so stark gekoppelt, dass sie ein einheitliches Gebilde und schließlich einen aktivierten Komplex darstellen. Das Lösungsmittel hat einen zwar nicht zu vernachlässigenden, im Vergleich dazu jedoch nur kleinen Einfluss.

Bei outer-sphere Redoxreaktionen sind die Kernverschiebungen in den Reaktanten sehr klein, dagegen ist das Lösungsmittel bestimmend. Die Kopplung von Donor und Akzeptor ist schwach, beide behalten während der ganzen Reaktion ihre Identität. Deshalb kann das Elektron als Elementarteilchen nur als Ganzes „springen“ (Elektronentransfer ET). Der Elektronensprung, wenn er denn stattfindet, ist sehr viel schneller als sich die Lösungsmittelmoleküle bewegen können (Born-Oppenheimer-Näherung). Die Konsequenz ist: damit das Elektron springen kann, müssen die Kernpositionen der beiden Reaktanten und aller Lösungsmittelmoleküle vor und nach dem schnellen Elektronensprung die gleiche sein (Franck-Condon-Prinzip);[6] und auch die Energie darf sich beim Elektronensprung nicht ändern.

Die Lösungsmittelanordnung ist von den Ladungsverhältnissen abhängig. Wenn sie vor und nach dem Elektronensprung die gleiche sein soll, dann wäre jede richtige Anordnung für die Selbstaustauschreaktion schon aus Symmetriegründen durch eine Lösungsmittelkonfiguration verwirklicht, die sich bei der Übertragung einer halben Elementarladung einstellte. Gleichzeitig hätten in dieser Lösungsmittelumgebung Precursor- und Sucessorkomplex die gleiche Energie. In dieser Lösungsmittelanordnung wären die Bedingungen für den Elektronensprung erfüllt.

Weil das Elektron als Elementarteilchen aber nicht geteilt werden kann, muss es entweder auf dem Ausgangs- oder Zielatom oder -molekül lokalisiert sein. Damit sind im „Übergangszustand“ Lösungsmittelkonfiguration (entspräche der Übertragung einer halben Ladung) und Ladungsverteilung (Ladung auf einem der Partner) nicht im „Gleichgewicht“. Dennoch muss dieser Übergangszustand vor dem Elektronensprung erreicht werden, und dies kann durch thermische Fluktuationen im Lösungsmittel geschehen. Die Erzeugung der richtigen Lösungsmittelkonfiguration und der Elektronensprung sind gewissermaßen entkoppelt und geschehen nicht mehr synchron. Eigentlich haben sie nichts miteinander zu tun. Die Energie des Übergangszustandes ist also zum größten Teil eine Polarisationsenergie des Lösungsmittels.

Die Marcus-Theorie

Das makroskopische System: zwei leitende Kugeln

Abb. 1. Die Parabeln der outer-sphere Reorganisationsenergie des Systems zwei Kugeln im Lösungsmittel. Parabel i: Ladung auf der ersten,Ladungsübertragung auf die zweite, Parabel f: Ladung auf der zweiten, Übertragung zur ersten. Die Abszisse ist die übertragene Ladungsmenge Δe bzw. die dadurch verursachte Polarisation P, die Ordinate die Freie Enthalpie. ΔG(0)^‡ = λ_o/4 ist die Reorganisationsenergie bei Δe = 0,5, sie entspräche der Aktivierungsenthalpie der Selbstaustauschreaktion.

Auf Grund dieser Überlegungen hat Rudolph A. Marcus eine klassische Theorie entwickelt. Ihr Ziel ist die Berechnung der Polarisationsenergie des erwähnten Nichtgleichgewichtszustandes. Aus der Thermodynamik weiß man, dass die Energie eines solchen berechnet werden kann, wenn man einen reversiblen Weg dahin findet. Dies ist Marcus gelungen.

Vier Elemente sind konstitutiv für das der Theorie zugrunde liegende Modell: (1) Marcus benutzt zunächst ein klassisches, rein elektrostatisches Modell, bei dem die Ladung (sehr viele Elementarladungen) in beliebigen Portionen zwischen zwei Körpern übertragen werden kann. (2) Marcus trennt die schnelle Elektronenpolarisation P_e des Lösungsmittels und die langsame Atom- und Orientierungspolarisation P_u auf Grund der um Zehnerpotenzen verschiedenen Zeitkonstanten, mit denen sie sich einstellen. (3) Marcus trennt innere Sphäre (Reaktant + fest solvatisierte Lösungsmittelhülle, bei Komplexen: + Liganden) und die äußere Sphäre (freies Lösungsmittel außerhalb). (4) Marcus berechnet hier nur die outer-sphere Energie der Nichtgleichgewichtspolarisation des „Übergangszustands“ in einem Lösungsmittel, die wegen der weit reichenden elektrostatischen Kräfte (vgl. die Debye-Hückel-Theorie der Elektrochemie) meist wesentlich größer ist als der Beitrag der inneren Sphäre. Dazu wählt er einen Weg über zwei reversible Auf- bzw. Umladungsschritte.

Das Werkzeug liefert die Theorie der dielektrische Polarisation in Lösungen. Marcus löst das Problem allgemein für eine Ladungsübertragung zwischen 2 Körpern beliebiger Gestalt mit bestimmten Volum- und Oberflächenladungen. Für den Fall der Selbstaustausch-Redoxreaktion wird das Redoxpaar (z. B. Fe(H₂O)₆³⁺/Fe(H₂O)₆²⁺) durch zwei makroskopische, leitende Kugeln bestimmten Ladungszustandes in bestimmtem Abstand ersetzt, zwischen denen eine bestimmte Ladungsmenge reversibel ausgetauscht werden soll.

Im ersten Schritt wird die Energie W_I des Zustands berechnet, in dem beide Kugeln je die Hälfte der auszutauschenden Ladung tragen. Dieser Zustand kann durch die reversible Übertragung der halben Ladungsmenge von der einen zur andern Kugel durch die Überführung dieser Austauschladung von der Donor-Kugel ins Vakuum und von dort auf die Akzeptor-Kugel erreicht werden.[7] Die so geladenen Kugeln erzeugen im Lösungsmittel ein bestimmtes elektrisches Feld, in dem sich die Gesamt-Lösungsmittelpolarisation P_e + P_u einstellt. Andererseits erzeugt nun auch die Polarisation des Lösungsmittels einen Feldanteil, der auf Ladung und Polarisation zurückwirkt.

Im zweiten Schritt wird die Energie W_II der reversiblen (Rück-)Übertragung der halben ausgetauschten Ladung, wieder über das Vakuum, auf die erste Kugel bestimmt. Dabei wird aber die Atom- und Orientierungspolarisation P_u festgehalten, lediglich die Elektronenpolarisation kann sich im Feld der neuen Ladungsverteilung und der nun festen P_u einstellen. Danach befindet sich das System in dem angestrebten Zustand mit einer Elektronenpolarisation, die dem Ausgangszustand der Redoxreaktion entspricht, und einer Atom- und Orientierungspolarisation, die dem aktivierten Komplex entsprechen. Die Energie W_I + W_II dieses Zustands ist thermodynamisch eine freie Enthalpie G.

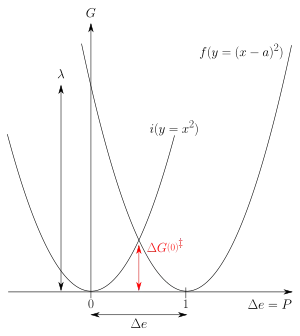
Natürlich ist in diesem klassischen Modell die Ladungsübertragung nicht nur für die halbe Ladungsmenge, sondern auch für andere Portionen Δe möglich. So kann man die Energie als Funktion der Verteilung der Ladung auf die beiden Kugeln und damit der Lösungsmittelpolarisation abtasten. Marcus hat auf diese elegante Weise die Koordinaten aller Lösungsmittelmoleküle in eine einzige Polarisationskoordinate Δp, die durch die Ladungsübertragung Δe bestimmt ist, zusammengefasst und damit eine Vereinfachung der Energiedarstellung in nur zwei Dimensionen erzielt: G = f(Δe). Das Ergebnis für zwei leitende Kugeln in einem Lösungsmittel ist die Marcus-Formel

G=\left({\frac {1}{2r_{1}}}+{\frac {1}{2r_{2}}}-{\frac {1}{R}}\right)\cdot \left({\frac {1}{\epsilon _{op}}}-{\frac {1}{\epsilon _{s}}}\right)\cdot (\Delta e)^{2}

wobei r₁ und r₂ die Radien der beiden Kugeln sind, R deren Abstand ist und ε_s und ε_op die statische und Hochfrequenz-(optische) Dielektrizitätskonstante des Lösungsmittels sind. Δe ist die übertragene Ladungsmenge, der Graph G vs. Δe ist eine Parabel (Abb. 1). In der Marcus-Theorie wird die Energie, die der Übertragung einer ganzen Ladung entspricht (Δe = 1) als (outer sphere) Reorganisationsenergie λ_o bezeichnet, d. h. die Energie des Zweikugelsystems, in dem die Polarisation der einer ganzen übertragenen Ladung entspricht, die Ladungsverteilung aber dem Zustand vor der Übertragung.[8] Das System ist symmetrisch in Bezug auf die Austauschrichtung.

Das mikroskopische System: das Redox-Paar

Abb. 2 Marcus-Parabeln für verschiedene Redoxreaktionen: f₁ für solche mit positivem ΔG⁰, f(0) für die Selbstaustauschreaktion mit ΔG⁰ = 0 (gestrichelt), f₂ für mäßig negatives ΔG⁰ (so gewählt, dass ΔG^‡ = 0) und f₃ für stark negatives ΔG⁰. Die freie Aktivierungsenergie ΔG^‡ (b₁) nimmt von f₁ (b) über f(0) (a) bis f₂ (Null) ab und steigt bei f₃ wieder an („Marcus invertiertes Gebiet“).

Bei Verkleinerung des klassischen Zwei-Kugel-Systems bis zur Selbstaustauschreaktion kommt man zum quantenbestimmten Redox-Paar, in dem die Ladung nicht mehr in beliebigen Portionen, sondern nur noch als eine ganze Elementarladung übertragen werden kann. Die Lösungsmittelpolarisation kann aber nach wie vor klassisch behandelt werden, d. h. sie ist nicht gequantelt, da sie durch sehr viele Lösungsmittelmoleküle gemeinsam bestimmt wird. Deshalb kann man die Reorganisationsenergie für eine hypothetische Übertragung und Rückübertragung einer Partial-Elementarladung nach der Marcus-Formel berechnen. Die Reorganisationsenergie ist auch für chemische Redoxsysteme eine Parabel (Abb. 2.), und sie entspricht einer freien Energie bzw. freien Enthalpie. Die Energie, die das System bei der hypothetischen Übertragung einer halben Elektronenladung (Δe = 0,5) hätte, ist die Aktivierungsenthalpie der Selbstaustauschreaktion ΔG(0)^‡ = λ_o/4 (vgl. Abb. 1 und Abb. 2, Schnittpunkt der Parabeln i und f bzw. f(0)).

Bis hierher war alles reine Physik, nun kommt etwas Chemie dazu. Die Selbstaustauschreaktion ist unter den Redoxreaktionen eine Besonderheit. Die meisten Redoxreaktionen laufen zwischen verschiedenen Partnern ab, z. B.

\mathrm {[Fe^{II}(CN)_{6}]^{4-}} +\mathrm {[Ir^{IV}Cl_{6}]^{2-}} \rightleftharpoons \mathrm {[Fe^{III}CN_{6}]^{3-}} +\mathrm {[Ir^{III}Cl_{6}]^{3-}}

und zeigen damit auch eine positive (endergonisch) oder negative (exergonisch) freie Reaktionsenthalpie ΔG⁰.

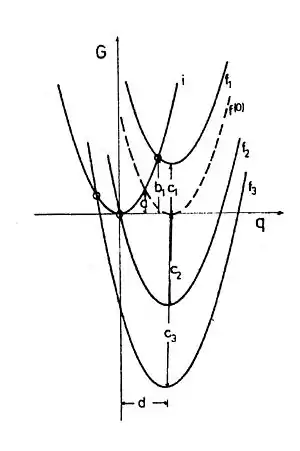
Da sich die Marcus-Berechnungen ausschließlich auf die elektrostatischen Verhältnisse im Lösungsmittel (outer-sphere) beziehen, sind ΔG⁰ und λ_o voneinander unabhängig und einfach additiv, d. h. die Marcus-Parabeln von Systemen mit verschiedenem ΔG⁰ sind im G vs. Δe − Diagramm lediglich nach oben oder nach unten verschoben (Abb. 2). Eine Variation von ΔG⁰ kann man experimentell beispielsweise dadurch erreichen, dass man einem Donor verschiedene Akzeptoren anbietet.

Aus einfacher Rechnung mit den Parabeln i (Gleichung y = x²), f(0) (Gleichung y = (x−d)²) und f₁ bis f₃ (Gleichung y = (x−d)² + c) ergibt sich für die freie Aktivierungsenthalpie

\Delta G^{\ddagger }={\frac {(\lambda _{o}+\Delta G^{0})^{2}}{4\lambda _{o}}}

Man sollte vielleicht nochmals betonen, dass der Schnittpunkt der Parabeln die Polarisationsenergie darstellt, nicht die Energie einer bestimmten Konfiguration aller Kerne der Reaktanten wie z. B. bei der erwähnten Substitutionsreaktion. Während idealiter bei dieser die Geometrie des Übergangszustands in jedem Reaktantenpaar dieselbe ist, können Redoxpaare mit vielen verschiedenen Polarisationsumgebungen die energetische Bedingung erfüllen. Schon deshalb ist die Verwendung der Freien Aktivierungsenergie als thermodynamische Größe angemessen.

Die Formel von Marcus (2) zeigt eine quadratische Beziehung zwischen freier Reaktionsenthalpie und freier Aktivierungsenthalpie. Es ist eine Erfahrung aus dem großen experimentellen Material der Chemie: Reaktionen verlaufen meist umso schneller, je negativer ΔG⁰ ist. In vielen Fällen wird sogar eine lineare freie Energie Beziehung (LFE) festgestellt. Auch nach der Marcus-Formel nehmen die Reaktionsgeschwindigkeiten zu, wenn die Reaktionen exergonischer werden, aber nur solange ΔG⁰ im positiven oder mäßig negativen Wertebereich liegt. Überraschend ist, dass die freie Aktivierungsenthalpie für Redoxreaktionen in Lösung nach der Formel (3) bei sehr stark negativer freier Reaktionsenthalpie wieder größer werden sollte, nämlich dann, wenn ΔG⁰ negativ und absolut größer ist als λ_o. Dieser Bereich der freien Reaktionsenthalpie wird „Marcus-invertiertes“ Gebiet genannt. In Abb. 2 sieht man, dass bei weiterem Absinken von ΔG⁰ der Schnittpunkt der i- und f-Parabeln nach links oben wandert, was eine Zunahme der freien Aktivierungsenthalpie und Abnahme der Geschwindigkeit bedeutet. Die Darstellung ln k vs. ΔG⁰ sollte also eine Maximumskurve sein.

Das Maximum der Reaktionsgeschwindigkeit wird bei ΔG^‡ = 0 erwartet. Hier ist auch Δe = 0 bzw. q = 0 (Abb. 2). Dies bedeutet, dass das Elektron bei der Gleichgewichts-Lösungsmittelpolarisation der Edukte springen kann, die natürlich viel wahrscheinlicher realisiert ist, als eine thermisch angeregte: die Reaktion ist dann barrierelos. Im invertierten Bereich entspricht die Polarisation der denkschwierigen Vorstellung einer hypothetischen Ladungsverteilung auf den Reaktanten, bei der der Donor Ladung aufgenommen und der Akzeptor Ladung abgegeben hätte. In Wirklichkeit geschieht das natürlich nicht, denn nicht eine reale Ladungsübertragung erzeugt diese Polarisation, sondern thermische Fluktuationen im Lösungsmittel. Die Polarisation, die für den invertierten Bereich nötig ist, kann sich mit einer gewissen Wahrscheinlichkeit durch die thermische Fluktuation ebenso gut einstellen jede andere gleicher Energie.[9] Das Elektron wartet gewissermaßen auf die richtige Polarisation, bis es springt.

Die experimentellen Ergebnisse

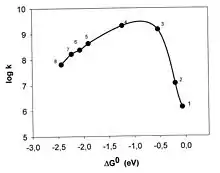
Abb. 3 Marcus-Verhalten in einem Molekül, das aus einem Biphenylteil, dessen Anion (erzeugt durch Pulsradiolyse) als Donor dient, einem Steroidteil, der als starrer Abstandshalter dient und verschiedenen aromatischen Kohlenwasserstoffen (1–3) und Chinonen (4–8), die als Akzeptoren dienen, besteht.[10]

Marcus hat seine Theorie 1956 publiziert. Über lange Jahre wurde das invertierte Gebiet gesucht, die Experimente ergaben jedoch bei Reaktionsreihen mit kleiner werdendem ΔG⁰ nur einen Anstieg von k bis zum diffusionskontrollierten Wert, d. h. zu dem Wert, bei dem jeder Zusammenstoß der Reaktanten zur Reaktion führt, und dieser Grenzwert blieb auch im Bereich sehr stark negativer ΔG⁰-Werte erhalten (Rehm-Weller-Verhalten).[11] Es hat ca. 30 Jahre gedauert, bis der invertierte Bereich von Miller, Calcaterra und Closs eindeutig nachgewiesen werden konnte und zwar bei der innermolekularen Elektronenübertragung in einem Molekül, in dem Donor und Akzeptor durch eine starre Brücke auf festem Abstand gehalten wurden (Abb. 3).[12]

Ex post kann man vermuten, dass bei frei diffundierenden Reaktionspartnern der Elektronensprung bei dem Abstand R erfolgt, bei dem λ_o = − ΔG⁰ ist, also ΔG^# = 0 ist. Denn λ_o ist von R abhängig, λ_o wird bei größerem R größer, die Öffnung der Parabel kleiner, und es ist formal immer möglich die Parabeln der Abb. 2 so zu verengen, dass die f-Parabel durch den Scheitel der i-Parabel geht. Das bedeutet, dass immer ΔG^‡ = 0 und die Geschwindigkeitskonstante k einen maximalen Wert, den der diffusionsbedingten Grenze, für alle Redoxreaktionen mit sehr negativer Reaktionsenthalpie ΔG⁰ annimmt.[13] Es gibt aber auch die Ansicht, dass eine Abnahme der Geschwindigkeit bei sehr schnellen Elektronenübertagungen jenseits der experimentell erreichbaren sehr negativen ΔG⁰-Werte liege. Auch die Beteiligung von angeregten Elektronenzuständen ist diskutiert worden[1].

R. A. Marcus und Mitarbeiter haben in den auf die Erstveröffentlichung der Theorie folgenden Jahren verschiedene Aspekte dieser Theorie verfeinert. Sie haben u. a. statistische Überlegungen und Quanteneffekte[14] berücksichtigt, sie auf Chemiluminszenzsysteme[15] und Elektrodenreaktionen[16] ausgeweitet. R. A. Marcus erhielt für seine Arbeiten 1992 den Nobelpreis für Chemie, sein Nobel-Vortrag[1] gibt eine umfassende Übersicht über sein Werk.

Belege und Anmerkungen

ELECTRON TRANSFER REACTIONS IN CHEMISTRY: THEORY AND EXPERIMENT. (PDF; 1,0 MB) In: Nobelstiftung. Abgerufen am 2. April 2007.oder Artikel in „Die Zeit“ dazu: hier
R. A. Marcus: On the Theory of Oxidation-Reduction Reactions Involving Electron Transfer. I. In: The Journal of Chemical Physics. Bd. 24, Nr. 5, 1956, S. 966–978, doi:10.1063/1.1742723.
R. A. Marcus: Electrostatic Free Energy and Other Properties of States Having Nonequilibrium Polarization I. In: The Journal of Chemical Physics. Bd. 24, Nr. 5, 1956, S. 979–989, doi:10.1063/1.1742724.
Peter W. Atkins: Physikalische Chemie. 2., korrigierter Nachdruck der 1. Auflage. Übersetzt und ergänzt von Arno Höpfner. VCH Verlagsgesellschaft, Weinheim u. a. 1990, ISBN 3-527-25913-9, S. 763–770.
R. Stephen Berry, Stuart A. Rice, John Ross: Physical Chemistry. Wiley, New York NY 1980, ISBN 0-471-04829-1, S. 1147 ff.
Willard F. Libby: Theory of Electron Exchange Reactions in Aqueous Solution. In: The Journal of Physical Chemistry. Bd. 56, Nr. 7, 1952, S. 863–868, doi:10.1021/j150499a010.
Marcus legt bei seinen Berechnungen den Energienullpunkt in den Vakuumzustand der Reaktanten. Deshalb enthalten viele seiner Gleichungen auch die Solvatatisierungsenergien der isolierten Reaktanten W_iso und die elektrostatische Bildungsenergie des Precusorkomplexes.
Die quadratische Abhängigkeit der outer-sphere Reorganisationsenergie ist keine Folge gequantelter Schwingungen in den Reaktanten oder im Lösungsmittel, die Theorie ist rein klassisch.
Die Rückreaktion kann vielleicht das Verständnis erleichtern: für diese genügt die Polarisation bei der hypothetischen Rückübertragung eines ganzen Elektrons nicht um eine Polarisation zu schaffen in der die Polarisationsenergien von A/D und A⁻ und D⁺ gleich groß sind. Diese Situation wird erst bei der hypothetischen Übertragung von mehr als einer Elementarladung erreicht.
Es wird empfohlen die Originalarbeit anzusehen, JACS gibt für Wikipedia keine Übernahmeerlaubnis für Abbildungen.
Dieter Rehm, Albert Weller: Kinetik und Mechanismus der Elektronenübertragung bei der Fluoreszenzlöschung in Acetonitril. In: Berichte der Bunsen-Gesellschaft für physikalische Chemie. Bd. 73, Nr. 8/9, 1969, S. 834–839, doi:10.1002/bbpc.19690730818, haben dieses Verhalten durch die empirische Formel $\Delta G^{\ddagger }={\frac {\Delta G^{0}}{2}}+{\sqrt {\Delta G^{\ddagger }(0)^{2}+\left({\frac {\Delta G^{0}}{2}}\right)^{2}}}$ beschrieben.
John R. Miller, L. T. Calcaterra, Gerhard L. Closs: Intramolecular long-distance electron transfer in radical anions. The effects of free energy and solvent on the reaction rates. In: Journal of the American Chemical Society. Bd. 106, Nr. 10, 1984, S. 3047–3049, doi:10.1021/ja00322a058.
Dafür sprechen die Ergebnisse von Arbeiten, in denen die Größe eines Komplexes systematisch verändert worden ist. (z. B.: Hermann Rau, Rolfdieter Frank, Gerhard Greiner: Rate Dependence of Electron Transfer on Donor-Acceptor Separation and on Free Enthalpy Change. The Ru(bpy)₃²⁺/Viologen²⁺ System. In: The Journal of Physical Chemistry. Bd. 90, Nr. 11, 1986, S. 2476–2481, doi:10.1021/j100402a042).
Paul Siders, R. A. Marcus: Quantum Effects in Electron-Transfer Reactions. In: Journal of the American Chemical Society. Bd. 103, Nr. 4, 1981, S. 741–747, doi:10.1021/ja00394a003; Paul Siders, R. A. Marcus: Quantum Effects for Electron-Transfer Reactions in the „Inverted Region“. In: Journal of the American Chemical Society. Bd. 103, Nr. 4, 1981, S. 748–752, doi:10.1021/ja00394a004.
R. A. Marcus: On the Theory of Chemiluminescent Electron-Transfer Reactions. In: The Journal of Chemical Physics. Bd. 43, Nr. 8, 1965, S. 2654–2657, doi:10.1063/1.1697190.
R. A. Marcus: On the Theory of Electron-Transfer Reactions. VI. Unified Treatment for Homogeneous and Electrode Reactions. In: The Journal of Chemical Physics. Bd. 43, Nr. 2, 1965, S. 679–701, doi:10.1063/1.1696792.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[Nobel-1] ELECTRON TRANSFER REACTIONS IN CHEMISTRY: THEORY AND EXPERIMENT. (PDF; 1,0 MB) In: Nobelstiftung. Abgerufen am 2. April 2007.oder Artikel in „Die Zeit“ dazu: hier

[Marcus_1-2] R. A. Marcus: On the Theory of Oxidation-Reduction Reactions Involving Electron Transfer. I. In: The Journal of Chemical Physics. Bd. 24, Nr. 5, 1956, S. 966–978, doi:10.1063/1.1742723.

[Marcus_2-3] R. A. Marcus: Electrostatic Free Energy and Other Properties of States Having Nonequilibrium Polarization I. In: The Journal of Chemical Physics. Bd. 24, Nr. 5, 1956, S. 979–989, doi:10.1063/1.1742724.

[4] Peter W. Atkins: Physikalische Chemie. 2., korrigierter Nachdruck der 1. Auflage. Übersetzt und ergänzt von Arno Höpfner. VCH Verlagsgesellschaft, Weinheim u. a. 1990, ISBN 3-527-25913-9, S. 763–770.

[5] R. Stephen Berry, Stuart A. Rice, John Ross: Physical Chemistry. Wiley, New York NY 1980, ISBN 0-471-04829-1, S. 1147 ff.

[6] Willard F. Libby: Theory of Electron Exchange Reactions in Aqueous Solution. In: The Journal of Physical Chemistry. Bd. 56, Nr. 7, 1952, S. 863–868, doi:10.1021/j150499a010.

[7] Marcus legt bei seinen Berechnungen den Energienullpunkt in den Vakuumzustand der Reaktanten. Deshalb enthalten viele seiner Gleichungen auch die Solvatatisierungsenergien der isolierten Reaktanten W_iso und die elektrostatische Bildungsenergie des Precusorkomplexes.

[8] Die quadratische Abhängigkeit der outer-sphere Reorganisationsenergie ist keine Folge gequantelter Schwingungen in den Reaktanten oder im Lösungsmittel, die Theorie ist rein klassisch.

[9] Die Rückreaktion kann vielleicht das Verständnis erleichtern: für diese genügt die Polarisation bei der hypothetischen Rückübertragung eines ganzen Elektrons nicht um eine Polarisation zu schaffen in der die Polarisationsenergien von A/D und A⁻ und D⁺ gleich groß sind. Diese Situation wird erst bei der hypothetischen Übertragung von mehr als einer Elementarladung erreicht.

[10] Es wird empfohlen die Originalarbeit anzusehen, JACS gibt für Wikipedia keine Übernahmeerlaubnis für Abbildungen.

[11] Dieter Rehm, Albert Weller: Kinetik und Mechanismus der Elektronenübertragung bei der Fluoreszenzlöschung in Acetonitril. In: Berichte der Bunsen-Gesellschaft für physikalische Chemie. Bd. 73, Nr. 8/9, 1969, S. 834–839, doi:10.1002/bbpc.19690730818, haben dieses Verhalten durch die empirische Formel $\Delta G^{\ddagger }={\frac {\Delta G^{0}}{2}}+{\sqrt {\Delta G^{\ddagger }(0)^{2}+\left({\frac {\Delta G^{0}}{2}}\right)^{2}}}$ beschrieben.

[12] John R. Miller, L. T. Calcaterra, Gerhard L. Closs: Intramolecular long-distance electron transfer in radical anions. The effects of free energy and solvent on the reaction rates. In: Journal of the American Chemical Society. Bd. 106, Nr. 10, 1984, S. 3047–3049, doi:10.1021/ja00322a058.

[13] Dafür sprechen die Ergebnisse von Arbeiten, in denen die Größe eines Komplexes systematisch verändert worden ist. (z. B.: Hermann Rau, Rolfdieter Frank, Gerhard Greiner: Rate Dependence of Electron Transfer on Donor-Acceptor Separation and on Free Enthalpy Change. The Ru(bpy)₃²⁺/Viologen²⁺ System. In: The Journal of Physical Chemistry. Bd. 90, Nr. 11, 1986, S. 2476–2481, doi:10.1021/j100402a042).

[14] Paul Siders, R. A. Marcus: Quantum Effects in Electron-Transfer Reactions. In: Journal of the American Chemical Society. Bd. 103, Nr. 4, 1981, S. 741–747, doi:10.1021/ja00394a003; Paul Siders, R. A. Marcus: Quantum Effects for Electron-Transfer Reactions in the „Inverted Region“. In: Journal of the American Chemical Society. Bd. 103, Nr. 4, 1981, S. 748–752, doi:10.1021/ja00394a004.

[15] R. A. Marcus: On the Theory of Chemiluminescent Electron-Transfer Reactions. In: The Journal of Chemical Physics. Bd. 43, Nr. 8, 1965, S. 2654–2657, doi:10.1063/1.1697190.

[16] R. A. Marcus: On the Theory of Electron-Transfer Reactions. VI. Unified Treatment for Homogeneous and Electrode Reactions. In: The Journal of Chemical Physics. Bd. 43, Nr. 2, 1965, S. 679–701, doi:10.1063/1.1696792.