Lichtfeld

Das Lichtfeld ist eine Funktion, welche die Lichtmenge beschreibt, die an jedem Punkt des dreidimensionalen Raums in alle Richtungen fällt.

Geschichte

Als erster beschrieb Michael Faraday in seinen Thoughts on Ray Vibration[1 1], dass Licht als Feld interpretiert werden kann, ähnlich dem magnetischen Feld, an dem Faraday für mehrere Jahre gearbeitet hatte. Der Begriff Lichtfeld wurde geprägt von Arun Gershun in einer Veröffentlichung über radiometrische Eigenschaften des Lichts im dreidimensionalen Raum[1 2]. In der jüngeren Geschichte der Computergrafik wurde dieser Begriff ein wenig umgedeutet.

Die plenoptische Funktion

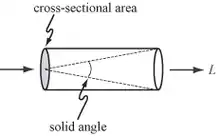
Die Strahldichte L entlang eines Strahls kann als die Lichtmenge aufgefasst werden, die sich entlang aller möglichen Geraden durch ein Rohr bewegt, dessen Größe durch seinen Raumwinkel und seine Querschnittsfläche bestimmt ist.

In der geometrischen Optik wird Licht durch Lichtstrahlen beschrieben (Das Konzept der geometrischen Optik beruht unter anderem auf der Annahme von inkohärenter Strahlung und Objektgrößen deutlich über der Lichtwellenlänge). Das Maß für die Menge an Licht, die entlang dieser Lichtstrahlen transportiert wird, ist die Strahldichte. Die Strahldichte wird mit L bezeichnet und wird gemessen in Watt (W) pro Steradiant (sr) pro Quadratmeter (m²). Steradiant ist das Maß für den Raumwinkel und Quadratmeter das Maß für die Querschnittsfläche.

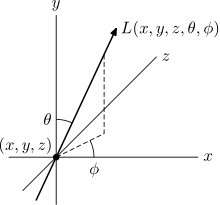
Parametrisierung eines Strahls im dreidimensionalen Raum durch Position (x,y,z) und Orientierung ( $\theta$ , $\phi$ ).

Die Verteilung der Strahldichte entlang von Lichtstrahlen in einem Bereich des dreidimensionalen Raums, die durch statische, zeitlich nicht veränderbare Lichtquellen hervorgerufen wird, bezeichnet man als plenoptische Funktion[1 3]. Die plenoptische Funktion ist eine idealisierte Funktion, die in der Bildverarbeitung und der Computergrafik genutzt wird, um ein Bild aus jeder beliebigen Position aus jedem Blickwinkel zu jedem Zeitpunkt zu beschreiben. Praktisch wird die plenoptische Funktion nicht genutzt; jedoch ist sie sinnvoll, will man verschiedene andere Konzepte der Bildverarbeitung und der Computergrafik verstehen. Da gerade Strahlen durch ihre Position in drei räumlichen Koordinaten (x, y und z) und zwei Winkel ( $\theta$ und $\phi$ ) beschrieben werden können, ist es eine fünfdimensionale Funktion. (Wellenlänge, Polarisationswinkel und die Zeit können als weitere Variablen betrachtet werden, wodurch sich eine höherdimensionale Funktion ergibt.)

Die Summierung der Strahlungsdichtevektoren

D_{1}

und

D_{2}

, die von zwei Lichtquellen

I_{1}

und

I_{2}

abgestrahlt werden, erzeugt einen resultierenden Vektor

D

mit dem dargestellten Betrag und Richtung (aus [1 4]).

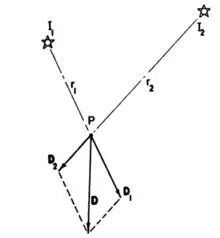
Ebenso wie Adelson (1991) definierte Gershun (1936) das Lichtfeld an jedem Punkt im Raum als eine fünfdimensionale Funktion. Er behandelte es als eine unendlich große Sammlung von Vektoren, für jede Einfallsrichtung oder Orientierung auf einen Punkt, deren Längen proportional zur Strahldichte sind. Die Integration dieser Vektoren über die gesamte Sphäre der möglichen Orientierungen an einem Punkt ergibt einen einzelnen, skalaren Wert – die Bestrahlungsstärke. Das Diagramm, das aus Gershuns Veröffentlichung reproduziert ist, zeigt diese Berechnung für den Fall von zwei Lichtquellen. In der Computergrafik wird diese „vektor-wertige“ Funktion des dreidimensionalen Raums auch als Bestrahlungsstärken-Vektorfeld bezeichnet[1 5]. Die Vektorrichtung eines Punktes im Lichtfeld kann interpretiert werden als die Normalenrichtung einer Fläche, die so auf diesem Punkt ausgerichtet wird, dass die lokale Bestrahlungsstärke dort maximal ist.

Das 4-D-Lichtfeld

Wenn in einer Szene ein konkaves Objekt vorhanden ist (z. B. der innere Teil einer gekrümmten Hand), dann wird Licht, das von einem Punkt des Objektes ausstrahlt, nach kurzer Strecke von einem anderen Punkt des Objektes blockiert. Kein praktisches Messgerät könnte die plenoptische Funktion in einer solchen Szene bestimmen.

Strahlung entlang eines Lichtstrahls bleibt konstant, sofern sie nicht durch irgendein Objekt in seiner Bahn blockiert wird.

Wenn hingegen die Szene nur auf konvexe Objekte beschränkt bleibt, dann kann die plenoptische Funktion ganz einfach (sogar mit einer Digitalkamera) bestimmt werden. Darüber hinaus enthält die Funktion in diesem Fall sogar redundante Informationen, da sich die Strahldichte entlang des Lichtstrahls nicht verändert. Die redundante Information ist genauer auf eine einzelne Dimension beschränkt, so dass eine vierdimensionale Funktion hier ausreicht. Parry Moon nannte diese 1981 Photonisches Feld[1 6], während Forscher aus dem Gebiet der Computergrafik es als 4-D-Lichtfeld[1 7] oder Lumigramm[1 8] bezeichnen. Formal ist das 4-D-Lichtfeld definiert als die Strahlungsdichte entlang Lichtstrahlen in einem leeren Raum.

Die Schar von Strahlen in einem Lichtfeld kann auf unterschiedliche Arten parametriert werden, von denen einige wenige nachfolgend gezeigt werden. Die üblicherweise genutzte Parametrierung ist die Zwei-Ebenen-Form (Bild unten, rechte Darstellung). Diese Form kann nicht alle Strahlen repräsentieren, beispielsweise keine Strahlen, die parallel zu den zwei Ebenen sind, sofern die Ebenen zueinander parallel stehen. Der Vorteil liegt allerdings darin, dass ihre Beschreibung eng verwandt ist mit der analytischen Geometrie perspektivischer Abbildung. Eine einfache Möglichkeit, sich die Zwei-Ebenen-Form des Lichtfelds vorzustellen, ist als Sammlung vieler perspektivisch abgebildeter Bilder der st-Ebene (und jedem Objekt, das darüber oder außerhalb liegt) und von denen jedes aus einer anderen Beobachtungposition in der uv-Ebene aufgenommen ist. Ein Lichtfeld, das in dieser Form parametriert ist, wird gelegentlich auch Licht-Slab genannt.

Einige alternative Formen der Parametrierung des 4-D-Lichtfelds in Bezug zum Fluss des Lichts in einem leeren Raum. Links: Punkte auf einer Ebene oder gekrümmten Oberfläche und Richtungen, die von den Punkten wegweisen. Mitte: Punktepaare auf der Oberfläche einer Kugel. Rechts: Punktepaare von Punkten auf zwei Ebenen (in jeder beliebigen Position)

Zu bemerken ist hier, dass Licht-Slab nicht meint, dass das 4-D-Lichtfeld äquivalent ist zur Erfassung zweier 2-D-Ebenen mit Informationen (letzteres ist nur zweidimensional). Zum Beispiel korrespondiert ein Punktpaar mit den Positionen (0,0) in der st-Ebene und (1,1) in der uv-Ebene mit einem Strahl im Raum; allerdings können auch andere Strahlen durch den Punkt (0,0) in der st-Ebene oder den Punkt (1,1) in der uv-Ebene fallen. Das Punktepaar hingegen beschreibt nur diesen einen Strahl, nicht alle anderen dieser Strahlen.

Analogie in der Akustik

Die Entsprechung zum 4-D-Lichtfeld in der Akustik ist das Schallfeld oder Wellenfeld, wie es in der Wellenfeldsynthese Anwendung findet. Dieses korrespondiert zum Kirchhoff-Helmholtz-Integral, das besagt, dass ohne Hindernisse im Raum das Schallfeld über der Zeit durch den Schalldruck auf einer Ebene gegeben ist. Dieses ist somit eine 2-D-Information für jeden beliebigen Punkt und, die Zeit einbeziehend, ein 3-D-Feld.

Dass das Schallfeld zwei Dimensionen besitzt (im Vergleich zum vierdimensionalen Lichtfeld), kommt daher, dass Licht in Strahlen transportiert wird (0-D an einem Raumpunkt zu einem Zeitpunkt, 1-D als Funktion der Zeit), während eine Wellenfront des Schalls wegen des huygensschen Prinzips als sphärische Wellen modelliert werden kann (2-D an einem Raumpunkt zu einem bestimmten Zeitpunkt, 3-D als Funktion der Zeit). Licht bewegt sich in einer einzigen Richtung (2-D-Information), während Schall sich in alle Richtungen ausbreitet.

Erzeugung

Lichtfelder sind fundamentale Repräsentationen für Licht. Sie können auf verschiedenen Weisen erzeugt werden, beispielsweise durch Computerprogramme oder geeignete Aufnahmetechniken.

In der Computergrafik werden Lichtfelder typischerweise durch das Rendern eines 3-D-Modells oder durch das Fotografieren einer realen Szene erzeugt. In beiden Fällen müssen Bilder aus einer großen Anzahl von unterschiedlichen Blickwinkeln aufgenommen werden, will man ein Lichtfeld schaffen. Je nach gewählter Parametrierung liegen diese Blickwinkel auf einer Linie, einer Ebene, einer Kugel oder einer anderen Geometrie. Allerdings ist auch die Wahl unstrukturierter Blickwinkel möglich[5 1].

Geräte, die Lichtfelder fotografisch aufnehmen können, bestehen aus einer bewegten, handgeführten Kamera, einer automatisch bewegten Kamera[3 1], Kameras montiert an einem Bogen (wie in dem Bullet-Time-Effekt, der aus dem Film Matrix bekannt ist), einer matrixförmigen Anordnung von Kameras[3 2][3 3][3 4] oder einer handgeführten Kamera[3 5][3 6], Mikroskop[3 7] oder einem optischen System mit einem Mikrolinsenarray, das im optischen Strahlengang positioniert ist (siehe auch plenoptische Kamera). Einige öffentliche Archive für Lichtfeld-Datensätze sind unten angegeben.

Der größte bekannte Lichtfeld-Datensatz (Michelangelo’s statue of Night) enthält 24.000 1,3-Megapixel-Bilder.[1] Die notwendige Anzahl an Bildern hängt von der Anwendung ab. Möchte man ein Lichtfeld von einem opaken Objekt rendern (siehe Abschnitt Anwendungen unten), auf daß man es von allen Seiten betrachten könne, so muss dessen Rückseite fotografiert werden. Wenn man das Objekt aus geringer Entfernung betrachten möchte und das Objekt beiderseits der st-Ebene liegt, dann müssen Bilder aus nahe beieinander liegenden Positionen in der uv-Ebene mit hoher räumlicher Auflösung aufgenommen werden (bei der oben beschriebenen Zwei-Ebenen-Parametrierung).

Die Anzahl und die Lage der Bilder in einem Lichtfeld und die Auflösung der einzelnen Bilder werden als das Sampling des 4-D-Lichtfelds bezeichnet. Von vielen Wissenschaftlern wurden Untersuchungen zum Lichtfeld-Sampling durchgeführt. Ein guter Einstiegspunkt zu diesem Thema findet sich in [2 1]. Interessant sind auch[2 2] in Bezug auf den Effekt von Verdeckung, [2 3] für den Effekt von Beleuchtung und Reflexion sowie [2 4] und[2 5] zu Anwendungen der plenoptischen Kamera und 3-D-Displays.

Anwendungen

Computational Imaging bezieht sich auf alle Methoden der Bilderzeugung, die einen Computer einbeziehen. Viele dieser Methoden arbeiten mit dem sichtbaren Wellenlängenspektrum, und viele produzieren Lichtfelder. Daher müssten nur alle Anwendungen von Computational Photography in der Kunst, der Wissenschaft, dem Ingenieurwesen und der Medizin gesucht werden, wollte man Anwendungen für Lichtfelder auflisten.

Eine nach unten weisende Lichtquelle (F-F') induziert ein Lichtfeld, dessen Strahldichtevektoren sich nach außen krümmen. Durch seine Berechnungen konnte Gershun die Strahlungsdichte berechnen, die auf einen Punkt (

P_{1},P_{2}

) einer Oberfläche fällt (aus [1 9]).

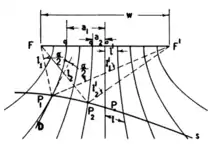
Nachfolgend sind ausgewählte Anwendungen aus dem Bereich der Computergrafik aufgeführt:

Beleuchtungs-Engineering. Gershuns Grund, das Lichtfeld zu studieren, lag darin, das Beleuchtungsmuster abzuleiten (möglichst in geschlossener Form), das oberhalb von Oberflächen auftritt und durch Lichtquellen unterschiedlicher Position und Form hervorgerufen wird. Ein Beispiel hierfür ist rechts dargestellt. Eine jüngere Untersuchung ist zum Beispiel [5 2].

Lichtfeld-Rendering. Indem 2-D-Schnitte aus einem 4-D-Lichtfeld extrahiert werden, können neue Ansichten einer Szene generiert werden[1 7][1 8]. Je nach Parametrierung des Lichtfelds können diese Ansichten perspektivisch, orthografisch, kreuzgeschlitzt[5 3], multiperspektivisch[5 4] oder gemäß einer anderen Projektionsform sein. Lichtfeld-Rendering ist eine Form des Image based Modeling and Rendering.

Fotografie mit synthetischer Apertur. Durch die Integration einer sinnvollen 4-D-Teilmenge eines Lichtfeldes kann die Ansicht approximiert werden, die entstünde, wenn das Bild mit einer Kamera mit endlicher Apertur aufgenommen werden würde. Eine solche Ansicht hat eine begrenzte Tiefenschärfe. Durch Scherung oder Krümmung des Lichtfeldes vor dieser Integration kann auf frontoparallele[5 5] oder schräge[5 6] Ebenen fokussiert werden. Wird ein Lichtfeld mit einer handgeführten Digitalkamera aufgenommen, kann der Fokus der aufgenommenen Bilder nachträglich angepasst werden[3 5] (siehe auch plenoptische Kamera).

3-D-Displays. Wird ein Lichtfeld mit einer Technik präsentiert, die jedes Sample dem entsprechenden Strahl im Raum korrekt zuordnet, so entsteht ein autostereoskopischer Effekt ähnlich wie bei der Betrachtung der realen Szene. Nichtdigitale Techniken, die dies durchführen, umfassen integrale Fotografie, Parallaxen-Panoramagramme und Holografie. Digitale Techniken für die Autostereoskopie umfassen die Nutzung von Linsenarrays über hochauflösenden Displays oder die Projektion des Bildes auf ein Linsenarray mit einem Array von Projektoren. Wird letzteres mit einem Array von Videokameras kombiniert, können zeitlich veränderliche Lichtfelder aufgenommen und projiziert werden. Mit beidem kann ein 3-D-Fernsehsystem aufgebaut werden[5 7][5 8]. Bilderzeugung und Vorverzerrung von synthetischen Bildern für holografische Stereogramme ist eines der ersten Beispiele für computergenerierte Lichtfelder, die die späteren Arbeiten von Levoy und Hanrahan motivierten[5 9][2 6].

Reduzierung von Glanzlichtern. Durch vielfache Lichtstreuung und Reflexionen innerhalb eines Objektivs treten Glanzlichter auf, die den Bildkontrast beeinträchtigen. Glanzlichter wurden bereits im zweidimensionalen Bildraum analysiert[5 10]. Es ist jedoch sinnvoll, Glanzlichter als ein Phänomen im 4-D-Strahlenraum aufzufassen[5 11]. Durch die statistische Analyse des Strahlungsraums im Inneren der Kamera können Glanzlichtartefakte klassifiziert und ausgeblendet werden. Im Strahlenraum verhalten sich Glanzlichter wie hochfrequentes Rauschen, das durch Ausreißerfilter reduziert werden kann. Eine solche Filterung kann durch die Erfassung des Lichtfelds im Inneren der Kamera durchgeführt werden; allerdings reduziert sich dabei die räumliche Auflösung des Bilds. Für die Reduzierung von Glanzlichtern ohne eine signifikante Verringerung der Auflösung könnte ein gleichförmiges/ungleichförmiges Sampling der Lichtstrahlen angewendet werden[5 11].

Quellen

Marc Levoy, Jonathan Shade: A light field of Michelangelo's statue of Night (englisch) Stanford Computer Graphics Laboratory. 25. Mai 1999. Abgerufen am 15. Juli 2019.

Theorie

Faraday, M., "Thoughts on Ray Vibrations", Philosophical Magazine, S. 3, Vol XXVIII, N188, May 1846.
Gershun, A. (1936). "The Light Field", Moscow, 1936. Translated by P. Moon and G. Timoshenko in Journal of Mathematics and Physics, Vol. XVIII, MIT, 1939, S. 51–151.
Adelson, E.H., Bergen, J.R. (1991). "The plenoptic function and the elements of early vision", In Computation Models of Visual Processing, M. Landy and J.A. Movshon, eds., MIT Press, Cambridge, 1991, pp. 3–20.
Gershun, A. (1936). "The Light Field", Moscow, 1936. Translated by P. Moon and G. Timoshenko in Journal of Mathematics and Physics, Vol. XVIII, MIT, 1939, fig 17
Arvo, J. (1994). "The Irradiance Jacobian for Partially Occluded Polyhedral Sources", Proc. ACM SIGGRAPH, ACM Press, pp. 335–342.
Moon, P., Spencer, D.E. (1981). The Photic Field, MIT Press.
Levoy, M., Hanrahan, P. (1996). "Light Field Rendering", Proc. ACM SIGGRAPH, ACM Press, pp. 31–42.
Gortler, S.J., Grzeszczuk, R., Szeliski, R., Cohen, M. (1996). "The Lumigraph", Proc. ACM SIGGRAPH, ACM Press, pp. 43–54.
Gershun, A. (1936). "The Light Field", Moscow, 1936. Translated by P. Moon and G. Timoshenko in Journal of Mathematics and Physics, Vol. XVIII, MIT, 1939, fig. 24

Wigner Distribution Function and Light Fields. (Memento vom 8. Januar 2012 im Internet Archive)

Analyse

Chai, J.-X., Tong, X., Chan, S.-C., Shum, H. (2000). "Plenoptic Sampling", Proc. ACM SIGGRAPH, ACM Press, pp. 307–318.
Durand, F., Holzschuch, N., Soler, C., Chan, E., Sillion, F. X. (2005). "A Frequency analysis of Light Transport", Proc. ACM SIGGRAPH, ACM Press, pp. 1115–1126.
Ramamoorthi, R., Mahajan, D., Belhumeur, P. (2006). "A First Order Analysis of Lighting, Shading, and Shadows" (Memento des Originals vom 28. August 2006 im Internet Archive) Info: Der Archivlink wurde automatisch eingesetzt und noch nicht geprüft. Bitte prüfe Original- und Archivlink gemäß Anleitung und entferne dann diesen Hinweis.@1@2, ACM TOG.
Ng, R. (2005). "Fourier Slice Photography", Proc. ACM SIGGRAPH, ACM Press, pp. 735–744.
Zwicker, M., Matusik, W., Durand, F., Pfister, H. (2006). "Antialiasing for Automultiscopic 3D Displays" (Memento des Originals vom 1. Mai 2007 im Internet Archive) Info: Der Archivlink wurde automatisch eingesetzt und noch nicht geprüft. Bitte prüfe Original- und Archivlink gemäß Anleitung und entferne dann diesen Hinweis.@1@2, Eurographics Symposium on Rendering, 2006.
Halle, M. (1994) "Holographic stereograms as discrete imaging systems" (PDF; 992 kB), In: SPIE Proc. Vol. #2176: Practical Holography VIII, S.A. Benton, ed., pp. 73–84.

Geräte

Levoy, M. (2002). Stanford Spherical Gantry.
Kanade, T., Saito, H., Vedula, S. (1998). "The 3D Room: Digitizing Time-Varying 3D Events by Synchronized Multiple Video Streams", Tech report CMU-RI-TR-98-34, December 1998.
Yang, J.C., Everett, M., Buehler, C., McMillan, L. (2002). "A real-time distributed light field camera", Proc. Eurographics Rendering Workshop 2002.
Wilburn, B., Joshi, N., Vaish, V., Talvala, E., Antunez, E., Barth, A., Adams, A., Levoy, M., Horowitz, M. (2005). "High Performance Imaging Using Large Camera Arrays", ACM Transactions on Graphics (Proc. SIGGRAPH), Vol. 24, No. 3, pp. 765–776.
Ng, R., Levoy, M., Brédif, M., Duval, G., Horowitz, M., Hanrahan, P. (2005). "Light Field Photography with a Hand-Held Plenoptic Camera", Stanford Tech Report CTSR 2005-02, April, 2005.
Georgiev, T., Zheng, C., Nayar, S., Curless, B., Salesin, D., Intwala, C. (2006). "Spatio-angular Resolution Trade-offs in Integral Photography" (PDF; 593 kB), Proc. EGSR 2006.
Levoy, M., Ng, R., Adams, A., Footer, M., Horowitz, M. (2006). "Light field microscopy", ACM Transactions on Graphics (Proc. SIGGRAPH), Vol. 25, No. 3.

C.K. Liang, T.H. Lin, B.Y. Wong, C. Liu, H. H. Chen: Programmable Aperture Photography: Multiplexed Light Field Acquisition. Proc. ACM SIGGRAPH. 2008.
A. Veeraraghavan, R. Raskar, A. Agrawal, A. Mohan, J. Tumblin: Dappled Photography: Mask Enhanced Cameras for Heterodyned Light Fields and Coded Aperture Refocusing. Proc. ACM SIGGRAPH. 2007.

Lichtfeldarchive

Anwendungen

Buehler, C., Bosse, M., McMillan, L., Gortler, S., Cohen, M. (2001). "Unstructured Lumigraph rendering", Proc. ACM SIGGRAPH, ACM Press.
Ashdown, I. (1993). "Near-Field Photometry: A New Approach", Journal of the Illuminating Engineering Society, Vol. 22, No. 1, Winter, 1993, S. 163–180.
Zomet, A., Feldman, D., Peleg, S., Weinshall, D. (2003). "Mosaicing new views: the crossed-slits projection", IEEE Transactions on Pattern Analysis and Machine Intelligence (PAMI), Vol. 25, No. 6, June 2003, pp. 741–754.
Rademacher, P., Bishop, G. (1998). "Multiple-Center-of-Projection Images", Proc. ACM SIGGRAPH, ACM Press.
Isaksen, A., McMillan, L., Gortler, S.J. (2000). "Dynamically Reparameterized Light Fields", Proc. ACM SIGGRAPH, ACM Press, pp. 297–306.
Vaish, V., Garg, G., Talvala, E., Antunez, E., Wilburn, B., Horowitz, M., Levoy, M. (2005). "Synthetic Aperture Focusing using a Shear-Warp Factorization of the Viewing Transform", Proc. Workshop on Advanced 3D Imaging for Safety and Security, in conjunction with CVPR 2005.
Javidi, B., Okano, F., eds. (2002). Three-Dimensional Television, Video and Display Technologies, Springer-Verlag.
Matusik, W., Pfister, H. (2004). "3D TV: a scalable system for real-time acquisition, transmission, and autostereoscopic display of dynamic scenes", Proc. ACM SIGGRAPH, ACM Press.
Halle, M., Benton, S., Klug, M., Underkoffler, J. (1991). "The UltraGram: a generalized holographic stereogram" (PDF; 320 kB), SPIE Vol. 1461, Practical Holography V, S.A. Benton, ed., pp. 142–155.
Talvala, E-V., Adams, A., Horowitz, M., Levoy, M. (2007). "Veiling glare in high dynamic range imaging", Proc. ACM SIGGRAPH.
Raskar, R., Agrawal, A., Wilson, C., Veeraraghavan, A. (2008). "Glare Aware Photography: 4D Ray Sampling for Reducing Glare Effects of Camera Lenses", Proc. ACM SIGGRAPH.

F. Pérez, J. G. Marichal, J. M. Rodriguez: The Discrete Focal Stack Transform. (PDF; 869 kB) Proc. EUSIPCO 2008.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[17] Marc Levoy, Jonathan Shade: A light field of Michelangelo's statue of Night (englisch) Stanford Computer Graphics Laboratory. 25. Mai 1999. Abgerufen am 15. Juli 2019.

[1] Faraday, M., "Thoughts on Ray Vibrations", Philosophical Magazine, S. 3, Vol XXVIII, N188, May 1846.

[2] Gershun, A. (1936). "The Light Field", Moscow, 1936. Translated by P. Moon and G. Timoshenko in Journal of Mathematics and Physics, Vol. XVIII, MIT, 1939, S. 51–151.

[3] Adelson, E.H., Bergen, J.R. (1991). "The plenoptic function and the elements of early vision", In Computation Models of Visual Processing, M. Landy and J.A. Movshon, eds., MIT Press, Cambridge, 1991, pp. 3–20.

[4] Gershun, A. (1936). "The Light Field", Moscow, 1936. Translated by P. Moon and G. Timoshenko in Journal of Mathematics and Physics, Vol. XVIII, MIT, 1939, fig 17

[5] Arvo, J. (1994). "The Irradiance Jacobian for Partially Occluded Polyhedral Sources", Proc. ACM SIGGRAPH, ACM Press, pp. 335–342.

[6] Moon, P., Spencer, D.E. (1981). The Photic Field, MIT Press.

[Levoy_1996-7] Levoy, M., Hanrahan, P. (1996). "Light Field Rendering", Proc. ACM SIGGRAPH, ACM Press, pp. 31–42.

[Gortler_1996-8] Gortler, S.J., Grzeszczuk, R., Szeliski, R., Cohen, M. (1996). "The Lumigraph", Proc. ACM SIGGRAPH, ACM Press, pp. 43–54.

[23] Gershun, A. (1936). "The Light Field", Moscow, 1936. Translated by P. Moon and G. Timoshenko in Journal of Mathematics and Physics, Vol. XVIII, MIT, 1939, fig. 24

[18] Chai, J.-X., Tong, X., Chan, S.-C., Shum, H. (2000). "Plenoptic Sampling", Proc. ACM SIGGRAPH, ACM Press, pp. 307–318.

[19] Durand, F., Holzschuch, N., Soler, C., Chan, E., Sillion, F. X. (2005). "A Frequency analysis of Light Transport", Proc. ACM SIGGRAPH, ACM Press, pp. 1115–1126.

[20] Ramamoorthi, R., Mahajan, D., Belhumeur, P. (2006). "A First Order Analysis of Lighting, Shading, and Shadows" (Memento des Originals vom 28. August 2006 im Internet Archive) Info: Der Archivlink wurde automatisch eingesetzt und noch nicht geprüft. Bitte prüfe Original- und Archivlink gemäß Anleitung und entferne dann diesen Hinweis.@1@2, ACM TOG.

[21] Ng, R. (2005). "Fourier Slice Photography", Proc. ACM SIGGRAPH, ACM Press, pp. 735–744.

[22] Zwicker, M., Matusik, W., Durand, F., Pfister, H. (2006). "Antialiasing for Automultiscopic 3D Displays" (Memento des Originals vom 1. Mai 2007 im Internet Archive) Info: Der Archivlink wurde automatisch eingesetzt und noch nicht geprüft. Bitte prüfe Original- und Archivlink gemäß Anleitung und entferne dann diesen Hinweis.@1@2, Eurographics Symposium on Rendering, 2006.

[32] Halle, M. (1994) "Holographic stereograms as discrete imaging systems" (PDF; 992 kB), In: SPIE Proc. Vol. #2176: Practical Holography VIII, S.A. Benton, ed., pp. 73–84.

[10] Levoy, M. (2002). Stanford Spherical Gantry.

[11] Kanade, T., Saito, H., Vedula, S. (1998). "The 3D Room: Digitizing Time-Varying 3D Events by Synchronized Multiple Video Streams", Tech report CMU-RI-TR-98-34, December 1998.

[12] Yang, J.C., Everett, M., Buehler, C., McMillan, L. (2002). "A real-time distributed light field camera", Proc. Eurographics Rendering Workshop 2002.

[13] Wilburn, B., Joshi, N., Vaish, V., Talvala, E., Antunez, E., Barth, A., Adams, A., Levoy, M., Horowitz, M. (2005). "High Performance Imaging Using Large Camera Arrays", ACM Transactions on Graphics (Proc. SIGGRAPH), Vol. 24, No. 3, pp. 765–776.

[NG_2005-14] Ng, R., Levoy, M., Brédif, M., Duval, G., Horowitz, M., Hanrahan, P. (2005). "Light Field Photography with a Hand-Held Plenoptic Camera", Stanford Tech Report CTSR 2005-02, April, 2005.

[15] Georgiev, T., Zheng, C., Nayar, S., Curless, B., Salesin, D., Intwala, C. (2006). "Spatio-angular Resolution Trade-offs in Integral Photography" (PDF; 593 kB), Proc. EGSR 2006.

[16] Levoy, M., Ng, R., Adams, A., Footer, M., Horowitz, M. (2006). "Light field microscopy", ACM Transactions on Graphics (Proc. SIGGRAPH), Vol. 25, No. 3.

[9] Buehler, C., Bosse, M., McMillan, L., Gortler, S., Cohen, M. (2001). "Unstructured Lumigraph rendering", Proc. ACM SIGGRAPH, ACM Press.

[24] Ashdown, I. (1993). "Near-Field Photometry: A New Approach", Journal of the Illuminating Engineering Society, Vol. 22, No. 1, Winter, 1993, S. 163–180.

[25] Zomet, A., Feldman, D., Peleg, S., Weinshall, D. (2003). "Mosaicing new views: the crossed-slits projection", IEEE Transactions on Pattern Analysis and Machine Intelligence (PAMI), Vol. 25, No. 6, June 2003, pp. 741–754.

[26] Rademacher, P., Bishop, G. (1998). "Multiple-Center-of-Projection Images", Proc. ACM SIGGRAPH, ACM Press.

[27] Isaksen, A., McMillan, L., Gortler, S.J. (2000). "Dynamically Reparameterized Light Fields", Proc. ACM SIGGRAPH, ACM Press, pp. 297–306.

[28] Vaish, V., Garg, G., Talvala, E., Antunez, E., Wilburn, B., Horowitz, M., Levoy, M. (2005). "Synthetic Aperture Focusing using a Shear-Warp Factorization of the Viewing Transform", Proc. Workshop on Advanced 3D Imaging for Safety and Security, in conjunction with CVPR 2005.

[29] Javidi, B., Okano, F., eds. (2002). Three-Dimensional Television, Video and Display Technologies, Springer-Verlag.

[30] Matusik, W., Pfister, H. (2004). "3D TV: a scalable system for real-time acquisition, transmission, and autostereoscopic display of dynamic scenes", Proc. ACM SIGGRAPH, ACM Press.

[31] Halle, M., Benton, S., Klug, M., Underkoffler, J. (1991). "The UltraGram: a generalized holographic stereogram" (PDF; 320 kB), SPIE Vol. 1461, Practical Holography V, S.A. Benton, ed., pp. 142–155.

[33] Talvala, E-V., Adams, A., Horowitz, M., Levoy, M. (2007). "Veiling glare in high dynamic range imaging", Proc. ACM SIGGRAPH.

[Raskar_2008-34] Raskar, R., Agrawal, A., Wilson, C., Veeraraghavan, A. (2008). "Glare Aware Photography: 4D Ray Sampling for Reducing Glare Effects of Camera Lenses", Proc. ACM SIGGRAPH.