Kräftesystem

Das Kräftesystem (auch Kraftsystem oder Kraft-/Kräftegruppe) ist ein Begriff aus der Mechanik, der ein System von mechanischen Wechselwirkungen zwischen Körpern bezeichnet. Bei der Analyse von Kräftesystemen kann es darum gehen, unbekannte Kräfte im System zu berechnen, das Kräftesystem in ein einfacheres, gleichwertiges zu überführen, was weitere Analysen erleichtert, oder die durch die Kräfte bewirkten Beschleunigungen der beteiligten Körper zu ermitteln. Die Analyse allgemeiner Kräftesysteme ist ohne den Begriff des Drehmoments nicht möglich.

Im Maschinenbau und in der Baustatik ist die Kenntnis der Belastungen für die Dimensionierung von Objekten unabdingbar. Zur Auslegung von Fahrwerken beispielsweise werden die Kräftesysteme in den verschiedenen Bewegungszuständen durch Mehrkörpersimulation berechnet, was dann die fahrdynamischen Eigenschaften und die Belastungen des Fahrwerks zu bewerten gestattet.

Innere, äußere und Reaktionskräfte

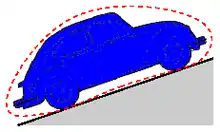
Abb. 1: Freischnitt (rot) eines am Hang (grau) fahrenden Autos (blau)

Kräfte sind nach dem Prinzip Actio und Reactio immer Wechselwirkungen zwischen Körpern, in Abb. 1 zwischen Hang und Auto. Übt ein Körpern K₁ auf den anderen K₂ eine Kraft F aus, dann tut dies der andere auch auf ersteren:

${\stackrel {K_{1}}{\square }}\,{\stackrel {F}{\leftarrow }}\quad {\stackrel {F}{\rightarrow }}\,{\stackrel {K_{2}}{\square }}$

Beide Kräfte haben dieselbe Wirkungslinie und sind entgegengesetzt gleich groß. Kräfte können bei Kontakt oder berührungslos durch Massenanziehung und Magnetismus ausgeübt werden. Die Kräfte zwischen zum System gehörenden Körpern werden innere Kräfte genannt und heben sich in der Summe sämtlich gegenseitig auf. Daneben gibt es Wechselwirkungen zwischen Körpern, die zum System gehören, und solchen die nicht zum System gehören. Dies sind von außen angreifende oder äußere Kräfte und sie treten im System immer nur einfach auf, beispielsweise als Zwangskraft oder eingeprägte Kraft.

Körper können durch die Kraftwirkung ihren Bewegungszustand ändern und/oder sich verformen. Zur Ermittlung der Kräfte wird der Körper aus seiner Umgebung freigeschnitten. Die Schnittführung muss immer am Originalsystem erfolgen und so wie in Abb. 1 geschlossen sein.

Definition, Lageplan und Kräfteplan

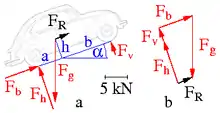
Abb. 2: a: Lageplan für ein bergauf fahrendes Auto (grau) mit äußeren Kräften (rot) und Maßen (blau), b: Kräfteplan

Da Kräfte auch Drehmomente verursachen, ist ein Kräftesystem KS erst durch Angabe aller (n) Kräfte ${\vec {F}}_{1,...,n}$ zusammen mit ihren Kraftangriffspunkten ${\vec {r}}_{1,...,n}$ eindeutig festgelegt:

KS:=\{({\vec {F}}_{i},{\vec {r}}_{i}),i=1,\ldots ,n\}

Im maßstäblichen Lageplan werden die Kräfte so eingezeichnet, wie sie im System angreifen, siehe Abb. 2. Der Lageplan entspricht einem maßstäblichen Freikörperbild des Systems. Im Kräfteplan werden die Kräfte mittels eines Maßstabs mit der Dimension Länge pro Krafteinheit graphisch zum Kräftepolygon zusammengesetzt. Die im Kräfteplan ermittelte resultierende Kraft F_R wird in den Lageplan übertragen. Weil diese im Bild hangaufwärts weist, wird das Auto beschleunigen.

Grundaufgaben der Statik

Die Grundaufgaben der Statik sind die Reduktion auf eine resultierende Kraft und ein resultierendes Moment, Bestimmung des Gleichgewichts von Kräftesystemen und die Zerlegung einer Kraft.

Bei der Reduktion geht es darum, ein Kräftesystem rechnerisch oder graphisch zu vereinfachen. Es zeigt sich, dass jedes Kräftesystem in seiner Wirkung auf einen starren Körper äquivalent ist zu einer resultierenden Kraft mit einem bestimmten Angriffspunkt und einem resultierenden Moment:

\sum _{i=1}^{n}{\vec {F}}_{i}={\vec {F}}_{R}\quad {\text{und}}\quad \sum _{i=1}^{n}({\vec {r}}_{i}-{\vec {c}})\times {\vec {F}}_{i}={\vec {M}}_{cR}.

Die resultierende Kraft und das resultierende Moment bilden zusammen die Dyname.

Ein Körper ist im Gleichgewicht, wenn er in Ruhe verharrt oder seinen Bewegungszustand beibehält, was Bedingungen an das an ihm angreifende Kräftesystem stellt: In einem Gleichgewichtssystem verschwinden die resultierende Kraft und das resultierende Moment. Früher[1] wurde dies erster und zweiter Hauptsatz der Statik starrer Körper genannt. Ein Kräftesystem, das einen Körper im Gleichgewicht belässt, ist ein „Gleichgewichtssystem“ oder eine „Gleichgewichtsgruppe.“ Solche Systeme ändern das Gleichgewicht oder die Wirkung des Kräftesystems auf einen starren Körper nicht und dürfen entsprechend zu einem Kräftesystem hinzugefügt oder aus ihm entfernt werden.

Die Zerlegung von Kräften ist der umgekehrte Vorgang zur Bestimmung der Resultierenden. Eine Kraft wird zerlegt in Komponenten, deren Resultierende die Kraft selbst ist. Praktisch ist die Zerlegung in paarweise zueinander senkrechte Komponenten, was analytisch auf die Darstellung des Kraftvektors bezüglich einer Orthonormalbasis hinaus läuft.

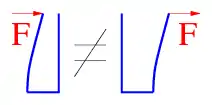
Abb. 3: Für das Gleichgewicht sind beide auf den blauen Drahtbügel wirkenden Kräfte (rot) gleichbedeutend, nicht so für die Deformation

Nur für die Analyse der Wirkung auf starre Körper oder Gleichgewichtsbetrachtungen an deformierbaren Körpern dürfen Kräfte gedanklich hinzugefügt, abgezogen oder verschoben werden. Wenn die Schnittreaktionen und die Deformation von Körpern aufgrund der eingeprägten Kräfte interessieren, dann dürfen die Kräfte nicht verändert werden, siehe Abb. 3. Nur das Zerlegen in Komponenten oder das Zusammenfassen in einem Punkt angreifender Kräfte zu einer Resultierenden, siehe unten, ist immer statthaft.

Statische Äquivalenz

Zwei Kräftesysteme, die an einem Starrkörper angreifen, sind statisch äquivalent, wenn sie bei beliebigen Starrkörperbewegungen der Kraftangriffspunkte die gleiche Leistung erbringen[2]. Die Leistungen einer Kraft ${\vec {F}}$ und eines Moments ${\vec {M}}$ sind:

L_{F}:={\vec {F}}\cdot {\vec {v}}\quad {\text{bzw.}}\quad L_{M}:={\vec {M}}\cdot {\vec {\omega }}

Darin ist ${\vec {v}}$ die Geschwindigkeit des Kraftangriffspunkts am Starrkörper und ${\vec {\omega }}$ die Winkelgeschwindigkeit des Starrkörpers. Die Idee hinter dieser Definition ist, dass wenn sich ein ruhender Körper irgendwie in Bewegung setzt, beispielsweise weil ein Lager versagt, an ihn angreifende Kräftesysteme statisch äquivalent sind, wenn jedes System bei jeder solchen hypothetischen Bewegung dieselbe Energie pro Zeiteinheit (Leistung) in den Körper einbringt. Die in der Technik weit verbreitete Annahme kleiner Verformungen eines Körpers beinhaltet, dass seine Bewegungen zumindest anfänglich Starrkörperbewegungen sind.

Es zeigt sich: Zwei Kräftesysteme sind genau dann statisch äquivalent, wenn ihre resultierende Kraft und ihr resultierendes Moment bezüglich eines beliebigen Bezugspunkts gleich sind.

Analytisch heißt das, dass die Kräftesysteme

KS^{a}:=\{({\vec {F}}_{i}^{a},{\vec {r}}_{i}^{a}),i=1,\ldots ,n\}\quad {\text{und}}\quad KS^{b}:=\{({\vec {F}}_{i}^{b},{\vec {r}}_{i}^{b}),i=1,\ldots ,m\}

genau dann statisch äquivalent sind, wenn für jeden Bezugspunkt ${\vec {c}}$ gilt:

\sum _{i=1}^{n}{\vec {F}}_{i}^{a}=\sum _{i=1}^{m}{\vec {F}}_{i}^{b}\quad {\text{und}}\quad \sum _{i=1}^{n}({\vec {r}}_{i}^{a}-{\vec {c}})\times {\vec {F}}_{i}^{a}=\sum _{i=1}^{m}({\vec {r}}_{i}^{b}-{\vec {c}})\times {\vec {F}}_{i}^{b}

Früher[1] wurde dies dritter Hauptsatz der Statik starrer Körper genannt.

Bearbeitung von Kräftesystemen

Mit den in diesem Abschnitt vorgestellten anschaulichen Verfahren können Kräftesysteme graphisch in andere besser überblickbare Kräftesysteme überführt werden.

Einzelkraft

Eine Einzelkraft ist das denkbar einfachste Kräftesystem, das aus einer Kraft mit Betrag und Richtung und dem Kraftangriffspunkt besteht. Der Angriffspunkt und die Richtung der Kraft bestimmt ihre Wirkungslinie, auf der die Kraft verschoben werden kann, ohne dass sich ihre Wirkung auf einen Starrkörper ändern würde. Die Kraft ist damit ein gebundener Vektor.

Kräfteparallelogramm

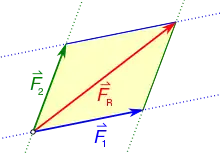
Abb. 4: Kräfteparallelogramm aus zwei Kräften (grün und blau) und ihrer Resultierenden (rot)

Zwei am selben Punkt angreifende Kräfte können durch eine Resultierende ersetzt werden, siehe Abb. 4. Die Kräfte bilden zwei Seiten eines Parallelogramms (gelblich) und die resultierende Kraft ist die Diagonale des Parallelogramms (rot). Diese graphische Konstruktion entspricht analytisch der Addition der die Kräfte repräsentierenden Vektoren.

Der umgekehrte Weg wird bei der Zerlegung einer Kraft in Komponenten beschritten, die parallel zu einer gewählten Vektorraumbasis wirken und die in der Summe die Kraft selbst ergeben. Die Komponenten der Kraft sind dann analytisch die Komponenten ihres Vektors bezüglich der gewählten Basis.

Ungleiche, parallele Kräfte

Auch zwei auf verschiedenen aber parallelen Wirkungslinien arbeitende Kräfte, die nicht entgegengesetzt gleich groß sind, können in ihrer Wirkung auf einen Starrkörper durch eine Resultierende ersetzt werden, siehe Abb. 5.

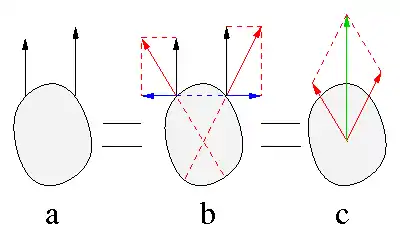
Abb. 5: Konstruktion der Resultierenden (c, grün) zu zwei ungleichen, parallelen Kräften (a, schwarz) mit Hilfe einer Nullkraft (b, blau)

Dazu wird eine Gleichgewichtsgruppe aus zwei sich auslöschenden, entgegengesetzt gleich großen Kräften mit identischer Wirkungslinie hinzugefügt (blau in Abb.5b). Die Resultierenden aus den ursprünglichen Kräften und je einer der hinzugefügten bilden ein zentrales Kräftesystem (rot) und können durch die Resultierende im Schnittpunkt ihrer Wirkungslinien ersetzt werden (grün in Abb. 5c).

Kräftepaar und Drehmoment

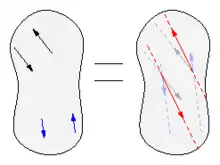
Abb. 6: Zwei Kräftepaare (blau und schwarz) entsprechen einem resultierenden Kräftepaar (rot)

Ein Kräftepaar ist ein Kräftesystem, das aus zwei entgegengesetzt gleich großen Kräften F besteht, deren Wirkungslinien gemäß dem Schema

F\uparrow \;\longleftarrow a\longrightarrow \;\downarrow F

in einem Abstand a parallel verlaufen. Die Summe der beiden Kräfte ist zwar der Nullvektor, aber die Kräfte bewirken ein Moment M, das senkrecht zu der Ebene, die von den beiden Wirkungslinien definiert wird, arbeitet und betraglich gleich dem Produkt aus dem Abstand zwischen den Wirkungslinien und einer der Kräfte ist:

M = a · F.

Ein Kräftepaar ist in seiner Wirkung auf einen Starrkörper zu diesem Moment gleichwertig. Das Kräftepaar ist nicht durch eine resultierende Kraft ersetzbar. Das Kräftepaar hat das Bestreben einen Körper zu drehen und ist daher kein Gleichgewichtssystem.

Wie bei Kräften kann, wie in Abb. 6 angedeutet, auch ein resultierendes Kräftepaar konstruiert werden, indem aus den Partnern (schwarz und blau) die Resultierenden (rot) bestimmt werden, die das resultierende Kräftepaar bilden. Diese Tatsache wird Momentensatz oder erster Varignon'scher Satz von Pierre de Varignon genannt.

Ein Kräftepaar kann frei im Raum verschoben werden, ohne dass sich seine Wirkung auf einen Starrkörper ändern würde, siehe Abb. 7.

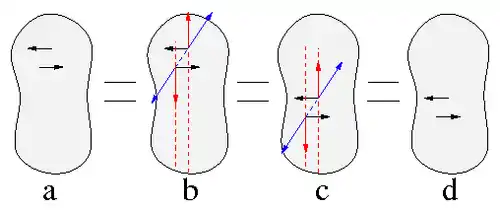
Abb. 7: Ein Kräftepaar (schwarz) kann beliebig im Raum parallel verschoben werden.

Dazu wird am Kräftepaar (schwarz in 7a,b) eine Gleichgewichtsgruppe (blau in 7b) angetragen. Die Resultierenden (rot in 7b) können entlang ihrer Wirkungslinien (gestrichelt in 7b,c) verschoben werden. Zerlegung der Resultierenden in eine Gleichgewichtsgruppe (blau in 7c) und das verschobene Kräftepaar (schwarz in 7cd) zeigt, dass die Kräftesysteme in Abb. 7a und d äquivalent sind. Mit dem Kräftepaar ist auch das entsprechende Drehmoment frei verschiebbar, was auch zweiter Varignon'scher Satz genannt wird.[3] Der Angriffspunkt kann bei Drehmomenten frei gewählt werden, sie sind freie Vektoren.

Versetzungs- oder Versatzmoment

Eine Kraft darf entlang ihrer Wirkungslinie verschoben werden, ohne dass sich dabei ihre Wirkung auf einen starren Körper ändern würde. Bei der Parallelverschiebung quer zur Wirkungslinie entsteht ein Versetzungs- oder Versatzmoment, siehe Abb. 8.

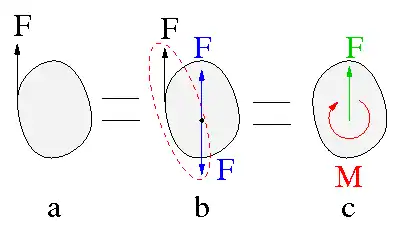
Abb. 8:Eine Einzelkraft (a, schwarz) ist äquivalent zu einer versetzten Kraft (c, grün) und einem Versetzungsmoment (c, rot).

Durch Hinzufügung eines Gleichgewichtssystems aus Kraft und entgegengesetzt gleichgroßer, auslöschender Kraft (blau in Abb. 8b) entsteht ein gleichwertiges System aus der versetzten Kraft (grün in Abb. 8c) mit Versetzungsmoment (rot in Abb. 8c).

Kraftschraube oder -winder

Mit Hilfe des Versatzmoments kann ein Kräftesystem aus einer Kraft ${\vec {F}}$ und einem beliebigen Moment ${\vec {M}}$ überführt werden in ein statisch äquivalentes Kräftesystem aus einer betraglich gleichen, parallelverschobenen Kraft ${\vec {F}}_{\parallel }$ und einem Moment ${\vec {M}}_{\parallel }$ , das zur Kraft parallel ist, siehe Abb. 9.

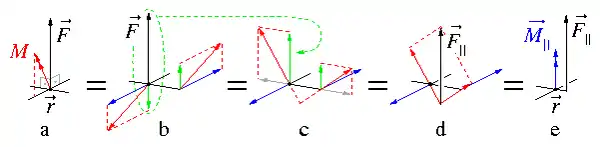
Abb. 9: Aus beliebiger Kraft und Moment wird eine versetzte Kraft und ein dazu paralleles Moment. Genaue Beschreibung erfolgt im Text.

Dazu wird das Moment in ein Kräftepaar überführt (rot in 9b), das zerlegt wird in ein Kräftepaar mit Kraftkomponenten senkrecht zur Kraft (blau) und parallel zur Kraft (grün). Aus letzterem Kräftepaar resultiert zusammen mit der Kraft ${\vec {F}}$ ein Kraftsystem aus zwei parallelen Kräften (grün in 9c), aus dem mit oben dargestellten Mitteln die Resultierende ${\vec {F}}_{\parallel }$ konstruiert wird. Diese ist betraglich gleich der ursprünglichen Kraft aber parallelverschoben. Das Kräftepaar mit den zu ${\vec {F}}$ senkrechten Kräften erzeugt ein Moment, das parallel ist zu ${\vec {F}}$ (blau in 9e). Das System aus der parallelverschobenen Kraft und dem dazu parallelen Moment ist statisch äquivalent zum ursprünglichen Kräftesystem und wird Kraftwinder oder Kraftschraube genannt, die ein wichtiger Begriff in der Schraubentheorie ist.

Spezielle Kräftesysteme

Allgemeine und räumliche Kräftesysteme

Beim allgemeinen Kräftesystem arbeiten die Kräfte auf beliebigen Wirkungslinien, die sich nicht alle in einem Punkt treffen müssen. Allgemeine Kräftesysteme sind im Allgemeinen also nicht zentral. Sie können räumlich oder eben, im Gleichgewicht sein oder nicht.

In räumlichen Kräftesystemen arbeiten die Kräfte in beliebigen Raumrichtungen. Räumliche Kräftesysteme sind im Allgemeinen also nicht eben. Sie können aber allgemein oder zentral und im Gleichgewicht sein oder nicht.

Ebenes Kräftesystem

Im ebenen Kräftesystem liegen die Wirkungslinien der Kräfte alle in einer gemeinsamen Ebene. Ebene Kräftesysteme können graphisch besonders anschaulich bearbeitet werden, wobei die oben vorgestellten Methoden angewendet werden. Bei vielen Kräften bietet sich das Seileckverfahren an, um die Resultierende zu bestimmen.

Zentrales Kräftesystem

Ein zentrales Kräftesystem besteht aus Kräften, deren Wirkungslinien alle durch einen Punkt P gehen. Das Kräfteparallelogramm ist ein einfaches zentrales Kräftesystem. Die resultierende Kraft ist die Summe der Kräfte und diese ist in ihrer Wirkung auf einen starren Körper äquivalent zum zentralen Kräftesystem. Bezüglich des Punkts P tritt kein Drehmoment auf. Die sich paarweise auslöschenden inneren Kräfte bilden besonders einfache zentrale Kräftesysteme mit verschwindender Resultierenden, die jederzeit und überall hinzugefügt oder entfernt werden dürfen, ohne dass dies Körper irgendwie beeinflussen würde. Das zentrale Kräftesystem ist ein Gleichgewichtssystem, wenn die resultierende Kraft verschwindet.

Gleichgewichtssystem

Ein Kräftesystem ist im Gleichgewicht, wenn sowohl die resultierende Kraft als auch das resultierende Moment in einem Bezugspunkt verschwinden. Gleichwertig sind in der Starrkörpermechanik die Aussagen, es wirken keine Resultierenden oder das Kräftesystem ist statisch äquivalent zu einem System, in dem keine Kräfte wirken.

Graphisch werden die Resultierenden ermittelt, indem die Kräfte entlang ihrer Wirkungslinien in den Bezugspunkt, gegebenenfalls unter Einbringung eines Versetzungsmoments, verschoben werden. So entsteht im Bezugspunkt eine resultierende Kraft und ein resultierendes Moment, und wenn beide der Nullvektor sind, dann ist das System im Gleichgewicht. Durch günstige Wahl des Bezugspunkts lässt sich die Analyse oft vereinfachen.

Analytisch leiten sich sechs linear unabhängige Gleichgewichtsbedingungen für die Komponenten der resultierenden Kraft (Kräftegleichgewicht) und des resultierenden Moments (Momentengleichgewicht) bezüglich eines Punkts ${\vec {s}}$ ab:

{\vec {F}}_{R}:=\sum _{i=1}^{n}{\vec {F}}_{i}={\vec {0}}\quad {\text{und}}\quad {\vec {M}}_{sR}:=\sum _{i=1}^{n}({\vec {r}}_{i}-{\vec {s}})\times {\vec {F}}_{i}={\vec {0}}.

Sind die Kräfte und Momente bezüglich eines Punkts ${\vec {s}}$ im Gleichgewicht, dann verschwindet ihre Momentenresultierende auch bezüglich jedes anderen Bezugspunkts ${\vec {c}}$ . Denn mit obigen Gleichgewichtsbedingungen folgt:

{\begin{aligned}{\vec {M}}_{cR}:=&\sum _{i=1}^{n}({\vec {r}}_{i}-{\vec {c}})\times {\vec {F}}_{i}=\sum _{i=1}^{n}({\vec {r}}_{i}-{\vec {s}}+{\vec {s}}-{\vec {c}})\times {\vec {F}}_{i}\\=&\sum _{i=1}^{n}({\vec {r}}_{i}-{\vec {s}})\times {\vec {F}}_{i}+({\vec {s}}-{\vec {c}})\times \sum _{i=1}^{n}{\vec {F}}_{i}={\vec {M}}_{sR}+({\vec {s}}-{\vec {c}})\times {\vec {F}}_{R}={\vec {0}}.\end{aligned}}

Ein Gleichgewichtssystem kann zu einem anderen Kräftesystem hinzugefügt werden, ohne es in seinem Gleichgewicht zu stören. Wenn jedes seiner Teilsysteme im Gleichgewicht ist, dann ist auch das Gesamtsystem im Gleichgewicht.

Anwendung in der Starrkörpermechanik

Jedes Kräftesystem kann in seiner Wirkung auf einen starren Körper durch eine in seinem Massenmittelpunkt angreifende resultierende Kraft und ein resultierendes Drehmoment ersetzt werden. Das Gesetz „Kraft gleich Masse mal Beschleunigung“ und die Euler’schen Kreiselgleichungen liefern dann sechs Differentialgleichungen, mit denen die Bewegung des Systems bestimmt werden, siehe Mehrkörpersimulation.

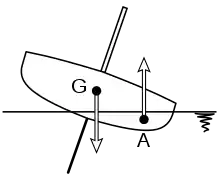
Die Stabilitätstheorie beschäftigt sich mit der Frage, ob eine kleine Lageänderung des Körpers durch das äußere Kräftesystem angefacht oder gedämpft wird, was beispielsweise bei Schiffskörpern interessiert, siehe Bild. Das Kraftsystem aus Auftriebskraft A und Gewichtskraft G versucht die Jolle wieder in die aufrechte Lage zu bringen: Der Schiffskörper ist formstabil.

Anwendung in der Festigkeitslehre

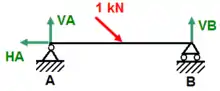
In der Festigkeitslehre interessieren die Belastungen der Körper, an denen das Kräftesystem angreift. An deformierbaren Körpern dürfen Kraftangriffspunkte nicht versetzt werden. Aus den Gleichgewichtsbedingungen können in statisch bestimmt gelagerten Körpern, wie im Bild, aus den bekannten eingeprägten Kräften eventuell noch unbekannte Auflagerreaktionen (grün) ausgerechnet werden. Dann liegen alle äußeren Kräfte vor und innere Schnittreaktionen können an beliebiger Stelle ermittelt werden. Materialannahmen, von denen die der linearen Elastizität die einfachste ist, gestatten es, auf die Beanspruchung des Körpers am Ort der Schnittreaktionen zu schließen und so eine Grundlage für die Dimensionierung der Körper zu liefern.

Siehe auch

Polplan

Einzelnachweise

H. Egerer: Ingenieur-Mechanik. Lehrbuch der technischen Mechanik in vorwiegend graphischer Behandlung. Band 1. Springer, Berlin, Heidelberg 1919, ISBN 978-3-662-32061-7, S. 124 (google.de [abgerufen am 3. Januar 2017]).
M. B. Sayir, J. Dual, S. Kaufmann: Ingenieurmechanik 1. Grundlagen und Statik. Springer, 2008, ISBN 978-3-8351-0018-3 (springer.com [abgerufen am 30. Dezember 2016]).
C. Hartsuijker, J. W. Welleman: Engineering Mechanics. Volume1: Equilibrium, ISBN 978-1-4020-4120-4, S. 64 (google.com).

Literatur

Alfred Böge: Vieweg Handbuch Maschinenbau. Grundlagen und Anwendungen der Maschinenbau-Technik. 18. Auflage. Vieweg-Verlag, Wiesbaden 2008, ISBN 978-3-8348-0110-4.
Rolf Mahnken: Lehrbuch der Technischen Mechanik. Grundlagen und Anwendungen. 2. Auflage. Band 1: Starrkörperstatik. Springer Vieweg, Berlin, Heidelberg 2016, ISBN 978-3-662-52784-9.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[egerer-1] H. Egerer: Ingenieur-Mechanik. Lehrbuch der technischen Mechanik in vorwiegend graphischer Behandlung. Band 1. Springer, Berlin, Heidelberg 1919, ISBN 978-3-662-32061-7, S. 124 (google.de [abgerufen am 3. Januar 2017]).

[2] M. B. Sayir, J. Dual, S. Kaufmann: Ingenieurmechanik 1. Grundlagen und Statik. Springer, 2008, ISBN 978-3-8351-0018-3 (springer.com [abgerufen am 30. Dezember 2016]).

[3] C. Hartsuijker, J. W. Welleman: Engineering Mechanics. Volume1: Equilibrium, ISBN 978-1-4020-4120-4, S. 64 (google.com).