Polplan

Der Polplan ist eine graphische Methode in der Statik (vorwiegend Baustatik), um ein System aus gelagerten und miteinander verbundenen Scheiben – wie im Bild – auf seine Stabilität hin zu untersuchen. Die Körper werden hier Scheiben genannt, weil dies bei ebenen Problemen naheliegt; sie können aber tatsächlich beliebig dreidimensional ausgeformt sein. Der Polplan trifft Aussagen darüber, ob das System statisch (fest und unverschieblich), kinematisch (verschieblich) oder teilkinematisch (in seinen Teilen oder Teile von ihm verschieblich) ist.

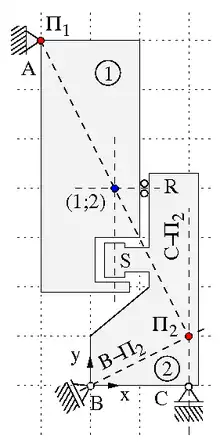
Zwei Scheiben (grau) werden von einem gelenkigen Festlager A und zwei einwertigen Lagern B und C gehalten. Die Scheiben sind über eine Schiebehülse S und ein Rollenlager R miteinander verbunden. Die Hauptpole sind rot und der Nebenpol blau markiert.

Zunächst wird das System auf statische Bestimmtheit geprüft. Ist es unterbestimmt, also ungenügend gelagert, werden weitere Lagerungen ergänzt, bis das System bestimmt oder unbestimmt gelagert ist. In diesem System wird mit den unten genannten Regeln der Polplan erstellt, wobei die Hauptpole und Nebenpole im System konstruiert werden. Der Hauptpol Π_i einer Scheibe i ist ihr Drehpunkt (rot im Bild) und jede Scheibe hat genau einen davon. Die Verbindungspunkte zweier Scheiben i und j definieren Nebenpole (i; j), um die sich die anliegenden Scheiben – sofern sie frei sind – drehen können.

Treten bei der Suche nach dem Hauptpol einer Scheibe Widersprüche auf, dann ist diese Scheibe unverschieblich und ihr Hauptpol kann nicht verortet werden. Treten bei der Suche nach dem Nebenpol (i; j) zweier Scheiben i und j Widersprüche auf, dann sind die Scheiben i und j fest miteinander verbunden und können als eine Scheibe betrachtet werden. Wenn über alle Haupt- und Nebenpole eines Systems eine definitive Aussage getroffen worden ist (ob die nun widerspruchsfrei gefunden wurden oder nicht), gilt der Plan als komplett. Wenn es nicht gelingt, alle Pole auf graphischem Weg zu bestimmen, können die Pole auch mit Polplangleichungen berechnet werden. Werden ein oder mehrere Hauptpole gefunden (im Bild sind es zwei), dann ist das System kinematisch oder teilkinematisch und als Tragkonstruktion ungeeignet. Nur wenn bei der Konstruktion des Polplans Widersprüche bei sämtlichen Hauptpolen auftreten, ist das System standfest.

Regeln für die Erstellung des Polplanes

Die Scheiben werden mit i=1, 2, 3, … durchnummeriert und jeder Scheibe wird ein Hauptpol Π_i zugewiesen. Die Verbindungen von Scheiben werden durch Nebenpole repräsentiert und für zwei miteinander verbundene Scheiben i und j mit (i; j) bezeichnet. Der Polplan wird mit den folgenden Regeln aufgestellt, die anhand des eingangs dargestellten Bildes erläutert werden sollen:

Eine fest eingespannte Scheibe ist unverschieblich und besitzt keinen Hauptpol. Alle Gelenkverbindungen zu dieser Scheibe werden zu entsprechenden Lagern und werden wie solche behandelt. Im Bild kann das gelenkige Festlager A (grau) als solche Scheibe angesehen werden.
Ein gelenkiges Festlager ist Hauptpol der anliegenden Scheiben. Im Bild befindet sich im Lager A der Hauptpol Π₁ der ersten Scheibe.
Der Hauptpol einer an ein verschiebliches Lager anliegenden Scheibe liegt auf der zur Bewegungsrichtung dieses Lagers senkrechten Geraden, die durch das Lager führt. Im Bild ist die Strecke vom Lager B zum Hauptpol Π₂ der zweiten Scheibe senkrecht zur Bewegungsrichtung des Lagers B.
Ein Momentengelenk bildet einen Nebenpol der anliegenden Scheiben. Wäre das Festlager A im Bild die dritte Scheibe, dann wäre ihre Verbindung mit der ersten Scheibe ein Momentengelenk und der Nebenpol (1; 3) wäre an der Stelle dieses Gelenkes.
Der Nebenpol zweier durch ein Normal- oder Querkraftgelenk verbundenen Scheiben liegt auf der zur Bewegungsrichtung des Lagers senkrechten Geraden, die durch das Lager führt. Im Bild ist die Strecke vom Nebenpol (1;2) zum Rollenlager R und zur Schiebehülse S senkrecht zu den Bewegungsrichtungen der Gelenke R bzw. S.
Die Hauptpole zweier Scheiben und ihr gemeinsamer Nebenpol liegen auf einer Geraden. Im Bild befindet sich der Nebenpol (1;2) auf der Verbindungsgeraden Π₁-Π₂ der Hauptpole der Scheiben eins und zwei (weshalb das System verschieblich ist).
Die Nebenpole dreier Scheiben liegen auf einer gemeinsamen Geraden.

Mögliche Ergebnisse

Werden alle Haupt- und Nebenpole gefunden, gilt das System als kinematisch (verschieblich) und ist somit nicht standfest. Falls im Polplan Widersprüche auftauchen (z. B.: ein Hauptpol ist bereits gefunden, aus Lager- bzw. Gelenkbedingungen geht jedoch eindeutig hervor, dass er zugleich auch an einem anderen Ort sein müsste), dann heißt das

bei einem Widerspruch im Hauptpol: die Scheibe ist fest (mit der Erdscheibe verbunden, quasi ein Teil der Erdscheibe) oder
bei einem Widerspruch im Nebenpol: die zwei durch Gelenke verbundenen Scheiben sind fest und starr aneinander (jedoch nicht notwendigerweise mit der Erdscheibe) festgemacht und wirken somit als eine Scheibe, auch wenn zwischen ihnen keine direkte materielle Verbindung besteht. Die neue Doppelscheibe besitzt nunmehr nur noch einen Hauptpol, der zu bestimmen ist.

Ein System mit Widersprüchen in allen Hauptpolen ist fest. Ein System, bei dem alle Hauptpole ohne Widerspruch gefunden werden können, ist verschieblich (kinematisch oder labil). Sind einige Scheiben fest, andere dagegen verschieblich, dann ist das System teilkinematisch.

Polplangleichungen

Die oben genannten Regeln zur Konstruktion des Polplanes definieren Punkte oder Geraden in der Ebene, in denen oder auf denen die Haupt- und Nebenpole liegen (müssen) und die mit Mitteln der analytischen Geometrie in Gleichungsform dargestellt werden können. Diese Gleichungen führen auf ein lineares Gleichungssystem, das vorteilhaft in Matrixform aufgeschrieben werden kann. Die lineare Algebra kennt Lösbarkeitskriterien, nach denen entschieden werden kann, ob das System keine, eine oder unendlich viele Lösungen besitzt.

Sollte keine Lösung existieren, dann heißt das, dass die Bestimmungsgleichungen für (mindestens) einen Punkt widersprüchlich sind.
1. Wenn der Punkt ein Nebenpol (i; j) ist, dann sind die in ihm anliegenden Scheiben i und j fest verbunden und können als eine Scheibe behandelt werden. Der Polplan und/oder die Gleichungen werden mit dieser neuen Doppelscheibe aufgestellt und erneut gelöst.
2. Wenn der Punkt ein Hauptpol Π_i ist, dann ist die Scheibe i unverschieblich. Ist die Scheibe die einzige verbleibende – unter Umständen nach Zusammenlegen von Scheiben gemäß der vorherigen Maßnahme –, dann ist der Polplan komplett und das System fest. Andernfalls – bei mehreren verbleibenden Scheiben – wird der Polplan und/oder die Gleichungen so, als wäre die Scheibe i fest eingespannt, neu aufgestellt und erneut gelöst.
Sollte genau eine Lösung existieren, dann heißt das, dass alle Scheiben im System verschieblich sind.
Unendlich viele Lösungen bedeuten, dass mindestens eine Scheibe verschieblich ist.

Beispiel

Für das im Bild oben dargestellte System aus zwei Scheiben soll die Erstellung des Polplans nachvollzogen werden. Zunächst ist die statische Bestimmtheit zu prüfen. In den Lagern wirken in A zwei, in B sowie C je eine und in den Gelenken R und S je zwei Reaktionen. Somit stehen 2+1+1+2+2=8 unbekannten Reaktionen 2*3=6 Gleichungen in Form von zwei Kräfte- und einer Momentengleichgewichtsbedingung je Scheibe gegenüber: Das System ist statisch unbestimmt. Nun soll mit dem Polplan geprüft werden, ob trotzdem Kinematiken auftreten.

Nach der zweiten Regel wird der Hauptpol der ersten Scheiben in das Lager A gelegt.
Nach der dritten Regel muss der Hauptpol der zweiten Scheibe auf der durch das Lager B führenden Senkrechten zur Bewegungsrichtung des Lagers B-Π₂ liegen.
Nach derselben Regel muss der Hauptpol der zweiten Scheibe auch auf der durch das Lager C führenden Senkrechten zur Bewegungsrichtung des Lagers C-Π₂ liegen. Der Schnittpunkt der Geraden B-Π₂ und C-Π₂ kennzeichnet den Hauptpol Π₂ der zweiten Scheibe.
Nach der fünften Regel liegt der Nebenpol (1;2), der die erste und zweite Scheibe verbindet, auf der durch das Rollenlager R führenden Senkrechten R-(1;2) zur Bewegungsrichtung des Lagers.
Nach derselben Regel liegt der Nebenpol (1;2) auch auf der durch die Schiebehülse S führenden Senkrechten S-(1;2) zur Bewegungsrichtung des Gelenkes. Im Schnittpunkt der beiden Senkrechten R-(1;2) und S-(1;2) liegt der Nebenpol (1;2).
Nach der sechsten Regel müssen die Hauptpole der ersten und zweiten Scheibe und der Nebenpol (1;2) auf einer Geraden liegen: Das ist der Fall.

Als Ergebnis kann festgestellt werden: Die beiden Hauptpole der Scheiben sind widerspruchslos dingfest zu machen, weswegen das betrachtete System kinematisch ist.

Mit Polplangleichungen ergibt sich ein identisches Ergebnis. Der Punkt A befinde sich an den Koordinaten (A_x, A_y) und die Punkte B, C, R und S entsprechend an den Koordinaten aus der Tabelle.

Punkt	A	B	C	R	S
x-Koordinate	−1	0	2	1	0,5
y-Koordinate	7	0	0	4	2,5

Die Steigung der Gleitrichtung des Lagers B sei −2, so dass die Senkrechte die Steigung 1/2 hat. Dann folgt:

Der Hauptpol der ersten Scheibe muss nach Regel zwei im Lager A liegen: ${\begin{pmatrix}\Pi _{1x}\\\Pi _{1y}\end{pmatrix}}={\begin{pmatrix}A_{x}\\A_{y}\end{pmatrix}}={\begin{pmatrix}-1\\7\end{pmatrix}}\,.$
Der Hauptpol der zweiten Scheibe muss nach Regel drei auf der Parallelen zur y-Achse durch den Punkt C liegen: Π_2x=C_x=2.
Des Weiteren muss der Hauptpol der zweiten Scheibe nach Regel drei auf der Senkrechten zur Bewegungsrichtung des Lagers B durch den Punkt B liegen: ${\frac {\Pi _{2y}}{\Pi _{2x}}}={\frac {\Pi _{2y}}{2}}={\frac {1}{2}}\;\rightarrow \quad \Pi _{2y}=1\;\rightarrow \quad {\begin{pmatrix}\Pi _{2x}\\\Pi _{2y}\end{pmatrix}}={\begin{pmatrix}2\\1\end{pmatrix}}\,.$
Nach der fünften Regel besitzt der Nebenpol (1;2) dieselbe x-Koordinate wie die Schiebehülse S, weil diese in x-Richtung verschieblich ist, und dieselbe y-Koordinate wie das Rollenlager R, weil dieses in y-Richtung verschieblich ist: $(1;2)={\begin{pmatrix}0,5\\4\end{pmatrix}}\,.$
Bleibt zu prüfen, ob der Nebenpol (1;2) gemäß der sechsten Regel auf der Geraden zwischen den beiden Hauptpolen (Π₁ Π₂) liegt. Das ist der Fall, denn der Nebenpol liegt genau in der Mitte zwischen beiden Hauptpolen: : $(1;2)={\begin{pmatrix}0,5\\4\end{pmatrix}}={\frac {1}{2}}\left[{\begin{pmatrix}-1\\7\end{pmatrix}}+{\begin{pmatrix}2\\1\end{pmatrix}}\right]$

Damit sind alle Hauptpole und Nebenpole ermittelt und mithin das System in allen Teilen verschieblich.

Freikörperbilder der Scheiben aus dem eingangs dargestellten System aus zwei Scheiben.

Abhilfe könnte eine der folgenden Maßnahmen schaffen:

Das Lager B oder C verschieben, so dass Π₂ nicht mehr auf der Geraden Π₁-(1;2) liegt.
Die Gleitrichtung des Lagers B ändern, so dass Π₂ nicht mehr auf der Geraden Π₁-(1;2) liegt.
Die Gelenke R oder S verschieben oder verdrehen, so dass der Nebenpol (1;2) nicht mehr auf der Verbindungsgeraden der beiden Hauptpole liegt.

Eine dieser Maßnahmen würde bewirken, dass der Nebenpol (1; 2) nicht mehr widerspruchsfrei festgelegt werden könnte, weswegen beide Scheiben nunmehr fest miteinander verbunden und wie eine Scheibe zu behandeln wären. Der Hauptpol Π dieser neuen Doppelscheibe müsste nach der zweiten Regel im Lager A und nach der dritten Regel im Schnittpunkt der Geraden Π-B und Π-C gleichzeitig liegen, was unmöglich ist: Das modifizierte System wäre fest.

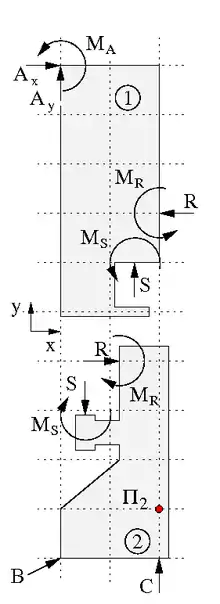
Die Berechnung der Lagerreaktionen anhand der Freikörperbilder der beiden Scheiben in nebenstehender Abbildung bestätigt die Verschieblichkeit. Als Ursache für die Lagerreaktionen wird im Lager A ein von außen angreifendes Moment M_A angenommen. In gleicher Weise werden die Reaktionsmomente M_R,S in den Gelenken R und S bezeichnet. Das Momentengleichgewicht in den beiden Hauptpolen liefert zwei Gleichungen für die beiden Gelenkreaktionen R und S in den gleichnamigen Gelenken und die dortigen Reaktionsmomente:

{\begin{array}{rcl}\sum M_{i\Pi _{2}}&=&-3R+1,5S-M_{R}-M_{S}=0\\\sum M_{iA}&=&M_{A}-3R+1,5S+M_{R}+M_{S}=M_{A}+2M_{R}+2M_{S}=0\,.\end{array}}

Wenn die Gelenke keine Momente aufnehmen sollen (oder können), dann muss für M_A=0 gesorgt werden: Das System erweist sich als anfällig für Drehungen.

Literatur

Rolf Mahnken: Lehrbuch der Technischen Mechanik. Grundlagen und Anwendungen. 2. Auflage. Band 1: Starrkörperstatik. Springer Vieweg, Berlin, Heidelberg 2016, ISBN 978-3-662-52784-9.
Christian Spura: Technische Mechanik 1. Stereostatik. 1. Auflage. Springer Vieweg, Wiesbaden 2016, ISBN 978-3-658-14984-0.

Siehe auch

Momentanpol

Weblinks

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.