Seileckverfahren
Das auf Pierre de Varignon zurückgehende Seileckverfahren[1] ist ein zeichnerisches Verfahren in der Statik zur Bestimmung der resultierenden Kraft (Resultierende), aus der man dann, z. B. mit Hilfe des Culmann-Verfahrens, die Auflagerreaktionen ermitteln kann.
Liegen mehrere Kräfte in einer Ebene, die nicht an einem gemeinsamen Punkt angreifen, kann die Lage der Resultierenden mit diesem Verfahren ermittelt werden: Es wird eine Figur – das sogenannte Poleck[2] – gezeichnet, worin die Einzelkräfte als Kräftepfeile addiert werden, um Größe und Richtung der Resultierenden zu bestimmen und die dann durch Polstrahlen mit einem Punkt, der Pol verbunden werden. Die Polstrahlen werden dann als sogenannte Seilstrahlen in den Lageplan übertragen, wo sie das Seileck bilden und die Ermittlung der Wirkungslinie der Resultierenden ermöglichen.[3] Der Begriff Seileck wird im weiteren Sinne auch für das Poleck verwendet.
Verfahren
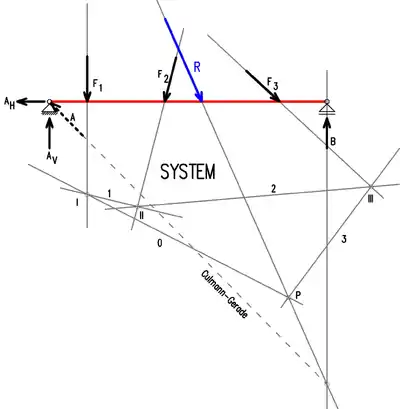
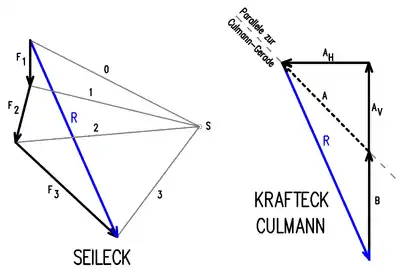
Im Beispiel ist ein Balken auf zwei Stützen A und B gegeben, an dem die Kräfte F1, F2 und F3 entsprechend der Skizze angreifen. Zunächst werden die Kräfte entsprechend der unteren Skizze maßstäblich als Kräftepfeile gezeichnet und geometrisch addiert. Dabei werden die Kräfte F1, F2 und F3 auf ihren Wirkungslinien fortlaufend aneinandergereiht so dargestellt, dass auf eine Pfeilspitze der Pfeilanfang der nächsten Kraft folgt. Verbindet man den Pfeilbeginn von Kraft F1 mit der Pfeilspitze von Kraft F3, so erhält man die resultierende Kraft R nach Größe und Richtung. Danach zieht man von einem beliebig gewählten Punkt S sogenannte Polstrahlen (Verbindungslinien) zu den Enden der einzelnen Kräftepfeile und nummeriert sie fortlaufend. Die so entstandenen Dreiecke stellen Kraftecke dar, deren Polstrahlen sich mit den zugehörigen Kräften in den Punkten I,II, III und P der oberen Skizze schneiden.
Mit der Konstruktion des Seilecks entsprechend der oberen Skizze ergibt sich die Lage der resultierenden Kraft R. Man beginnt mit der Wirkungslinie der Kraft F1 und bringt diese mit den zugehörigen Polstrahlen aus dem Krafteck, das sind 0 und 1, im Punkt I zum Schnitt. Mit den Kräften F2 und F3 verfährt man genauso. Im Schnittpunkt P der Polstrahlen 0 und 3 liegt die Wirkungslinie der resultierenden Kraft R, deren Angriffspunkt am Balken durch verschieben des Kräftepfeils bestimmt ist. Die gleichen Wirkungslinien der Kräfte und von den Polstrahlen in den verschiedenen Skizzen müssen natürlich immer parallel sein.
Die Auflagerreaktionen werden hier mit Hilfe des Culmann-Verfahrens ermittelt:
Man bringt die Wirkungslinie der Resultierenden R mit einer Auflagerwirkungslinie (hier B) zum Schnitt. Diesen Schnittpunkt verbindet man mit dem Schnittpunkt der anderen beiden Auflagerwirkungslinien (hier AV und AH). Diese Verbindungslinie ist die sogenannte Culmanngerade.
Nun bildet man ein Krafteck aus der Resultierenden R mit den Wirkungslinien aus den gesuchten Auflagerreaktionen A (AV und AH) und B. Man kann dieses Krafteck auch im Seileck darstellen, zur besseren Übersichtlichkeit wurde hier ein getrenntes Krafteck gezeichnet.
Siehe auch
Einzelnachweise
- Karl-Eugen Kurrer: The History of the Theory of Structures. Searching for Equilibrium. Ernst & Sohn, Berlin, ISBN 978-3-433-03229-9, S. 453
- Poleck. Baulexikon, Beuth Verlag
- Seileck. Baulexikon, Beuth Verlag