Koppelgetriebe

Die Koppelgetriebe sind eine der sechs grundlegenden Arten von Getrieben. Unter allen Getriebearten sind sie diejenigen, die die größte Vielfalt an Strukturen und Eigenschaften aufweisen.[1] Sie werden sowohl als Übertragungsgetriebe als auch als Führungsgetriebe verwendet.[2] Zusammen mit den Kurvengetrieben bilden sie die Gruppe der ungleichmäßig übersetzenden Übertragungsgetriebe.[3]

Koppelgetriebe „sind Getriebe mit mindestens vier Festkörper-Gliedern, die durch Gleitgelenke verbunden sind. Alle Koppelgetriebe enthalten mindestens eine feste Koppel, d.h.ein Getriebeglied, das im einfachsten Fall die beiden im Gestell gelagerten Glieder verbindet.“[2] Als viergliedrige und viergelenkige Koppelgetriebe werden sie auch als Viergelenkgetriebe[4] oder als bewegliche Vierecke, d. h. Gelenkvierecke[5] bezeichnet.

Kurbelschwinge mit Bahnkurve eines Punkts der Koppel (Koppelkurve). Das blaue Dreieck stellt die Koppel dar. Die eingezeichnete Verbindung zwischen den beiden Fixpunkten verdeutlicht, dass die Basis ("das Gestell") als Glied des Koppelgetriebes anzusehen ist.

Sofern Glieder des Koppelgetriebes an "Fixpunkten" gelagert sind, so wird die gemeinsame Basis der Fixpunkte als "Gestell" bezeichnet. Das Gestell ist gleichbedeutend mit einem der Glieder des Koppelgetriebes. Die vier Gelenke der einfachsten Grundform des Koppelgetriebes haben jeweils nur einen Freiheitsgrad. Ein Drehschubgelenk würde als Kombination eines Dreh- und eines Schubgelenks betrachtet, die jeweils einen Freiheitsgrad besitzen. Die Verbindung zwischen beiden Gelenken kann dann als Koppel angesehen werden (auch wenn diese Verbindung je nach Bauform des Gelenks nicht als separates Glied erkennbar ist).

Nach der gegenseitigen Lage der Drehachsen der Gelenke werden sie unterteilt in

ebene Getriebe mit parallelen Drehachsen der Gelenke und
räumliche Getriebe mit sich kreuzenden Drehachsen der Gelenke.[6]

Die Gelenke ebener Getriebe können alle den Freiheitsgrad f=1 haben. In räumlichen Getriebe sind immer einige Gelenke mit Freiheitsgrad f>1 enthalten,[7] wie etwa Kugelgelenke (f=3).

Zwei Grundformen der viergliedrigen ebenen Koppelgetriebe sind:

die Kurbelschwinge mit einem umlaufenden (Kurbel-)Glied und
die Schubkurbel mit drei Drehgelenken und einem Schubgelenk.

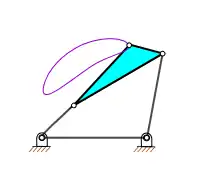
Zwischen den beiden am Gestell gelagerten Gliedern befindet sich das Koppel genannte Übertragungsglied, was den Namen Koppelgetriebe erklärt. Mehr-gliedrige Koppelgetriebe besitzen mehrere Zwischenglieder, die alle als Koppel bezeichnet werden.[8] Bei Übertragungsgetrieben fungiert die Koppel entsprechend den beiden anderen beweglichen Gliedern als Übertragungsglied zwischen An- und Abtrieb. Bei Führungsgetrieben ist sie ein geführtes oder ein führendes (welches weitere, mit dem Koppelgetriebe verbundene Glieder führt) Getriebeglied.[9] Dabei wird die Variationsbreite möglicher Bahnformen von Punkten der Koppel oder mit ihr verbundener Punkte ausgenutzt (s. a. nebenstehende Abbildung).[10] Bei ebenen Getrieben handelt es sich dabei um algebraische Kurven 6. Ordnung,[11] die Koppelkurven genannt werden.

Bezeichnungen der Getriebeglieder [12][13][14]

Koppel

„Mit dem Gestell nicht direkt verbundene Getriebeglieder heißen grundsätzlich Koppel.“[9]

Am Gestell angeschlossene Getriebeglieder

„Am Gestell angeschlossene Getriebeglieder werden entsprechend ihrer Beweglichkeit gegenüber dem Gestell bezeichnet“:[9]

Es existieren die folgenden Bezeichnungen:[15]

Kurbel

Die Kurbel ist ein am Gestell und an der Koppel drehbar angeschlossenes Getriebeglied. Sie läuft am Gestell um.

Schwinge

Die Schwinge ist ein am Gestell und an der Koppel drehbar angeschlossenes Getriebeglied, das am Gestell lediglich schwingt, aber keinen vollen Umlauf vollzieht.
Bei der Automobil-Pendel- oder Schwingachse und der Motorrad-Hinterradschwinge wird der Begriff Schwinge auch verwendet, ohne dass diese Schwinge Teil eines Koppelgetriebes ist. Der Radträger (Achsschenkel) ist jeweils fest am schwingenden Ende des Schwingarms befestigt.

Schleife

Die Schleife ist ein am Gestell drehbar und an der Koppel schiebbar angeschlossenes Getriebeglied. Am Gestell kann sie umlaufen (Kurbelschleife) oder nur schwingen.

Schieber

Der Schieber ist ein im Gestell schiebbar gelagertes Getriebeglied. Nachbarglieder sind an ihm über ein Drehgelenk angeschlossen.

Kreuzschieber

Der Kreuzschieber ist ein am Gestell und an der Koppel schiebbar angeschlossenes Getriebeglied. Am Gestell ist er nur schiebbar.

Ebene, sphärische und räumliche Koppelgetriebe

Kardangelenk mit eingezeichneten Drehachsen, die sich alle in einem Punkt schneiden

Ebene und sphärische Koppelgetriebe

Die Achsen sphärischer Getriebe treffen sich in einem Punkt. Ein Beispiel für sphärische Getriebe ist die Kombination aus zwei auf dem Gestell drehbar gelagerten Wellen und einem sie verbindenden Kardangelenk (siehe nebenstehende Abbildung). Die Achsen der Wellen und der beiden Drehgelenke des Kardangelenks kreuzen sich im Punkt (dem das Kardangelenk auch seinen Namen Kreuzgelenk verdankt).

Die ebenen Getriebe sind ein Sonderfall sphärischer Getriebe, bei dem die Achsen der Lager parallel zueinander liegen. Bezüglich der auftretenden Kräfte, der Steifheit der Getriebeglieder und anderer physikalischer Faktoren sind Konstruktion und Dimensionierung sphärischer Getriebe aufwändiger.

Ein räumlicher Kurbeltrieb mit einem Kugelgelenk zwischen Kurbel und Koppelglied und einem Drehgelenk zwischen Koppel und Schubstange. Die grüne Schubstange ist in einem Drehschubgelenk gelagert. Durch die drei Bewegungsfreiheiten des Kugelgelenks kann die Ausrichtung der Schubstange innerhalb eines weiten Bereiches räumlich beliebig variiert werden. Wenn die rotierende rote Antriebswelle zur grünen Schubstange einen anderen Winkel als 90 Grad einnimmt, so wird zusätzlich zur erzeugten Schubbewegung auch die Drehbewegung der Antriebswelle übertragen (vergleichbar mit dem Kardangelenk).

Räumliche Koppelgetriebe

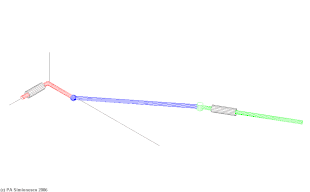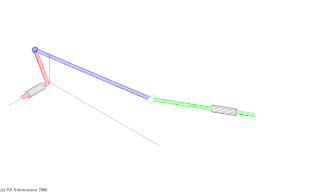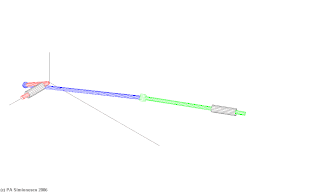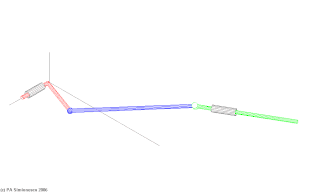
Bei räumlichen Koppelgetrieben (Raumgetrieben) liegen die Drehachsen der Gelenke beliebig im Raum. Neben einfachen Dreh- und Schubgelenken (f=1) kommen auch Gelenke mit f>1 vor (f=2: Drehschub- und f=3: Kugelgelenke). Die theoretische und praktische Beherrschung von räumlichen Koppelgetrieben ist sehr viel aufwändiger als die der ebenen und sphärischen Getriebe. Die folgenden Darstellungen beziehen sich mit Ausnahme eines kurzen Abschnitts im nächsten Kapitel ausschließlich auf ebene Koppelgetriebe.

Wichtiges Anwendungsfeld räumlicher Koppelgetriebe sind moderne Radaufhängungen von Fahrzeugen.

Zahl der Getriebeglieder

Im Minimum hat ein Koppelgetriebe vier Glieder. Mit nur drei Gliedern wäre es nicht beweglich, sofern nicht eines der Gelenke zwei Bewegungsfreiheiten hat, wie z. B. ein in einem Schlitz verschieb- und drehbarer Stift (f=2). Die Bewegungsfreiheit oder der Laufgrad eines Getriebes als Gesamtheit soll i. d. R. F=1 sein, damit alle seine Glieder dem Antriebsglied zwangläufig folgen.

Wenn mehr als ein Glied antreibend sein soll (F>1), werden entsprechend der Grüblerschen Gleichung im Minimum fünf Glieder benötigt (5-gliedrig bei 2 Antrieben; F=2[16]):

{\begin{aligned}F&=\ 3\cdot (n-1-g)+c\end{aligned}}

Gleichung für ebene Getriebe, die keine Gelenke mit mehr als einer Bewegungsfreiheit enthalten.

n = Gliederzahl

g = Gelenkzahl

c = Gelenkzahl mit f=1

Zweck eines mehrfachen Antriebs ist, die Bewegungen der antreibenden Glieder in besonderer Übertragungsfunktion (Abtriebsparameter ψ = ψ(φ₁,φ₂,.. ) ; φ_i = Antriebsparameter[17]) zu summieren.

Im Unterschied zu viergliedrigen Koppelgetrieben existiert bei Koppelgetrieben mit mehr als vier Gliedern keine umfassende Ordnung (Klassifizierung).[9]

Vier Glieder

F = 2 ≠ 3 (4 − 1 − 4) + 4 >> F=2 ist nicht möglich !
(F = 1 = 3 (4 − 1 − 4) + 4 >> F=1 ist aber möglich.)

Fünf Glieder

F = 2 = 3 (5 − 1 − 5) + 5 >> F=2 ist möglich !

Sechs und mehr Glieder

Die Grüblersche Gleichung zeigt, dass Koppelgetriebe mit dem gewünschten Laufgrad F=1, also mit nur einem angetriebenen Glied, immer aus einer geraden Zahl von Gliedern bestehen.

Sechsgliedrige Drehgelenkketten unterscheiden sich in der gegenseitigen Lage der beiden Dreigelenkglieder und heißen Stephenson'sche und Watt'sche Kette.[18]

Parallelkurbelgetriebe an der Dampflokomotive Saxonia.
Eine zweite Koppelstange befindet sich an den gegenüberliegenden Rädern.

Sonderabmessungen: „übergeschlossene Getriebe“

In der Praxis sind auch funktionierende Getriebe anzutreffen, bei denen die Zwanglaufgleichungen nicht erfüllt sind. Ein Beispiel ist das zweifache Parallelkurbelgetriebe zur Übertragung einer Drehbewegung von einer Welle auf eine zweite,[19] wie in an einer Dampflokomotive. Die zweite Koppelstange steht gegen die erste um 90° versetzt, da dies zum Vermeiden des Umschlagen eines Radpaares erforderlich ist (sollte die Lokomotive einmal nicht auf den Gleisen stehen). Daher wird F=0 :

F=\ 3\cdot (n-1-g)+c

F = 3 (5−1−6) + 6 = 0
Dieser Widerspruch ergibt sich aus Sonderabmessungen: Die beiden Koppelstangen und die vier Kurbeln sind je untereinander gleich lang. Die Gleichheiten müssen bei der Fertigung mit hoher Genauigkeit gewährleistet werden. Bei Ungenauigkeiten klemmt das Getriebe oder ist nur soweit beweglich, wie es das Gelenkspiel zulässt.[20][21]

Kreuzgelenk: rechte Winkel zwischen benachbarten Drehachsen

Viergliedriges Raumgetriebe

Ein zwangläufiges (F=1) viergelenkiges Raumgetriebe benötigt gemäß Grüblerscher Gleichung

F=\ 6\cdot (n-1-g)+\sum _{i=1}^{g}b_{i}

in der Summe sieben Gelenkbewegungsfreiheiten, und kann somit höchstens zwei einfache Gelenke haben.[22]
Kontrollrechnung: Mit F=1 und n=g=4 (4 Glieder und 4 Gelenke) ist die Summe der Gelenkbewegungsfreiheiten $\sum _{i=1}^{g}b_{i}=7.$

Bekanntes Beispiel eines Raumgetriebes ist das Kreuzgelenk (Kardangelenk). Infolge von Sonderabmessungen (rechte Winkel zwischen benachbarten Gelenken, die mit hoher Genauigkeit gefertigt werden müssen) funktioniert es als 4-gliedriges Raumgetriebe mit nur 4 einfachen (f=1) Gelenken.
Es repräsentiert nicht den allgemeinen Fall der Raumgetriebes.

Übertragung

Kennzeichen der Koppelgetriebe ist, dass sie eine (gleichmäßige) Drehbewegung in eine periodisch veränderliche Bewegung umformen. Das Abtriebsglied dreht um eine feste Achse hin und her (oder läuft um), geht auf einer geraden Bahn hin und her oder wird auf einer Bahn höherer Ordnung (Koppelkurve) geführt.[23]

Übertragungswinkel

Der Übertragungswinkel (Winkel am Gelenk zwischen den beiden als Geraden zu denkenden Gliedern) ist „ein Kriterium für die Güte der Kraft- und Bewegungsübertragung“. Er sollte innerhalb von 90°±50° bleiben. Bei den Werten 0° und 180° ist eine Übertragung „nicht möglich, das Übertragungsgetriebe ist nicht lauffähig.“[24]

Stetige Änderung der Übertragung

In den meisten Anwendungen von Koppelgetrieben ändert sich die Übertragung stetig.

Unstetige Übertragung

Getriebe, bei denen ein Abtriebsglied zeitweise in Ruhelage ist bzw. eine Schrittbewegung ausführt, heißen Schrittgetriebe,[25] Schaltwerke[26] oder Rastgetriebe. Mit Koppelgetrieben ist eine längere und exakte Ruhelage schwieriger als mit Kurvengetrieben zu erreichen und erfordert i. d. R. mehr als 6 Getriebeglieder.[27]

Die Ordnung der viergliedrigen Koppelgetriebe

„Für eine wissenschaftlich begründete Arbeit ... ist bei der außerordentlich großen Vielfalt der Koppelgetriebe eine eindeutige Ordnung dieser Getriebeart ... unerlässlich.“[28]

Ordnung der viergliedrigen Koppelgetriebe nach drei primären Merkmalen:[9]

Strukturmerkmale, d. h. Anzahl der Dreh- und Schubgelenke und deren gegenseitige Anordnung,
Längenverhältnisse der Getriebeglieder und den daraus resultierenden Übertragungsfunktionen und Koppelkurven und
Verteilung der Gliederfunktionen, d. h. Gestell, Antriebs- oder Abtriebsglied.

Innerhalb der Strukturmerkmale wird unterschieden in:[29]

Koppelgetriebe mit vier Drehgelenken (Viergelenkkette),
Koppelgetriebe mit drei Dreh- und einem Schubgelenk (Schubkurbelkette),
Koppelgetriebe mit je zwei benachbarten Dreh- und Schubgelenken (Kreuzschubkurbelkette),
Koppelgetriebe mit je zwei gegenüberliegenden Dreh- und Schubgelenken (Schubschleifenkette).

Getriebe der Viergelenkkette

Getriebe der Viergelenkkette
Doppelkurbel - Kurbelschwinge - Doppelschwinge - Parallelkurbel ( ein durchschlagendes Getriebe)

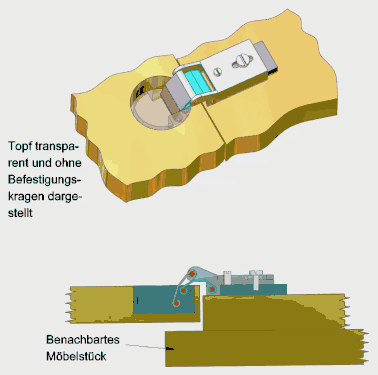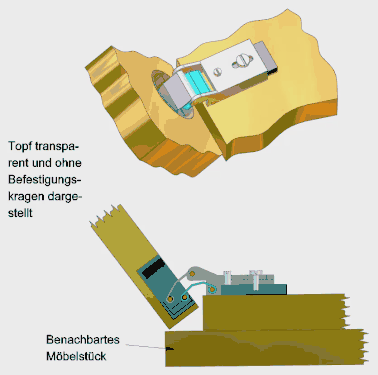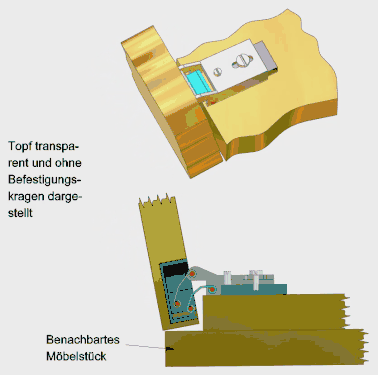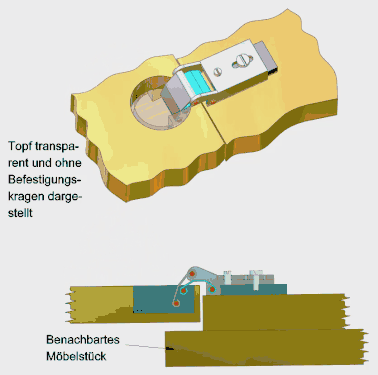
Beispiel aus dem Möbelbau: Topfscharnier (animiert)

Je nachdem, ob das kürzeste Glied die Kurbel, die Koppel oder das Gestell ist, handelt es sich um:[30][31]

eine Kurbelschwinge,
eine Doppelschwinge[32] (Totalschwinge[29]) oder
eine Doppelkurbel.[33]

Die Längen s, l, p und q der Glieder bestimmen, ob ein Glied gegenüber seinen beiden benachbarten Gliedern umlauffähig ist. Die Längenbedingung dafür lautet nach Grashof:
s + l < p + q .

Bei Gleichheit liegen durchschlagende Getriebe vor. Das kürzeste Glied ist gerade noch umlauffähig, aber es gibt Lagen, in denen sich die vier Drehgelenke in einer Geraden befinden. In diesen fehlt der Zwanglauf: Das Getriebe kann durchschlagen, aber auch in die entgegengesetzte Bewegung zurückschlagen (was durch konstruktive Zusatzmaßnahmen verhindert werden kann).

Bei umgekehrter Bedingung
l + s > p + q .
sind alle Glieder relativ zueinander nur schwingfähig wie bei der Doppelschwinge (oder Totalschwinge).

Getriebe der Schubkurbelkette

zentrische Schubkurbel

ein Getriebe der Kreuzschleifenkette
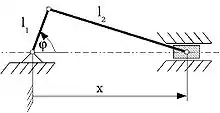
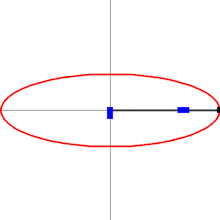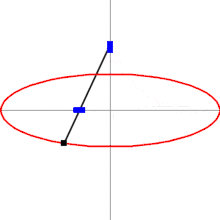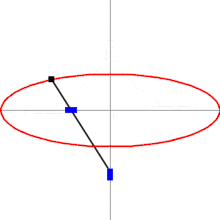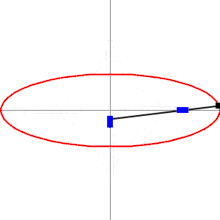
rechtwinkliger Doppelschieber (Ellipsenzirkel)

[34]

Es gibt nur die beiden Glieder mit den Längen l₁ und l₂ (s. nebenstehende Abbildung; die Glieder 3 und 4 – der Schubstein und seine Bahn – sind im kinematischen Sinn unendlich lang).

Die Schubkurbelkette ist zentrisch, wenn die Schubachse durch ein Drehgelenk an der Schubstange oder am Schubstein geht. Je nachdem, welches Glied Gestell ist, wird unterschieden in:[35]

Die Schubbahn ist Gestell – (zentrische) Schubkurbel.
Glied l₁ (< l₂) oder Glied l₂ (< l₁) ist Gestell – umlaufende Kurbelschleife (wenn l₁ = l₂, dann gleichschenklig durchschlagend).
Glied l₁ (> l₂) oder Glied l₂ (> l₁) ist Gestell – schwingende Kurbelschleife.[36] (wenn l₁ = l₂, dann gleichschenklig durchschlagend).
Der Schubstein ist Gestell – Schubschwinge, mit umlaufender Koppel l₁ (< l₂).

Ist die Schubkurbelkette exzentrisch (Schubachse geht nicht durch das Drehgelenk; der Abstand von ihm ist die Exzentrizität e), so gelten Bedingungen für die Umlauffähigkeit:
umlauffähig, wenn e < |l₁ - l₂| ,
durchschlagend, wenn e = |l₁ - l₂| ,
nicht umlauffähig, wenn e > |l₁ - l₂| (obige Aufzählung wird ergänzt durch eine nichtumlaufende Schubschwinge und eine Schwingschleife)[37] .

Getriebe der Kreuzschleifenkette

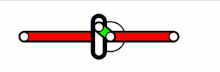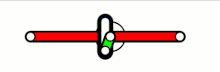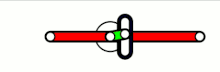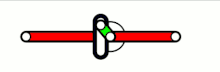
ein Getriebe der Kreuzschleifenkette[38]
rechtwinklige Kreuzschubkurbel

Zur Auslegung von Kreuzschubkurbelketten-Getrieben genügen die Angaben Kreuzungswinkel der Schubrichtungen (am günstigsten sind 90°) und Länge des Glieds zwischen den beiden Drehgelenken. Bei der Kreuzschubkurbel (Abbildung links) ist die Hin- und Herbewegung des Schubglieds im Gestell exakt sinusförmig. Bei der gewöhnlichen Schubkurbel kann die Sinusform nur mit langer Schubstange angenähert werden.

Relativ zum Schubbahnkreuz sind die Bahnen der Punkte des Gliedes mit Drehgelenken Ellipsen, was die Verwendung des Getriebes als Ellipsenzirkel ermöglicht (Doppelschieber, Abbildung rechts).[39]

Beispiel eines Getriebes der Kreuzschleifenkette ist auch die Oldham-Kupplung.

Getriebe der Schubschleifenkette

Für Schubschleifengetriebe[40] (zwei gegenüberliegende Drehgelenke sind durch Schubgelenke ersetzt) ist charakteristisch, dass keines der Glieder umlauffähig ist.[39] Anwendung in der Feinwerktechnik im Zusammenhang mit Schalt- und Stellmechanismen.[41]

Räderkoppelgetriebe

Kombinierte Getriebe entstehen durch Hintereinander- oder Parallelschaltung von Getrieben verschiedener Getriebearten, um die Vorzüge einzelner Getriebearten zu vereinigen.[42]

Räderkoppelgetriebe sind Kombinationen von Koppelgetrieben mit Zahnrädern. Sie werden vorwiegend zur Erzeugung ungleich mäßig umlaufender oder schwingender Drehbewegungen verwendet.[43]

Dreiräder-Koppelgetriebe

Von den Räderkoppelgetrieben wird am häufigsten das mit einer Kurbelschwinge kombinierte Dreiräder-(Zahnräder)-Koppelgetriebe eingesetzt. Mit ihm werden umlaufende, stark ungleichmäßige Drehbewegungen, auch mit Rast oder Pilgerschritt (Teilrückdrehung) für Anwendungsfälle in Textil-, Verpackungs- und anderen Maschinen erzeugt.[44]

Ein Beispiel ist der Antrieb einer Papiertrommel in einer Papierwendeeinrichtung bei Druckmaschinen. Hierbei führt die sich mit hoher Drehzahl drehende Trommel nach jeder Umdrehung eine momentane Rast aus, so dass der Greifer, der das bedruckte Blatt wendet, Gelegenheit hat, exakt und sicher zuzugreifen.

Watt’sches Planetengetriebe youtube.com,
Hinter den beiden Zahnrädern befindet sich (kaum sichtbar) eine Kurbel, die hier allerdings keine Kräfte übertragen muss, sondern zuvorderst dazu dient, die Zahnräder auf einem gleichmäßigen Abstand zu halten.

Watt’sches Planetengetriebe

James Watt umging bei der Umwandlung der Hub- in Drehbewegungen einer Kolben-Dampfmaschine mit einem Zusatz an der Schubkurbel das damals lizenzpflichtige Patent auf letztere. Er befestigte am rotierenden Ende der Koppel ein Zahnrad (Planetenrad), das mit einem koaxial mit der Kurbel gelagerten Zahnrad kämmte. Abtrieb war nicht die Kurbel, sondern das im Vergleich zu ihr doppelt schnell drehende Zahnrad.

Analyse

Die Getriebeanalyse ist eine allgemeine, bei allen Getrieben ähnlich zu lösende Aufgabe. Bei Koppelgetrieben ist sie wegen deren ungleichmäßigen Bewegungen umfassender und aufwändiger als z. B. bei konstant übersetzenden Rädergetrieben.

Zu ermitteln ist das kinematische und kinetische Verhalten der Teile eines vorgegebenen Getriebes.[45] Das vorgegebene Getriebe kann auch ein näherungsweises Ergebnis der Getriebesynthese sein, das zur Vorbereitung des nächsten iterativen Entwicklungsschritts zu analysieren ist.

Getriebekinematik: Bewegung der Getriebeteile ohne Beachtung ihrer Massen und Bewegungsursachen. Die Bewegung der Getriebeteile bestimmt im Wesentlichen die Funktion des Getriebes. Ihre Kenntnis ist die Grundlage der
Getriebekinetik (-dynamik): Einbezug der Massen, Bewegungsursachen (u. a. das Antriebsmoment) und Kräfte, die maßgebend für die Beanspruchung der Teile sind. Mit den Kräften kann ihre Festigkeit nachgewiesen werden.

Physikalische Grundgrößen der Getriebeanalyse sind Zeit, Weg und Masse. Daraus abgeleitete Größen sind Geschwindigkeit, Beschleunigung und Trägheitskraft. Wird die Untersuchung in einem bestimmten Moment an einem bestimmten Punkt eines Getriebegliedes vorgenommen, so liegt eine quasi-statische Aufgabe (kineostatische Analyse[46]) vor.

Die Getriebeanalyse wird zeichnerisch und rechnerisch durchgeführt, wobei die zeichnerischen Verfahren den Vorteil der Anschaulichkeit und der schnellen Durchführbarkeit haben.[45] Bei Anwendung von CAD sind ermittelte geometrische Größen bereits genau genug, sie müssen nicht mehr nachträglichem geometrischem Rechnen unterworfen werden. Bei der rechnerischen kinematischen Analyse steht die Ermittlung der Übertragungsfunktion (Bewegung des getriebenen in Abhängigkeit vom treibenden Glied) meist an erster Stelle.[47]

Besondere Fragestellungen bei der Analyse von Koppelgetrieben sind die nach den

Koppelkurven und den
Momentanpolen

Synthese

Ein Getriebe soll entweder eine vorgegebene Übertragungsfunktion oder eine vorgegebene Führungsbahn ermöglichen.[48] Zunächst wird mithilfe der Strukturanalyse ein geeigneter Getriebetyp für die gestellte Aufgabe ermittelt. Mögliche Übertragungsfunktionen viergliedriger Koppelgetriebe ergeben sich aus der Getriebesystematik (siehe Abschnitt Die Ordnung der viergliedrigen Koppelgetriebe). Sie sind nicht immer hinreichend, z. B. ist für eine Bewegung mit Rast unbedingt ein sechsgliedriges Koppelgetriebe erforderlich. Deren grundsätzliches Verhalten ist im Unterschied zu dem der viergliedrigen Koppelgetriebe weniger gut bekannt. Es gibt aber zahlreiche Sammlungen von Beispielen (Getriebeatlanten) erprobter höhergliedriges Koppelgetriebe, auf die sich der Konstrukteur stützen kann.

In der Regel wird die Synthese mithilfe einer iterative Analyse durchgeführt. Wie bei dieser kann zeichnerisch und rechnerisch vorgegangen werden. Das anschauliche zeichnerische Vorgehen lässt sich anschließend – wenn erforderlich – rechnerisch nachvollziehen. Häufig kann das vorgegebene Ziel nur näherungsweise erreicht werden. Die zu realisierende Übertragungsfunktion wird dann entweder

nur in ausgewählten Punkten erreicht, oder
es genügt, wenn die realisierte Funktion innerhalb eines bestimmten Toleranzbandes liegt.

Exakt und explizit kann die Übertragungsfunktion eines viergliedrigen Koppelgetriebes nur für fünf Funktionspunkte bestimmt werden.

Siehe auch

Dynamische Geometrie mit hilfreichen Programmen für die Synthese.
Mehrkörpersystem
Übertragungswinkel
Mehrgelenkscharnier

Literatur

Johannes Volmer (Hrsg.): Getriebetechnik – Koppelgetriebe Verlag Technik, 1979.
Johannes Volmer (Hrsg.): Getriebetechnik – Grundlagen Verlag Technik, 1995, ISBN 3-341-01137-4.

Weblinks

Commons: Koppelgetriebe – Sammlung von Bildern, Videos und Audiodateien

Ebene Koppelgetriebe nach Lichtenheld (MS Word; 135 kB)
Digitale Mechanismen- und Getriebebibliothek (DMG-Lib)
Getriebeanalyseprogramm KINTOP (Getriebetechnik, RWTH Aachen, University)
Übersicht der Getriebeanalyseprogramme (Getriebetechnik, RWTH Aachen, University)

Einzelnachweise

Johannes Volmer (Hrsg.): Getriebetechnik - Koppelgetriebe Verlag Technik, 1979, S. 24
Volmer: Koppelgetriebe, S. 13
Johannes Volmer (Hrsg.): Getriebetechnik - Grundlagen Verlag Technik, 1995, ISBN 3-341-01137-4, S. 27
Volmer, Koppelgetriebe, Seite 25. Am Anfang (19. Jahrh.) wurde des Viergelenkgetriebe noch Dreistabgetriebe genannt.
Kerle u.A.: Getriebetechnik. Springer-Verlag, 2015, S. 10 (Volltext in der Google-Buchsuche).
Volmer: Grundlagen S. 240
Volmer: Grundlagen S. 241
vgl. Volmer: Grundlagen, S. 184–185.
Volmer: Grundlagen, S. 184–185
Dankert/ Dankert: Technische Mechanik. Beispiele für Koppelgetriebe inkl. animierter Darstellung von Koppelkurven tm-aktuell.de
Volmer: Grundlagen, S. 195.
Johannes Volmer: Getriebetechnik - Lehrbuch, Verlag Technik, 1969, S. 38, Tafel 2.4.
Johannes Volmer, Grundlagen, S. 185, Tafel 6.1.
Johannes Volmer, Koppelgetriebe, S. 29, Tafel 2.2.
Volmer, Lehrbuch', S. 39.
Volmer, Koppelgetriebe, S. 56
Volmer, Koppelgetriebe, S. 34
Volmer: Grundlagen, S. 39.
Siegfried Hildebrand: Feinmechanische Bauelemente, Hanser, München 1968, S. 633.
Volmer: Grundlagen, S. 33.
Klemmen wegen Fertigungsfehlern kann auch beim einfachen Parallelkurbelgetriebe in den Totlagen eintreten. Es wird ebenfalls als umlaufendes Getriebe benutzt (wobei die Totlagen mit bestimmten Hilfsmitteln überwunden werden).
Volmer: Grundlagen, S. 241.
Hildebrand, S. 627.
Volmer, Koppelgetriebe, S. 33/34
Volmer: Grundlagen, S. 327.
Hildebrand, S. 751.
Volmer: Grundlagen, S. 194.
Volmer: Koppelgetriebe, S. 25, S. 194.
Volmer: Grundlagen, S. 185.
Kurt Luck, Karl-Heinz Modler: Getriebetechnik: Analyse Synthese Optimierung, Springer, 1990, Seite 31, Tafel 2.2. Zusammenstellung von Grundgetrieben aus der Viergelenkkette
Volmer: Grundlagen, S. 185–188.
Dankert/ Dankert: Technische Mechanik. Doppelschwinge
Dankert/ Dankert: Technische Mechanik. Doppelkurbel
Luck/Modler, Seite 36, Tafel 2.4. Zusammenstellung von Grundgetrieben aus der Schubkurbelkette (eingeschränkte Vorschau in der Google-Buchsuche)
Volmer: Grundlagen, S. 188–192.
Dankert/ Dankert: Technische Mechanik. schwingende Kurbelschleife
Volmer: Grundlagen, S. 193.
Luck/Modler, Seite 38, Tafel 2.5. Zusammenstellung von Grundgetrieben aus der Kreuzschleifenkette
Volmer: Grundlagen, S. 192.
Luck/Modler, Seite 39, Tafel 2.6. Zusammenstellung von Grundgetrieben aus der Schubschleifenkette (eingeschränkte Vorschau in der Google-Buchsuche)
Hildebrandt, S. 639.
Volmer: Grundlagen, S. 323
Volmer: Grundlagen, S. 325
Volmer, 1978, S. 336 (eingeschränkte Vorschau in der Google-Buchsuche)
Volmer: Grundlagen, S. 54.
Volmer: Grundlagen, S. 124.
Volmer: Grundlagen, S. 90.
Volmer: Grundlagen, S. 219.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Johannes Volmer (Hrsg.): Getriebetechnik - Koppelgetriebe Verlag Technik, 1979, S. 24

[Vol13-2] Volmer: Koppelgetriebe, S. 13

[3] Johannes Volmer (Hrsg.): Getriebetechnik - Grundlagen Verlag Technik, 1995, ISBN 3-341-01137-4, S. 27

[4] Volmer, Koppelgetriebe, Seite 25. Am Anfang (19. Jahrh.) wurde des Viergelenkgetriebe noch Dreistabgetriebe genannt.

[5] Kerle u.A.: Getriebetechnik. Springer-Verlag, 2015, S. 10 (Volltext in der Google-Buchsuche).

[6] Volmer: Grundlagen S. 240

[7] Volmer: Grundlagen S. 241

[8] vgl. Volmer: Grundlagen, S. 184–185.

[Vol1-9] Volmer: Grundlagen, S. 184–185

[10] Dankert/ Dankert: Technische Mechanik. Beispiele für Koppelgetriebe inkl. animierter Darstellung von Koppelkurven tm-aktuell.de

[11] Volmer: Grundlagen, S. 195.

[12] Johannes Volmer: Getriebetechnik - Lehrbuch, Verlag Technik, 1969, S. 38, Tafel 2.4.

[13] Johannes Volmer, Grundlagen, S. 185, Tafel 6.1.

[14] Johannes Volmer, Koppelgetriebe, S. 29, Tafel 2.2.

[15] Volmer, Lehrbuch', S. 39.

[16] Volmer, Koppelgetriebe, S. 56

[17] Volmer, Koppelgetriebe, S. 34

[18] Volmer: Grundlagen, S. 39.

[19] Siegfried Hildebrand: Feinmechanische Bauelemente, Hanser, München 1968, S. 633.

[20] Volmer: Grundlagen, S. 33.

[21] Klemmen wegen Fertigungsfehlern kann auch beim einfachen Parallelkurbelgetriebe in den Totlagen eintreten. Es wird ebenfalls als umlaufendes Getriebe benutzt (wobei die Totlagen mit bestimmten Hilfsmitteln überwunden werden).

[22] Volmer: Grundlagen, S. 241.

[23] Hildebrand, S. 627.

[24] Volmer, Koppelgetriebe, S. 33/34

[25] Volmer: Grundlagen, S. 327.

[26] Hildebrand, S. 751.

[27] Volmer: Grundlagen, S. 194.

[28] Volmer: Koppelgetriebe, S. 25, S. 194.

[V136-29] Volmer: Grundlagen, S. 185.

[30] Kurt Luck, Karl-Heinz Modler: Getriebetechnik: Analyse Synthese Optimierung, Springer, 1990, Seite 31, Tafel 2.2. Zusammenstellung von Grundgetrieben aus der Viergelenkkette

[31] Volmer: Grundlagen, S. 185–188.

[32] Dankert/ Dankert: Technische Mechanik. Doppelschwinge

[33] Dankert/ Dankert: Technische Mechanik. Doppelkurbel

[34] Luck/Modler, Seite 36, Tafel 2.4. Zusammenstellung von Grundgetrieben aus der Schubkurbelkette (eingeschränkte Vorschau in der Google-Buchsuche)

[35] Volmer: Grundlagen, S. 188–192.

[36] Dankert/ Dankert: Technische Mechanik. schwingende Kurbelschleife

[37] Volmer: Grundlagen, S. 193.

[38] Luck/Modler, Seite 38, Tafel 2.5. Zusammenstellung von Grundgetrieben aus der Kreuzschleifenkette

[V192-39] Volmer: Grundlagen, S. 192.

[40] Luck/Modler, Seite 39, Tafel 2.6. Zusammenstellung von Grundgetrieben aus der Schubschleifenkette (eingeschränkte Vorschau in der Google-Buchsuche)

[41] Hildebrandt, S. 639.

[42] Volmer: Grundlagen, S. 323

[43] Volmer: Grundlagen, S. 325

[44] Volmer, 1978, S. 336 (eingeschränkte Vorschau in der Google-Buchsuche)

[95-54-45] Volmer: Grundlagen, S. 54.

[46] Volmer: Grundlagen, S. 124.

[47] Volmer: Grundlagen, S. 90.

[48] Volmer: Grundlagen, S. 219.