Momentanpol

Der Momentanpol ist bei einer ebenen Bewegung eines starren Körpers derjenige Raumpunkt, um den der Körper im Moment (Zeitpunkt, infinitesimal) als nur drehend angesehen und behandelt werden kann. Die Geschwindigkeit im Momentanpol ist im betrachteten Augenblick null oder wäre es, wenn sich der Starrkörper bis zum Momentanpol ausdehnte, siehe Bild.

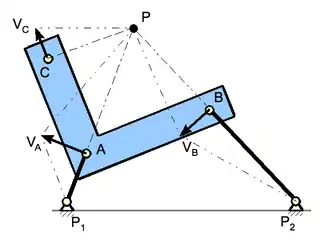
Koppelgetriebe: Der momentane Bewegungszustand der Koppel (blau), lässt sich auf eine Drehung um den Momentanpol P reduziereren. Die Geschwindigkeitsvektoren v in den Punkten A, B und C stehen senkrecht auf den Strahlen von P zu den Punkten, was P eindeutig bestimmt. Die Geschwindigkeit ist proportional zum Abstand zu P.

Werden die während einer Bewegung auftretenden Momentanpole markiert, entsteht im raumfesten Bezugssystem die Rastpolbahn und im Bezugssystem des bewegten Körpers die Gangpolbahn. Die Gangpolbahn rollt auf der Rastpolbahn gleitungslos ab.

Der Momentanpol ist eine in der Kinematik gebrauchte Abstraktion, mit der in der Getriebetechnik, der Robotik und bei der Auslegung von Radführungen von Automobilen gearbeitet wird.

Historisches

Die Existenz des momentanen Drehungszentrums hat Johann I Bernoulli 1742 entdeckt.[1] Der florentiner Mathematiker Giulio Mozzi[2] (1730–1813) untersuchte die Aufteilung einer Starrkörperbewegung in Translation und Rotation.[3] Michel Chasles formulierte 1878 die Sätze[4]

Die momentanen Normalen aller Bahnkurven gehen durch den Momentanpol.
Auch die Normalen der Einhüllenden aller Geraden und Kurven in ihren momentanen Berührungspunkten gehen durch den Momentanpol.
Jede Bewegung einer Ebene σ in σ' besteht im Abrollen einer Kurve p von einer Kurve p'.

Siehe Encyklopädie der mathematischen Wissenschaften.[5]

Konstruktion des Momentanpols

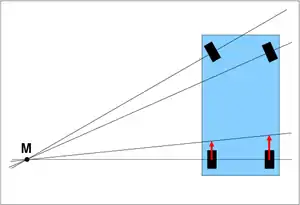
Wenn sich bei einem auf vier Rädern (schwarz) rollenden Starrkörper (blau) alle Radachsen im Momentanpol M treffen, kann sich der Körper ohne Gleiten der Räder in der Ebene bewegen.
Die Geschwindigkeitsvektoren der Hinterachsräder sind als rote Pfeile eingezeichnet.

Bei einer Rotation ist die Geschwindigkeit jedes Punktes senkrecht zur Verbindung dieses Punktes mit der Drehachse (Momentanpol). Der Momentanpol lässt sich bestimmen, wenn von zwei Punkten die Geschwindigkeiten bekannt sind.

Wenn beide Geschwindigkeiten in Betrag und Richtung gleich sind, handelt es sich um eine reine Translation, und der Momentanpol liegt im Unendlichen in Richtung der Senkrechten auf den beiden Geschwindigkeitsvektoren.
Wenn die Geschwindigkeitsrichtungen beider Punkte nicht parallel sind, wie bei den Radmitten der beiden Vorderräder im Bild, dann ist der Schnittpunkt der Senkrechten auf die Geschwindigkeitsvektoren in den beiden Punkten der Momentanpol.
Wenn die Geschwindigkeiten beider Punkte parallel sind, aber – wie bei den Hinterrädern im Bild – verschiedenen Betrag haben, ist der Momentanpol der Schnittpunkt der Verbindungslinie beider Punkte und der Verbindungslinie der Spitzen beider Geschwindigkeitsvektoren.

Alternativ zu dieser Konstruktion kann die Lage des Momentanpols auch berechnet werden, siehe Rastpol- und Gangpolbahn.

Definition

Jede Starrkörperbewegung lässt sich in eine Translation und eine Rotation zerlegen. Die Translation wird mit dem zeitabhängigen Bezugspunkt ${\vec {s}}(t)$ vorgegeben, für den sich jeder bewegte (oder auch ruhende) Punkt und auch der Schwerpunkt des Starrkörpers eignet. Die Rotation erfolgt um eine Drehachse, die in Richtung des Drehgeschwindigkeitsvektors ${\vec {\omega }}(t)$ weist, dessen Frobeniusnorm die Drehgeschwindigkeit angibt. Die Geschwindigkeit eines an einem Ort ${\vec {x}}$ befindlichen Partikels ist bei einer Starrkörperbewegung mit

{\vec {v}}({\vec {x}},t)={\dot {\vec {s}}}(t)+{\vec {\omega }}(t)\times {\bigl (}{\vec {x}}-{\vec {s}}(t){\bigr )}

gegeben. Das Rechenzeichen „×“ bildet das Kreuzprodukt und ${\dot {\vec {s}}}(t)$ ist die Geschwindigkeit des Bezugspunktes. Der Momentanpol ist nun ein Raumpunkt ${\vec {m}}(t)$ , in dem sich das Geschwindigkeitsfeld momentan als reine Drehung darstellt:

${\displaystyle {\vec {v}}({\vec {x}},t)={\dot {\vec {s}}}(t)+{\vec {\omega }}(t)\times {\bigl (}{\vec {x}}-{\vec {s}}(t){\bigr )}{\stackrel {\displaystyle$		(Definition)

Mit diesem Punkt sind auch alle Punkte auf der Geraden ${\vec {m}}+\lambda {\vec {\omega }}$ mit $\lambda \in \mathbb {R}$ Momentanpole. Skalare Multiplikation der Geschwindigkeit mit dem Drehgeschwindigkeitsvektor offenbart

{\vec {v}}({\vec {x}},t)\cdot {\vec {\omega }}(t)={\dot {\vec {s}}}(t)\cdot {\vec {\omega }}(t)={\vec {\omega }}(t)\cdot \left[{\vec {\omega }}(t)\times {\bigl (}{\vec {x}}-{\vec {m}}(t){\bigr )}\right]=0\,,

d. h. die Geschwindigkeit des Bezugspunktes muss senkrecht zur Drehachse sein, damit es einen Momentanpol geben kann. Momentan muss die Bewegung mithin – wie eingangs erwähnt – eine ebene sein.

Wenn die Drehgeschwindigkeit verschwindet, dann ist die Geschwindigkeit wegen ${\vec {v}}({\vec {x}},t)={\dot {\vec {s}}}(t)$ nicht vom Ort abhängig und daher gleichförmig. Die Definitionsgleichung

{\displaystyle {\vec {v}}({\vec {x}},t)={\dot {\vec {s}}}(t){\stackrel {\displaystyle

enthält dann gar keine Definition mehr und der Momentanpol ist mithin nicht definiert. Gelegentlich wird der Momentanpol bei einer gleichförmigen Bewegung in einen unendlich fernen Punkt auf der in der Ebene liegenden Senkrechten an die Bewegungsrichtung verschoben, was bei endlich ausgedehnten Starrkörpern probat ist.

Paradoxon des sich bewegenden Momentanpols

Der Momentanpol ist von der Zeit abhängig und kann daher durch den Raum wandern. Andererseits verschwindet jederzeit die Geschwindigkeit im Momentanpol:

{\vec {v}}({\vec {m}}(t),t)={\vec {\omega }}(t)\times {\bigl (}{\vec {m}}(t)-{\vec {m}}(t){\bigr )}={\vec {0}}\,,

was auch namensgebend für den Momentanpol ist. Wie kann sich aber etwas bewegen, das stillsteht?

Eine Ursache dieses scheinbaren Widerspruchs liegt in der Identifikation eines Partikels mit dem Raumpunkt, an dem es sich befindet. Das mit eulerscher Betrachtungsweise formulierte Geschwindigkeitsfeld ${\vec {v}}({\vec {x}},t)$ gibt die Geschwindigkeit eines sich im Ort ${\vec {x}}$ befindlichen Partikels an und entsprechend ist ${\vec {v}}({\vec {m}},t)$ die Geschwindigkeit des im Momentanpol stillstehenden Partikels. Der Momentanpol ist aber nicht dieses Partikel, sondern nur der geometrische Ort, an dem es sich befindet. Der Momentanpol ist – genauso wie der Bezugspunkt oder die Drehachse – ein Parameter der Bewegung, der ein geometrisches Objekt repräsentiert. Der Momentanpol verweist wie ein Zeiger auf einen Raumpunkt und in diesem Raumpunkt herrscht, sofern sich dort etwas befindet, Stillstand. Dieser Raumpunkt muss auch nicht notwendigerweise im Starrkörper liegen. Der Momentanpol ist also nicht an Partikel gebunden und kann fließend durch die Ebene schweifen solange die Partikel im Momentanpol nur augenblicklich anhalten (Wenn ein Partikel stehen bleibt, dann befindet sich dort genauso solange auch der Momentanpol).

Eine zweite Ursache des Paradoxons liegt in den unterschiedlichen Bewegungsweisen der Partikel und des Momentanpols begründet. In der klassischen Mechanik ist der Raum absolut, unveränderlich und unbeeinflusst von den physikalischen Vorgängen und entsprechend können sich Raumpunkte im mechanischen Sinn nicht bewegen, sondern nur im mathematischen. Während sich also die Partikel im mechanischen Sinn bewegen, bewegt sich der Momentanpol im mathematischen Sinn. Der Momentanpol ist eine Funktion der Zeit, die einen Raumpunkt ausgibt. Wenn der Momentanpol nicht stillsteht, dann sind zu jedem Zeitpunkt – wenn überhaupt – andere Partikel am Ort des Momentanpols. Aus mechanischer Sicht ist eine Folge von Momentanpolen bei einer Bewegung eine Alternative zur paradoxen Vorstellung eines sich bewegenden Momentanpols.

Alle Partikel des Starrkörpers, die jemals in einem Momentanpol zum Stehen kommen, liegen auf der Gangpolbahn während die Rastpolbahn die Menge aller Raumpunkte ist, die irgendwann Momentanpol sind. Die Gangpolbahn rollt gleitungslos auf der Rastpolbahn ab, weil die Polwechselgeschwindigkeiten auf der Rastpolbahn und der Gangpolbahn gleich groß sind. Im Momentanpol wechseln sich die Raumpunkte ebenso schnell einander ab wie die Partikel des Starrkörpers (sofern sich der Momentanpol im Starrkörper befindet).

Beispiel: Rollendes Rad

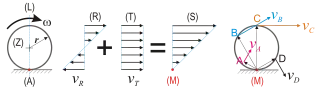
Beispiel Rad: Momentanpol (M hier M=A) an einem Rad, welches an einem Fahrzeug montiert ist

Das im Bild gezeigte Rad an einem Fahrzeug besitzt aus Sicht der Kinematik mehrere Eigenschaften, wenn man es entlang der gestrichelten Linie durch das Drehzentrum (Z) und den Aufstandspunkt (A) betrachtet:

Da es am Fahrzeug befestigt ist, nimmt es an dessen translatorischer Bewegung teil. Dieser Anteil wird durch die Geschwindigkeitspfeile (T) entlang der Linie (L) dargestellt.
Ein Beobachter im Zentrum (Z) sieht, dass sich das Rad (im Gegensatz zum Fahrzeug) zusätzlich um dieses Zentrum (Z) dreht. Dieser Anteil wird durch die Pfeile (R) der Tangentialgeschwindigkeiten entlang der Linie (L) dargestellt.
Solange das Rad abrollt, hat es im Aufstandspunkt (A) die Geschwindigkeit 0, denn die Straße steht und das Rad rutscht an diesem Punkt nicht über die Straße und schlupft in dieser idealisierten Betrachtung auch nicht.

Die Überlagerung der Geschwindigkeiten (R) und (T) sowie die Bedingung, dass der Punkt am Rad, der gerade Aufstandspunkt (A) auf der stehenden Straße ist, selbst auch stehen muss, macht den Aufstandspunkt (A) gleichzeitig zum Momentanpol (M) der Radbewegung.

Die rechte Darstellung zeigt, wie man mit Hilfe des Momentanpols (M) an vier beispielhaft gewählten Punkten A–D die momentane Geschwindigkeit ermitteln kann: Sie ist das Produkt aus der Winkelgeschwindigkeit ω um den Momentanpol (M, dieselbe Winkelgeschwindigkeit wie um Z) und dem Abstand des jeweiligen Punktes (im Beispiel A…D) vom Momentanpol (M). Sucht man beispielsweise den Punkt des Rades, der vom Momentanpol am weitesten entfernt ist, so hat man den Punkt mit der höchsten Geschwindigkeit gefunden.

Die Rastpolbahn ist in diesem Beispiel die Straße, denn aus Sicht eines Beobachters an der Straße liegen alle Momentanpole auf der Fahrbahn. Die Gangpolbahn ist aus Sicht eines Beobachters auf dem Rad der Umfang.

Der Momentanpol soll nun auch berechnet werden. Gegeben sei ein kartesisches Koordinatensystem mit zueinander senkrechten x-, y- und z-Richtungen und zugehöriger Standardbasis ${\vec {e}}_{x,y,z}$ . Die x-Achse stellt die Straße dar, auf der das Rad im Ursprung der x-y-Ebene zur Zeit t=0 beginnt zu rollen. Das Rad besitze den Radius R und eine gleichförmige Drehgeschwindigkeit ω=-Ω < 0 um die z-Achse und rollt auf der x-Achse somit in positive x-Richtung. Der Achsmittelpunkt befindet sich dann in der Höhe R über der x-Achse und soll sich parallel zur x-Achse bewegen. Aus Sicht des Achsmittelpunktes hat ein auf dem Radumfang befindliches Partikel P die Geschwindigkeit $\Omega \,R$ und dieselbe Geschwindigkeit hat der Achsmittelpunkt umgekehrt aus der Sicht dieses Partikels P. Der Aufstandspunkt A des Rades auf der x-Achse ist ein solches Partikel. Der Achsmittelpunkt ${\vec {s}}(t)$ und seine Geschwindigkeit sind entsprechend mit

{\vec {s}}(t=0)=R{\vec {e}}_{y}\;\wedge \;{\dot {\vec {s}}}(t)=\Omega R{\vec {e}}_{x}\quad \leftrightarrow \quad {\vec {s}}(t)=\Omega Rt{\vec {e}}_{x}+R{\vec {e}}_{y}

gegeben. Das Geschwindigkeitsfeld lautet mithin:

{\begin{aligned}{\vec {v}}(x,y,t)=&\Omega R{\vec {e}}_{x}-\Omega {\vec {e}}_{z}\times (x{\vec {e}}_{x}+y{\vec {e}}_{y}-\Omega Rt{\vec {e}}_{x}-R{\vec {e}}_{y})\\=&-\Omega {\vec {e}}_{z}\times (R{\vec {e}}_{y}+x{\vec {e}}_{x}+y{\vec {e}}_{y}-\Omega Rt{\vec {e}}_{x}-R{\vec {e}}_{y})\\=&-\Omega {\vec {e}}_{z}\times (x{\vec {e}}_{x}+y{\vec {e}}_{y}-\underbrace {\Omega Rt{\vec {e}}_{x}} _{={\vec {m}}(t)})\end{aligned}}

woraus also sofort ${\vec {m}}(t)=\Omega Rt{\vec {e}}_{x}$ folgt. Das ergibt sich auch mit der im Artikel zur Rastpolbahn angegebenen Formel:

{\begin{aligned}x_{M}=&x_{S}-{\frac {v_{Sy}}{\omega }}=\Omega Rt-{\frac {0}{-\Omega }}=\Omega Rt\\y_{M}=&y_{S}+{\frac {v_{Sx}}{\omega }}=R+{\frac {\Omega R}{-\Omega }}=0\end{aligned}}

Siehe auch

Einzelnachweise

Johann I Bernoulli: Die Werke. Vierter Band. Marci-Michaelis Bousquet & Sociorum, Lausanne und Genf 1742, XIV De Centro Spontaneo rotationis, S. 265 ff. (Latein, eingeschränkte Vorschau in der Google-Buchsuche [abgerufen am 27. Dezember 2020] Originaltitel: Opera Omnia.).
Giulio Giuseppe Mozzi. Wikipedia, 25. Januar 2020, abgerufen am 15. April 2020 (italienisch).
Giulio Giuseppe Mozzi: Mathematischer Diskurs über die momentane Rotation von Körpern. Druckerei von Donato Campo, Neapel 1763 (italienisch, archive.org [abgerufen am 27. Dezember 2020] Originaltitel: Discorso matematico sopra il rotamento mementaneo dei corpi. Zitiert nach Marcolongo (1911), S. 122.).
M. Chasles: Geometrische Abhandlung über die Konstruktion von Normalen an mehrere mechanische Kurven. In: Bulletin de la Société Mathématique de France. Band 6, 1878, S. 208–250 (französisch, numdam.org [abgerufen am 27. Dezember 2020] Originaltitel: Mémoire de géométrie sur la construction des normales à plusieurs courbes mécaniques.).
Felix Klein und Conrad Müller: Encyklopädie der mathematischen Wissenschaften. Mechanik. 4. Band, 1. Teilband. B. G. Teubner, Leipzig 1908, S. 210 ff. (archive.org [abgerufen am 27. Dezember 2020]).

Literatur

M. Husty: Kinematik und Robotik. Springer, 2012, ISBN 978-3-642-63822-0.
K. Luck, K.-H. Modler: Getriebetechnik: Analyse Synthese Optimierung. Springer, 1990, ISBN 978-3-211-82147-3.
Ulrich Gabbert, Ingo Raecke: Technische Mechanik für Wirtschaftsingenieure. HANSER_VERLAG, 2007 ISBN 3-446-41409-6
Rolf Mahnken: Lehrbuch der Technischen Mechanik. Grundlagen und Anwendungen. 2. Auflage. Band 1: Starrkörperstatik. Springer Vieweg, Berlin, Heidelberg 2016, ISBN 978-3-662-52784-9.
Roberto Marcolongo: Theoretische Mechanik. B. G. Teubner, Leipzig und Berlin 1911, S. 132 ff. (archive.org [abgerufen am 28. Dezember 2020]).

Weblinks

Momentanpol bei einer Koppel (68,1 MB; .avi), Video einer Animation des Instituts für Angewandte Mechanik, TU München

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Johann I Bernoulli: Die Werke. Vierter Band. Marci-Michaelis Bousquet & Sociorum, Lausanne und Genf 1742, XIV De Centro Spontaneo rotationis, S. 265 ff. (Latein, eingeschränkte Vorschau in der Google-Buchsuche [abgerufen am 27. Dezember 2020] Originaltitel: Opera Omnia.).

[2] Giulio Giuseppe Mozzi. Wikipedia, 25. Januar 2020, abgerufen am 15. April 2020 (italienisch).

[3] Giulio Giuseppe Mozzi: Mathematischer Diskurs über die momentane Rotation von Körpern. Druckerei von Donato Campo, Neapel 1763 (italienisch, archive.org [abgerufen am 27. Dezember 2020] Originaltitel: Discorso matematico sopra il rotamento mementaneo dei corpi. Zitiert nach Marcolongo (1911), S. 122.).

[4] M. Chasles: Geometrische Abhandlung über die Konstruktion von Normalen an mehrere mechanische Kurven. In: Bulletin de la Société Mathématique de France. Band 6, 1878, S. 208–250 (französisch, numdam.org [abgerufen am 27. Dezember 2020] Originaltitel: Mémoire de géométrie sur la construction des normales à plusieurs courbes mécaniques.).

[5] Felix Klein und Conrad Müller: Encyklopädie der mathematischen Wissenschaften. Mechanik. 4. Band, 1. Teilband. B. G. Teubner, Leipzig 1908, S. 210 ff. (archive.org [abgerufen am 27. Dezember 2020]).