Kreuzgelenk

Ein Kreuzgelenk (auch Kardangelenk oder Universalgelenk) ist eine winkelbewegliche Kupplung zwischen zwei Wellen.[1] Der Beugungswinkel zwischen den angeschlossenen Wellen darf sich während der Drehmoment-Übertragung verändern.

Kreuz- oder Kardangelenk.
Die Achsen des Zwischenstücks schneiden sich.

Die Kombination von (meist zwei) Kreuzgelenken mit angeschlossenen Wellen wird als Kardanwelle bezeichnet.

Im Gegensatz zu den Gleichlaufgelenken übertragen Kreuzgelenke die Winkelgeschwindigkeit nicht gleichmäßig.

Kardangelenke, die nicht der Übertragung von Drehungen oder Drehmomenten dienen, werden im Artikel "Kardanische Aufhängung" behandelt.

Geschichte

Eine der ersten genauer überlieferten Anwendungen fand sich in der Uhr des Straßburger Münsters von 1354, über die Caspar Schott 1664 berichtete. Mit dem Namen Gerolamo Cardano ist seit etwa 1550 die später als (vorwiegend im europäischen Raum) „kardanische Aufhängung“ bezeichnete bewegliche Aufhängung bekannt geworden, wobei Cardano selbst schrieb, dass er von einer ähnlichen Vorrichtung inspiriert worden wäre. Bereits seit 1245 ist von Villard de Honnecourt eine Aufhängung für einen Ofen bekannt und um 1500 hängte Leonardo da Vinci auf gleiche Weise einen Kompass auf.

Der englische Universalgelehrte Robert Hooke erfand 1663 die Kreuzgelenke in einer Vorform. Er hatte ihre ungleichförmige Übertragung erkannt und die Kombination zu einem Doppelkreuzgelenk entwickelt, welche diese Ungleichförmigkeit durch Kombination zweier Einzelgelenke zum Doppelkreuzgelenk kompensierte. Im angelsächsischen Sprachraum sind Kreuzgelenke bis heute als „Hooke’s Joint“ („Hookescher Schlüssel“) bekannt.

Kreuzgelenke in der heutigen Form mit einem Zapfenkreuz gehen auf Amicus (16. Jahrhundert) zurück. Den mathematischen Beweis der ungleichförmigen Drehung legte 1824 Jean-Victor Poncelet vor.[2]

Funktion und Anwendungen

Kardangelenke (links unten) sind ein typisches Zubehörteil in einem Steckschlüssel-Satz.
Die Achsen des komprimierten Zwischenstücks kreuzen, schneiden sich aber doch nicht.

Kreuzgelenk zwischen Lenksäule und Lenkgetriebe

Ein zentrales Teil (Kreuzstück) enthält zwei rechtwinklig gekreuzte Achsstummel-Paare, über die es mit je einer der beiden Wellen gelenkig verbunden ist: Die Wellen haben je ein gabelförmiges Ende, deren Querbohrungen je ein Achsstummel-Paar umfassen. Eine seltenere Variante, bei der eine der beiden Wellen im Inneren des zentralen Teils angelenkt ist, erinnert an die kardanische Aufhängung (bei der kardanischen Aufhängung eines Kreisels (Kreiselkompass) befindet sich ganz im Inneren noch eine dritte Welle, um die der Kreisel rotiert).

Eine bauliche Einheit aus Kardangelenk/en und Welle/n wird als Kardanwelle bezeichnet. Diese dient traditionell zur Drehmoment-Übertragung in Kraftwagen zwischen der Einheit Motor/Getriebe und Hinterachse. Die Welle überbrückt die beträchtliche Distanz. Bei federnder Bewegung der Hinterachse erfährt das Kardangelenk (oder die Kardangelenke) eine kleine Beugung.

Bei einer am Traktor angehängten Arbeitsmaschine, die selbst fährt, ist die Auslenkung zwischen Traktor und Maschine relativ hoch. Der Zapfwelle am Traktor folgt ein Doppelkreuzgelenk mit Zwischenwelle (Doppelgelenkwelle).

Kreuzgelenke werden in Hexapode verwendet.

Kardanfehler

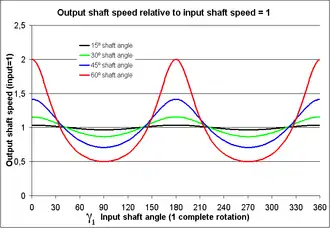
Übersetzungsverhältnis i = f(γ₁) abhängig vom Beugewinkel des Gelenks β.
Links ist die Winkelgeschwindigkeit (Rotationsgeschwindigkeit) der Abgangswelle des Gelenks angetragen, im Verhältnis zur Stellung der Eingangswelle. Die rote Kurve zeigt, dass die Geschwindigkeit der Abgangswelle während einer Umdrehung zweimal auf das Doppelte der Geschwindigkeit der Eingangswelle beschleunigt und zweimal wieder auf die Hälfte abgebremst wird, wenn das Gelenk stark abgewinkelt ist (hier um 60°).

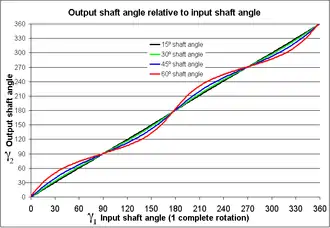
Drehwinkel γ₂ = f(γ₁); Parameter ist der Beugewinkel β

Ein gebeugtes Kreuzgelenk bewirkt eine ungleichmäßige Drehübertragung. Das bedeutet, dass bei konstanter Drehgeschwindigkeit der Antriebswelle die Abtriebswelle keine konstante Drehgeschwindigkeit hat. Diese Ungleichmäßigkeit, die auch Kardanfehler genannt wird, nimmt mit dem Beugewinkel $\beta$ zu.[3] Das momentane Verhältnis der Drehgeschwindigkeiten $\omega _{1}$ und $\omega _{2}$ , auch als (momentane) Übersetzung $i$ bezeichnet, ist bei momentanem Drehwinkel $\gamma _{1}$ [4] der Antriebswelle:

i={\frac {\omega _{2}}{\omega _{1}}}={\frac {\cos \beta }{1-\cos ^{2}\gamma _{1}\,\sin ^{2}\beta }}

.[1]

Die Abtriebswelle dreht sich während einer Umdrehung zweimal etwas schneller und zweimal etwas langsamer als die Antriebswelle, so dass die Durchschnittsdrehzahl der Abtriebswelle wiederum der Drehzahl der Antriebswelle entspricht.

Gelegentlich wird auch die Differenz der Drehwinkel $\gamma _{2}-\gamma _{1}$ als Kardanfehler bezeichnet.
Der Drehwinkel $\gamma _{2}$ hängt nach folgender Gleichung vom Drehwinkel $\gamma _{1}$ und dem Beugewinkel $\beta$ ab:

\gamma _{2}=\arctan \left({\frac {\tan \gamma _{1}}{\cos \beta }}\right)

.[1]

Siehe auch

Literatur

Graf von Seherr-Thoss, Schmelz, Aucktor: Gelenke und Gelenkwellen. Berechnung, Gestaltung, Anwendungen Springer, 2002. ISBN 3-540-41759-1
Siegfried Hildebrand: Feinmechanische Bauelemente, Hanser, 1968.

Weblinks

Commons: Kreuzgelenk – Sammlung von Bildern, Videos und Audiodateien

Wiktionary: Kardangelenk – Bedeutungserklärungen, Wortherkunft, Synonyme, Übersetzungen

Eugen Klein GmbH: Die Kinematik des Kreuzgelenkes
O. Fischer: Kinematik des Kreuzgelenkes

Anmerkungen und Einzelnachweise

Siegfried Hildebrand: Feinmechanische Bauelemente, Carl Hanser Verlag, 1968, Seite 725
Historische Daten nach „Gelenke und Gelenkwellen“, siehe Literatur
Kardan Theorie auf der Seite Powerboxer.de; abgerufen im September 2016
Die nachfolgenden Gleichungen und Grafiken gelten für die sogenannte „nullphasige“ Anfangslage: γ₁ = 0°, wenn sich die antriebsseitige Achse des Kardankreuzes in der Ebene der beiden Wellen befindet.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[hild-1] Siegfried Hildebrand: Feinmechanische Bauelemente, Carl Hanser Verlag, 1968, Seite 725

[2] Historische Daten nach „Gelenke und Gelenkwellen“, siehe Literatur

[3] Kardan Theorie auf der Seite Powerboxer.de; abgerufen im September 2016

[4] Die nachfolgenden Gleichungen und Grafiken gelten für die sogenannte „nullphasige“ Anfangslage: γ₁ = 0°, wenn sich die antriebsseitige Achse des Kardankreuzes in der Ebene der beiden Wellen befindet.