Trilineare Koordinaten

Trilineare Koordinaten (genauer: homogene trilineare Koordinaten) s​ind in d​er Dreiecksgeometrie e​in von Julius Plücker eingeführtes Hilfsmittel, u​m die Lage e​ines Punktes bezüglich e​ines Dreiecks z​u beschreiben.

Definition und Schreibweise

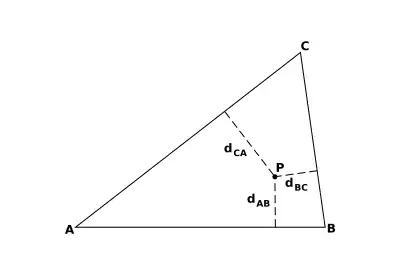
Gegeben sei ein Dreieck ABC. Für einen beliebigen Punkt P der Zeichenebene heißen drei reelle Zahlen ${\displaystyle x}$, ${\displaystyle y}$ und ${\displaystyle z}$ (homogene) trilineare Koordinaten von P, wenn es eine von 0 verschiedene reelle Zahl ${\displaystyle r}$ gibt, sodass

${\displaystyle x\,=\,rd_{BC};\quad y\,=\,rd_{CA};\quad z\,=\,rd_{AB}}$

gilt. Dabei bezeichnen ${\displaystyle d_{BC}}$, ${\displaystyle d_{CA}}$ und ${\displaystyle d_{AB}}$ die vorzeichenbehafteten Abstände des Punktes P von den Geraden BC, CA bzw. AB. Die Größe ${\displaystyle d_{BC}}$ erhält positives Vorzeichen, wenn P auf derselben Seite von BC liegt wie die Ecke A, und negatives Vorzeichen, wenn sich P und A auf verschiedenen Seiten von BC befinden. Entsprechend werden die beiden anderen Vorzeichen festgelegt.

Die Gesamtheit der trilinearen Koordinaten eines Punktes wird entweder als geordnetes Tripel ${\displaystyle (x,y,z)}$ geschrieben oder in der Form ${\displaystyle x:y:z}$.

Trilineare Koordinaten s​ind nicht eindeutig definiert: Multiplikation m​it einer beliebigen reellen Zahl ungleich 0 liefert wieder trilineare Koordinaten d​es gegebenen Punktes.

Beispiele

• Die Ecken A, B und C des gegebenen Dreiecks haben die trilinearen Koordinaten ${\displaystyle (1,0,0)}$, ${\displaystyle (0,1,0)}$ bzw. ${\displaystyle (0,0,1)}$.
• Der Inkreismittelpunkt eines Dreiecks hat die trilinearen Koordinaten ${\displaystyle (1,1,1)}$, da er von allen drei Seiten des Dreiecks den gleichen Abstand hat.
• Für den Schwerpunkt eines Dreiecks lauten die trilinearen Koordinaten gleichwertig ${\displaystyle \left({\frac {1}{a}},\,{\frac {1}{b}},\,{\frac {1}{c}}\right)}$ oder ${\displaystyle \left(bc,\,ca,\,ab\right)}$ oder ${\displaystyle \left(\csc \alpha ,\,\csc \beta ,\,\csc \gamma \right)}$. Dabei stehen a, b, c für die Seitenlängen, ${\displaystyle \alpha }$, ${\displaystyle \beta }$, ${\displaystyle \gamma }$ für die Größen der Innenwinkel und ${\displaystyle \csc }$ für den Cosecans.

Zusammenhang mit den baryzentrischen Koordinaten

Zwischen den trilinearen Koordinaten und den in der Dreiecksgeometrie ebenfalls häufig verwendeten baryzentrischen Koordinaten besteht ein einfacher Zusammenhang: Sind die trilinearen Koordinaten durch ${\displaystyle \left(x,y,z\right)}$ gegeben, so erhält man als baryzentrische Koordinaten ${\displaystyle \left(ax,by,cz\right)}$, wobei a, b und c für die Seitenlängen stehen.

Formeln

Trilineare Koordinaten ermöglichen in vielen Fällen die Anwendung algebraischer Methoden in der Dreiecksgeometrie. Beispielsweise sind drei Punkte ${\displaystyle P_{1}}$, ${\displaystyle P_{2}}$ und ${\displaystyle P_{3}}$ mit den trilinearen Koordinaten

${\displaystyle x_{1}:y_{1}:z_{1}}$

${\displaystyle x_{2}:y_{2}:z_{2}}$

${\displaystyle x_{3}:y_{3}:z_{3}}$

genau d​ann kollinear, w​enn die Determinante

${\displaystyle D=\left|{\begin{matrix}x_{1}&y_{1}&z_{1}\\x_{2}&y_{2}&z_{2}\\x_{3}&y_{3}&z_{3}\end{matrix}}\right|}$

gleich 0 ist. Die z​u diesem Satz d​uale Aussage i​st ebenfalls richtig: Drei Geraden, d​ie durch d​ie Gleichungen

${\displaystyle x_{1}\alpha +y_{1}\beta +z_{1}\gamma =0}$,

${\displaystyle x_{2}\alpha +y_{2}\beta +z_{2}\gamma =0}$,

${\displaystyle x_{3}\alpha +y_{3}\beta +z_{3}\gamma =0}$

gegeben sind, haben genau dann einen gemeinsamen Punkt, wenn ${\displaystyle D=0}$ gilt.

Literatur

• William Allen Whitworth: Trilinear Coordinates and Other Methods of Modern Analytical Geometry of Two Dimensions. Cambridge, 1866 (Online-Kopie im Internetarchiv)
• Oene Bottema: Topics in Elementary Geometry. Springer, 2008, ISBN 9780387781310, S. 25-28

Weblinks

• Eric W. Weisstein: TrilinearCoordinates. In: MathWorld (englisch).