Konfokale Kegelschnitte
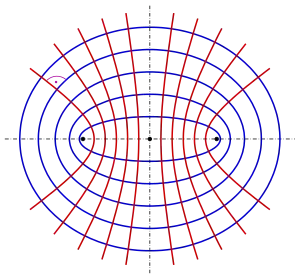
In der Geometrie heißen zwei Kegelschnitte konfokal, wenn sie die gleichen Brennpunkte besitzen. Da Ellipsen und Hyperbeln jeweils zwei Brennpunkte besitzen, gibt es konfokale Ellipsen, konfokale Hyperbeln und konfokale Ellipsen und Hyperbeln. Konfokale Ellipsen und Hyperbeln haben die bemerkenswerte Eigenschaft: Jede Ellipse schneidet jede Hyperbel senkrecht (s. unten). Parabeln besitzen jeweils nur einen Brennpunkt. Konfokale Parabeln haben den gleichen Brennpunkt und die gleiche Symmetrieachse. Durch diese Konvention gehen durch jeden Punkt, der nicht auf der Symmetrieachse liegt, genau zwei konfokale Parabeln, die sich senkrecht schneiden (s. unten).
Eine formale Fortsetzung des Konzepts der konfokalen Kegelschnitte auf Flächen führt auf die konfokalen Quadriken.
Konfokale Ellipsen
Eine Ellipse, die kein Kreis ist, ist durch ihre zwei Brennpunkte und einen Punkt, der nicht auf der Strecke zwischen den Brennpunkten liegt, eindeutig bestimmt (s. Definition einer Ellipse). Die Schar der konfokalen Ellipsen mit den Brennpunkten lässt sich durch die Gleichung
mit dem Scharparameter beschreiben. (Die lineare Exzentrizität und der Mittelpunkt sind durch die Brennpunkte eindeutig bestimmt.) Da ein Ellipsenpunkt den Scharparameter eindeutig bestimmt, gilt:
- Zwei beliebige Ellipsen dieser Schar schneiden sich nicht.
Eine geometrische Figur, die von zwei konfokalen Ellipsen berandet wird, nennt man 2-dimensionales Fokaloid.
Konfokale Hyperbeln
Eine Hyperbel ist durch ihre zwei Brennpunkte und einen Punkt, der nicht auf der Nebenachse und nicht auf der Hauptachse außerhalb der Strecke liegt, eindeutig bestimmt (s. Definition einer Hyperbel). Die Schar der konfokalen Hyperbeln mit den Brennpunkten lässt sich durch die Gleichung
mit dem Scharparameter beschreiben. (Die lineare Exzentrizität ist durch die Brennpunkte eindeutig bestimmt.) Da ein Hyperbelpunkt den Scharparameter eindeutig bestimmt, gilt:
- Zwei beliebige Hyperbeln dieser Schar schneiden sich nicht.
Konfokale Ellipsen und Hyperbeln
Gemeinsame Beschreibung
Aus den obigen Darstellungen der konfokalen Ellipsen und Hyperbeln ergibt sich eine gemeinsame Darstellung: Die Gleichung
beschreibt eine Ellipse, falls und eine Hyperbel, falls ist.
Eine weitere in der Literatur[1] übliche Darstellung ist:
Dabei sind die Halbachsen einer vorgegebenen Ellipse (damit sind auch die Brennpunkte gegeben) und der Scharparameter.
Für erhält man konfokale Ellipsen (es ist ) und
für konfokale Hyperbeln mit den gemeinsamen Brennpunkten .
Grenzkurven
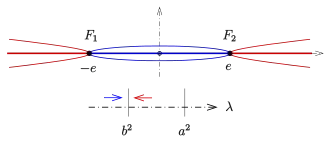
An der Stelle hat die Schar als linksseitige Grenzkurve (unendlich dünne Ellipse) die Strecke auf der x-Achse und als rechtsseitige Grenzkurve (unendlich dünne Hyperbel) die beiden Strahlen . Also:
- Die beiden Grenzkurven an der Stelle haben die beiden Brennpunkte gemeinsam.
Diese Eigenschaft findet im 3-dimensionalen Fall (s. u.) ihr Analogon und führt zur Definition der (unendlich vielen) Brennpunkte, Fokalkurven genannt, von konfokalen Quadriken.
An der Stelle hat die Schar als linksseitige Grenzkurve eine unendlich steile Hyperbel, bei der beide Äste auf die y-Achse fallen. Eine rechtsseitige Genzkurve gibt es hier nicht, da für die Kegelschnittgleichung keine Lösungen besitzt.
Zweifaches Orthogonalsystem
Betrachtet man die zu zwei Brennpunkten gehörige Ellipsen- und Hyperbelschar (s. erstes Bild), so folgt aus der jeweiligen Brennpunktseigenschaft (Die Tangente einer Ellipse halbiert den Außenwinkel der Brennstrahlen, die Tangente einer Hyperbel halbiert den Winkel der Brennstrahlen.):
- Jede Ellipse der Schar schneidet jede Hyperbel der Schar senkrecht (s. Bild).
Diese Aussage lässt sich auch rechnerisch beweisen, indem man die Ellipsen und Hyperbeln als implizite Kurven auffasst und mit Hilfe partieller Ableitungen Normalenvektoren in den Schnittpunkten (s. Abschnitt Satz von Ivory) berechnet.
Die Ebene lässt sich also mit einem orthogonalen Netz aus konfokalen Ellipsen und Hyperbeln überziehen.
Das orthogonale Netz von konfokalen Ellipsen und Hyperbeln ist die Grundlage der elliptischen Koordinaten.
Konfokale Parabeln

Parabeln besitzen jeweils nur einen Brennpunkt. Eine Parabel lässt sich als eine Grenzkurve einer Ellipsenschar (Hyperbelschar) auffassen, bei der ein Brennpunkt festgehalten wird und der zweite ins Unendliche wandert. Führt man diesen Grenzübergang für ein Netz von Ellipsen und Hyperbeln (s. 1. Bild) durch, so erhält man ein Netz aus zwei Scharen konfokaler Parabeln.
Verschiebt man die Parabel mit der Gleichung um in -Richtung, erhält man die Gleichung einer Parabel mit dem Ursprung als Brennpunkt. Es gilt:
- sind nach rechts geöffnete Parabeln und
- sind nach links geöffnete Parabeln
- mit dem gemeinsamen Brennpunkt
Anhand der Leitlinien-Definition einer Parabel erkennt man:
- Die nach rechts (links) geöffneten Parabeln schneiden sich nicht.
Man rechnet nach:
- Jede nach rechts geöffnete Parabel schneidet jede nach links geöffnete Parabel in den beiden Punkten senkrecht (s. Bild).
( sind Normalenvektoren in den Schnittpunkten. Ihr Skalarprodukt ist .)
Die Ebene lässt sich also (analog zu konfokalen Ellipsen und Hyperbeln) mit einem orthogonalen Netz aus konfokalen Parabeln überziehen.
Bemerkung: Das Netz aus konfokalen Parabeln lässt sich auffassen als das Bild eines achsenparallelen Netzes der rechten Halbebene unter der konformen Abbildung der komplexen Ebene (s. Weblink).
Parabolische Koordinaten:
Jeder Punkt der oberen Halbebene ist der Schnittpunkt zweier konfokaler Parabeln
. Führt man neue Parameter so ein, dass ist, so erhält man für den Schnittpunkt (s. o.):
heißen parabolische Koordinaten des Punktes (siehe parabolische Zylinderkoordinaten).
Satz von Graves: Fadenkonstruktion konfokaler Ellipsen
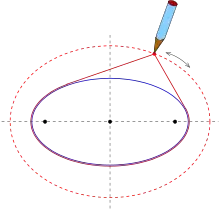
1850 hat der irische Bischof von Limerick Charles Graves (en) die folgende Fadenkonstruktion einer zu einer gegebenen Ellipse konfokalen Ellipse angegeben und bewiesen:[2]
- Schlingt man um eine gegebene Ellipse E einen geschlossenen Faden, der länger als der Umfang von E ist, und zeichnet wie bei der Gärtner-Konstruktion einer Ellipse eine Kurve (s. Bild), so ist diese Kurve eine zu E konfokale Ellipse.
Der Beweis dieses Satzes verwendet elliptische Integrale und ist in dem Buch von Felix Klein enthalten. Otto Staude hat diese Methode zur Konstruktion konfokaler Ellipsoide verallgemeinert (s. Buch von F. Klein).
Artet die gegebene Ellipse zu der Strecke zwischen den beiden Brennpunkten aus, erhält man eine Variante der Gärtnerkonstruktion einer Ellipse: Man schlingt dann einen geschlossenen Faden der Länge um die Brennpunkte.
Konfokale Quadriken

(rot), (blau), (lila)
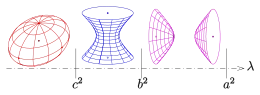
Definition
Unter konfokalen Quadriken versteht man eine formale Fortsetzung des Konzepts der konfokalen Kegelschnitte in den 3-dimensionalen Raum[3]:
Es seien mit fest gewählt. Dann beschreibt die Gleichung
- für ein Ellipsoid,
- für ein einschaliges Hyperboloid (im Bild blau),
- für ein zweischaliges Hyperboloid.
- Für hat die Gleichung keine Lösung.
Fokalkurven
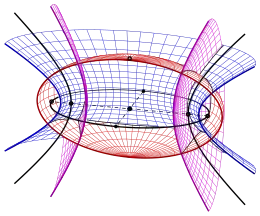
(Ellipsoid, rot), (1sch. Hyperb., blau),
(1sch. Hyperb., blau), (2sch. Hyperb., lila)
unten: Grenzflächen zwischen den Typen
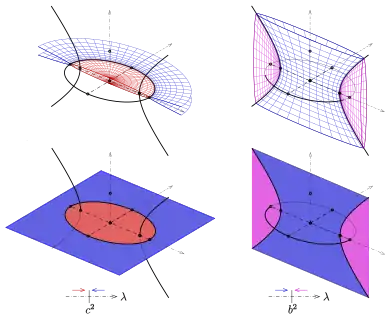
Grenzflächen für :
Lässt man in der Schar der Ellipsoide () den Scharparameter (von unten !) gegen laufen, erhält man ein "unendlich flaches" Ellipsoid, genauer: das Gebiet in der x-y-Ebene, das aus der Ellipse mit der Gleichung
und deren doppelt belegtem Inneren (im Bild unten, dunkelrot) besteht.
Lässt man in der Schar der einschaligen Hyperboloide () den Scharparameter (von oben !) gegen laufen, erhält man ein "unendlich flaches" Hyperboloid, genauer: das Gebiet in der x-y-Ebene, das aus derselben Ellipse und deren doppelt belegtem Äußeren (im Bild unten, blau) besteht. D.h.:
Die beiden Grenzflächen an der Stelle haben die Ellipse
gemeinsam.
Grenzflächen für :
Analoge Überlegungen an der Stelle ergeben:
Die beiden Grenzflächen (im Bild unten rechts, blau und lila) an der Stelle haben die Hyperbel
gemeinsam.
Fokalkurven:
Man prüft leicht nach, dass die Brennpunkte der Ellipse die Scheitel der Hyperbel und umgekehrt sind. D.h.: Ellipse und Hyperbel sind Fokalkegelschnitte. Da sich umgekehrt aus den Fokalkegelschnitten jede der durch bestimmte Quadrik der konfokalen Schar mit Hilfe eines Fadens geeigneter Länge, analog zur Fadenkonstruktion einer Ellipse, konstruieren lässt, nennt man die Fokalkurven der durch bestimmten Schar konfokaler Quadriken.[4][5][6] (siehe Fadenkonstruktion eines 3-achsigen Ellipsoids.)
Dreifaches Orthogonalsystem
Analog zu der Eigenschaft konfokaler Ellipsen/Hyperbeln gilt:
- Durch jeden Punkt mit geht genau eine Fläche jedes der drei Typen.
- Die drei Quadriken durch schneiden sich dort senkrecht.
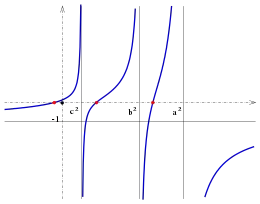
Beweis der Existenz dreier Quadriken durch einen Punkt:
Für einen Punkt mit sei
.
Diese Funktion hat die 3 Polstellen und ist in jedem der offenen Intervalle stetig und streng monoton steigend. Aus dem Verhalten der Funktion in der Nähe der Polstellen und für erkennt man (s. Bild):
Die Funktion hat genau 3 Nullstellen mit
Beweis der Orthogonalität der Flächen:
Mit Hilfe der Funktionenschar
mit dem Scharparameter lassen sich die konfokalen Quadriken durch beschreiben. Für zwei sich schneidende Quadriken mit ergibt sich in einem gemeinsamen Punkt
Für das Skalarprodukt der Gradienten in einem gemeinsamen Punkt folgt daraus

Anwendungen:
Nach einem Satz von Charles Dupin über dreifach orthogonale Flächensysteme gilt (s. Weblinks):
- Je zwei verschiedenartige konfokale Quadriken schneiden sich in Krümmungslinien.
- Analog zu den (ebenen) elliptischen Koordinaten gibt es im Raum Ellipsoid-Koordinaten. Die einfachste Form von Ellipsoid-Koordinaten verwendet die zu einem Punkt gehörigen Parameter der konfokalen Quadriken durch diesen Punkt.[7]
In der Physik spielen konfokale Ellipsoide als Äquipotentialflächen eine Rolle:[8]
- Die Äquipotentialflächen der freien Ladungsverteilung auf einem Ellipsoid sind die dazu konfokalen Ellipsoide.
Satz von Ivory
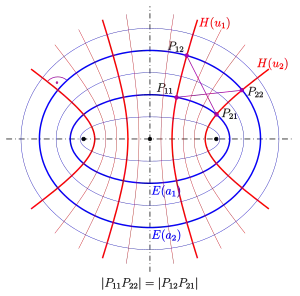
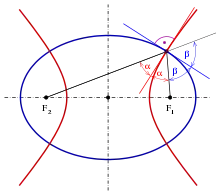
Der Satz des schottischen Mathematikers und Astronomen James Ivory (1765–1842) macht eine Aussage über Diagonalen in einem „Netz-Rechteck“ (einem durch orthogonale Kurven gebildeten 4-Eck):
- In jedem Viereck eines Netzes konfokaler Ellipsen und Hyperbeln, das von zwei Ellipsen und zwei Hyperbeln gebildet wird, sind die Diagonalen gleich lang (s. Bild).
Schnittpunkte einer Ellipse mit einer konfokalen Hyperbel:
sei die Ellipse mit den Brennpunkten und der Gleichung
sei die dazu konfokale Hyperbel mit der Gleichung
Berechnet man die Schnittpunkte von und , so ergeben sich folgende vier Punkte:
Diagonalen in einem Netzviereck:
Um die Rechnung übersichtlich zu halten, wird hier vorausgesetzt, dass
- ist, was keine wesentliche Einschränkung ist, da alle anderen konfokalen Netze durch eine Skalierung (Streckung am Mittelpunkt) erhalten werden können.
- Von den Alternativen (bei den Schnittpunkten) wird nur benutzt. Am Ende überlegt man sich, dass andere Vorzeichnenkombinationen zum selben Resultat führen.
Es seien zwei konfokale Ellipsen und zwei dazu konfokale Hyperbeln gegeben. Es werden die Diagonalen des Netzvierecks bestehend aus den 4 Schnittpunkten
berechnet:
Der letzte Term ist offensichtlich invariant gegenüber der Vertauschung . Genau diese Vertauschung führt zu . Also gilt:
Die Gültigkeit des Satzes von Ivory für konfokale Parabeln lässt sich auch leicht rechnerisch nachweisen.
Ivory hat auch die 3-dimensionale Form des Satzes bewiesen (s. Blaschke, S. 111):
- In einem von konfokalen Quadriken begrenzten „krummflächigen Quader“ sind die 4 Diagonalen gegenüberliegender Punkte gleich lang. Dies gilt auch für jedes Diagonalenpaar der Seitenflächen.
Siehe auch
Einzelnachweise
- A. M. Schoenflies, Max Dehn: Einführung in die Analytische Geometrie der Ebene und des Raumes. Grundlehren der math. Wiss. in Einzeld., Band XXI, Springer, Berlin 1931, S. 135.
- Felix Klein: Vorlesungen über Höhere Geometrie. Springer-Verlag, Berlin 1926, S. 32.
- Felix Klein: Vorlesungen über höhere Geometrie,Springer-Verlag, 2013, ISBN 3642886744, S. 20.
- Staude, O.: Ueber Fadenconstructionen des Ellipsoides. Math. Ann. 20, 147–184 (1882)
- Staude, O.: Ueber neue Focaleigenschaften der Flächen 2. Grades. Math. Ann. 27, 253–271 (1886).
- Staude, O.: Die algebraischen Grundlagen der Focaleigenschaften der Flächen 2. Ordnung Math. Ann. 50, 398 – 428 (1898)
- F. Klein: Vorlesungen über Höhere Geometrie, Springer-Verlag, 2013,ISBN 3642886744, S. 19.
- D. Fuchs, S. Tabachnikov: Ein Schaubild der Mathematik. Springer-Verlag, Berlin/Heidelberg 2011, ISBN 978-3-642-12959-9, S. 480.
Literatur
- W. Blaschke: Analytische Geometrie. Springer, Basel 1954, ISBN 978-3-0348-6813-6, S. 111.
- D. Hilbert, S. Cohn-Vossen: Anschauliche Geometrie. Springer, 1996, ISBN 978-3-642-19947-9.
- Horst Knörrer: Geometrie. Vieweg-Verlag, Wiesbaden 2006, ISBN 978-3-8348-0210-1, S. 198.
- E. Pascal: Repertorium der höheren Mathematik. Teubner, Leipzig/Berlin 1910, S. 257.
- R. Resel: Reise zum Mittelpunkt der Mathematik. Logos-Verlag, Berlin, ISBN 978-3-8325-3672-5, S. 259.
- K. Baer: Parabolische Koordinaten in der Ebene und im Raum. Königliche Hofbuchdruckerei Trowizsch u. Sohn, Frankfurt a. O. 1888.
Weblinks
- T. Hoffmann: Miniskript Differentialgeometrie I. S. 48 ff.
- O. Staude: Die Fokaleigenschaften der Flächen 2. Ordnung, Encyklopädie der mathematischen Wissenschaften mit Einschluss ihrer Anwendungen, 1903, S. 204
- B. Springborn: Kurven und Flächen, 12. Vorlesung: Konfokale Quadriken. S. 22 f.
- H. Walser: Konforme Abbildungen. S. 8.