Konfiguration (Mechanik)

In der Kontinuumsmechanik ist eine Konfiguration die Abbildung eines Körpers aus dem euklidischen Raum unserer Anschauung in einen abstrakten euklidischen Vektorraum. Auf diese Weise wird der physikalische Körper einer mathematischen Beschreibung zugänglich. Er ist die Grundlage für die Kinematik, die Formulierung von Naturgesetzen und Stoffgesetzen.

Dieser Artikel wurde in die Qualitätssicherung der Redaktion Physik eingetragen. Wenn du dich mit dem Thema auskennst, bist du herzlich eingeladen, dich an der Prüfung und möglichen Verbesserung des Artikels zu beteiligen. Der Meinungsaustausch darüber findet derzeit nicht auf der Artikeldiskussionsseite, sondern auf der Qualitätssicherungs-Seite der Physik statt.

Die Konfiguration darf nicht mit dem Körper noch mit seiner Bewegung oder Deformation verwechselt werden; sie soll diese nur zu jeder Zeit getreu abbilden. Ihre Definition beinhaltet jedoch bereits die Kontinuumshypothese (s. u.), der zufolge die Eigenschaften eines realen Körpers kontinuierlich über den Raum verteilt sind.

Körper

Ein Körper unserer Anschauung ist ein abgegrenzter mit Materie gefüllter Raumbereich. Es wurde mehrfach versucht, Körper als Ausschnitt des Universums darzustellen, was aber formal aufwendig ist. Stattdessen soll er nach dem Schnittprinzip für lokale Analysen aus dem Universum herausgeschnitten werden, wobei die Schnittränder recht willkürlich gewählt werden dürfen. Auf diese Weise bekommt der Körper eine Oberfläche, die abschnittsweise glatt sein soll.[1]

Der Körper darf innere Oberflächen also Löcher aufweisen, soll aber zwischen diesen Oberflächen zusammenhängend sein und den Raum gleichmäßig mit Materie füllen. Sind die Eigenschaften der Materie im Körper unter gleichen Bedingungen gleich, dann ist der Körper homogen, ansonsten inhomogen.

Treten dazu unterschiedliche Phasen auf, so spricht man von heterogenen Körpern.

Kontinuumshypothese

Zur Erläuterung der Kontinuumshypothese soll der Körper makroskopisch aus nur einem Material bestehen. Der Körper wird unter Anwendung des Schnittprinzips in Teilkörper zerschnitten. Das Gesamtvolumen $V$ teilt sich dann in die Teilvolumina ${v}_{i}>0$ auf, derart, dass das Gesamtvolumen die Summe der Einzelvolumina ist

V=\sum _{i}v_{i}

.

Jeder der Teilkörper hat eine Masse ${m}_{i}>0$ und analog zum Volumen soll die Gesamtmasse $M$ des Körpers die Summe der Massen der Teilkörper sein:

M=\sum _{i}m_{i}

.

Jedem Teilkörper kann eine mittlere Dichte

\rho _{i}={\frac {m_{i}}{v_{i}}}>0

und weitere physikalische Eigenschaften, z. B. eine Temperatur, zugeordnet werden. Eine Annahme, die sich in vielen praktischen Problemen bewährt hat, ist die, dass sich die Eigenschaften von einem Volumen zum nächsten nur geringfügig ändern, sich also ein stetiger Verlauf der Eigenschaften, z. B. der Dichte, im Körper ergibt. Dies ist die Kontinuumshypothese. Man sagt auch, dass die Eigenschaften über den Körper verschmiert werden. Im Grenzwert $v_{i}\rightarrow 0$ geht die Summe über die Massen der Teilkörper in ein Volumenintegral über:

M=\lim _{n\to \infty  \atop v_{i}\to 0}\sum _{i=1}^{n}\rho _{i}v_{i}=\int _{V}\rho \,\mathrm {d} V

.

Die Berechenbarkeit dieses Integrals setzt voraus, dass auch die materiellen Punkte selbst gleichmäßig über den Raum verteilt sind, d. h. das Volumen eine kompakte Punktmenge ist.

Definition der Konfiguration

Sei ein Körper $K$ eine kompakte, stückweise glatt berandete Menge[1] von Partikeln $P$ und $\mathbb {R} ^{3}$ ein euklidischer Vektorraum. Dann ist jede Abbildung $\kappa$

{\displaystyle {\begin{array}{llll}\kappa

eine Konfiguration.

Um physikalisch Sinn zu machen, muss diese Abbildung

stetig[2] sein, so dass vormals benachbarte Punkte benachbart bleiben,
stetig differenzierbar sein[3], so dass glatte Partien glatt bleiben,
ein-eindeutig umkehrbar[4] sein, so dass der Körper sich nicht selbst durchdringen kann und
die Orientierung erhalten, da Spiegelungen materieller Körper in der Natur nicht möglich sind.

Das Bezugssystem wird so gewählt, dass der Vektor ${\vec {x}}$ dieselben Koordinaten hat wie der Partikel im Raum unserer Anschauung.

Im Sprachgebrauch wird oftmals vereinfachend das Bild ${\vec {x}}$ als Konfiguration und $V$ als Volumen des Körpers bezeichnet.

Spezielle Konfigurationen

Referenzkonfiguration

Die Referenz- oder Bezugskonfiguration[5] ist eine zeitlich fixierte Konfiguration, die der Namensgebung für die materiellen Punkte dient. Der Name eines materiellen Punktes $P$ ist dann der Vektor ${\vec {x}}$ . Die Referenzkonfiguration braucht vom materiellen Körper zu keinem Zeitpunkt(!) eingenommen zu werden.

Für einen beliebig geformten viereckigen Körper eignet sich z. B. das Einheitsquadrat als Referenzkonfiguration.

Ausgangskonfiguration

Die Ausgangskonfiguration $\kappa (t_{0})$ bezeichnet den Ausgangszustand des materiellen Körpers zu einem festgelegten Zeitpunkt $t_{0}$ . Weil dieser Zustand einmal eingenommen wurde, beschreibt diese Konfiguration ein Objekt unserer Anschauung. Im Maschinenbau wird dazu meist die Konstruktionslage verwendet; auf Umformprozessen aufbauende Analysen können aber auch den umgeformten Zustand des Bauteils benutzen.

Auch die Ausgangskonfiguration kann als Referenzkonfiguration dienen und wird dann auch als solche bezeichnet.

Momentankonfiguration

Die Bewegung eines materiellen Körpers wird von einer stetigen Folge zeitabhängiger Konfigurationen $\kappa \left(t\right),t\geq t_{0}$ beschrieben. Die zeitabhängige Konfiguration $\kappa \left(t\right)$ wird Momentankonfiguration genannt.

Zwischenkonfiguration

In der große Deformationen behandelnden Materialtheorie werden Zwischenkonfigurationen eingeführt, um auf ihnen Materialmodelle zu formulieren. Diese Zwischenkonfigurationen werden durch eine lokale Entlastung erreicht, was man sich so vorstellen kann, dass ein Volumenelement des Körpers freigeschnitten und entlastet wird, wodurch es aber seine Form ändert. Nach der Entlastung werden benachbarte Volumenelemente im euklidischen Raum nicht mehr zusammen passen. Man sagt auch, dass die Verzerrungen inkompatibel sind, was bedeutet, dass es kein Bewegungsfeld gibt, aus dem sich die Verzerrungen ableiten lassen.

Repräsentatives-Volumen-Element

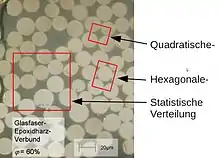
Mögliche RVE bei faserverstärktem Kunststoff

Liegt ein inhomogenes Material vor, z. B. faserverstärkter Kunststoff, so kann die beschriebene Homogenisierung schwierig sein. Schließlich will man ein inhomogenes Material mit homogen verteilten Eigenschaften modellieren, um es einer effizienten Analyse zugänglich zu machen.

Der pragmatische Ansatz ist der, das kleinste Volumen zu wählen, das (vermutlich) bei einer Messung seiner Eigenschaften einen dem ganzen Körper vergleichbaren Wert liefert. Dieses kleinste Volumen nennt man repräsentatives Volumenelement (RVE), und man stellt sich vor, dass der ganze Körper aus Kopien dieses RVE aufgebaut ist.

Für die Wahl des RVE gibt es oftmals verschiedene Möglichkeiten – wie das Bild zeigt, und welches die beste Wahl ist, misst sich daran, wie gut das Modell das makroskopische Materialverhalten widerspiegelt und ob dies mit vertretbarem Aufwand möglich ist.

Siehe auch

Literatur

H. Giesekus: Phänomenologische Rheologie: eine Einführung. Springer, Berlin 1994, ISBN 3-540-57513-8, books.google.de/books?isbn=3540575138
K. Willner: Kontinuums- und Kontaktmechanik: synthetische und analytische Darstellung. Springer, Berlin 2003, ISBN 3-540-43529-8, books.google.de/books?isbn=3540435298
H. Altenbach: Kontinuumsmechanik: Einführung in die materialunabhängigen und materialabhängigen Gleichungen. 2. Aufl., Springer Vieweg, Berlin 2012, ISBN 978-3-642-24118-5
H. Bertram: Axiomatische Einführung in die Kontinuumsmechanik. Bibliographisches Institut Wissenschaftsverlag, Mannheim 1989, ISBN 3-411-14031-3.
P. Haupt: Continuum Mechanics and Theory of Materials. 2. Aufl., Springer, Berlin 2002, ISBN 978-3-540-43111-4

Einzelnachweise

A. Bertram, S. 67. Die Glattheit wird gebraucht, damit der Divergenzsatz gilt
H. Giesekus, S. 10
A. Bertram, S. 70
H. Giesekus, S. 10, Gl. 2.1
K. Willner, S. 56

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[divergenz-1] A. Bertram, S. 67. Die Glattheit wird gebraucht, damit der Divergenzsatz gilt

[2] H. Giesekus, S. 10

[3] A. Bertram, S. 70

[4] H. Giesekus, S. 10, Gl. 2.1

[5] K. Willner, S. 56