Knotenlinie

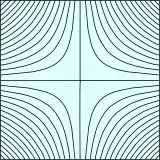
Knotenlinie (englisch Nodal line)[1] heißt eine Linie, die die Punkte einer Funktion $f(x,y)$ zweier Variabler $(x,y)$ verbindet, an denen der Funktionswert verschwindet, in üblicher Formelschreibweise $f(x,y)=0$ . Knotenlinien sind von Bedeutung bei der Untersuchung der Lösungen (kontinuierlicher) Eigenwertprobleme der mathematischen Physik, insbesondere in der Akustik bei (stehenden) Wellen, bei Schwingungen von Scheiben, Platten und Membranen. Für ein tiefes Studium der Natur der Eigenfunktionen ist die Betrachtung der Knotenlinien und ihrer Eigenschaften von der größten Bedeutung.[2] Bekannt geworden sind sie in der Experimentalphysik durch die Chladnischen Klangfiguren. Gezeichnete Knotenlinien wurden erstmals von Chladni im Jahr 1787 veröffentlicht,[3] der auch den naheliegenden Namen Knotenlinien prägte.[4] Die erste Grafik[5] zeigt Knotenlinien in bekannter Art, wie sie auch Chladni gezeichnet hat. Knotenlinien sind das zweidimensionale Analogon zu Knotenpunkten im eindimensionalen und Knotenflächen im dreidimensionalen Fall.

Knotenlinien unterschiedlicher Eigenschwingungen (Moden) einer homogenen quadratischen Scheibe nach Chladni

Einführung

Knotenlinien sinusartiger 2D-Funktionen

Funktion

f(x,y)=\sin(x\cdot y)

Funktion

f(x,y)=\sin(x)\cdot sin(y)

Knotenlinien treten dann auf, wenn die Funktion $f(x,y)$ im untersuchten Wertebereich der unabhängigen Variablen $(x,y)$ sowohl positive als auch negative Werte annimmt. Als dafür typische Funktionen gelten die Winkelfunktionen. Das System der Knotenlinien bilden alle Punkte, die die Bedingung $f(x,y)=0$ erfüllen. Knotenlinien besitzen alle 2D-Funktionen, die um den Nullwert „schwanken“. Wenn man sich die Funktionswerte bildlich als „Landschaft“ vorstellt, dann markieren die Knotenlinien die „Küstenumrisse“. Sie bilden spezielle Höhenlinien, und zwar die mit einer Höhe Null. Das sei an zwei Grafiken veranschaulicht. Für beide Grafiken wurde der Ursprung des Koordinatensystems in die Mitte der jeweiligen Grafik gelegt, die Koordinatenachsen sind in üblicher Lage angeordnet.

In der linken Grafik sind die Knotenlinien der einfachen Funktion $f(x,y)=\sin(x\cdot y)$ dargestellt, und zwar im Wertebereich der unabhängigen Variablen $-4\ {\sqrt {\pi }}\leq x,y\leq 4{\sqrt {\pi }}$ . Die Knotenlinien bilden die Punkte, die die Bedingung $\sin(x\cdot y)=0$ erfüllen. Zwei der Knotenlinien dieser Funktion sind die beiden Koordinatenachsen, sind folglich Geraden, die anderen sind hyperbelartig.

Für die Funktion $f(x,y)=\sin(x)\cdot \sin(y)$ , dargestellt im Wertebereich $-4\ \pi \leq x,y\leq 4\ \pi$ , sind z. B. die Koordinatenachsen ebenfalls Knotenlinien, da sie die Bedingung $\sin(0)\cdot \sin(y)=\sin(x)\cdot \sin(0)=0$ erfüllen. Alle Knotenlinien dieser Funktion bilden ein quadratisches Gitter mit einer Gitterschrittweite von $\Delta x=\Delta y=\pi$ . Die Flächen gleichen Vorzeichens sind Quadrate und bilden ein Schachbrettmuster. Obwohl die Knotenlinien dieses Gitters recht trivial erscheinen, gehören sie dennoch zu dem Funktionstyp, auf den vielgestaltige Eigenfunktionen des (kontinuierlichen) Eigenwertproblems in zwei Dimensionen bei quadratischen, rechteckigen und dreieckigen Scheiben, Platten oder Membranen zurückgehen.

Darstellungen einer Funktion zweier Variabler

Zwei Darstellungen ein und derselben Funktion

3D-Darstellung einer Funktion zweier Variabler. Funktionswerte größer als Null, sind grün, Funktionswerte Null oder kleiner als Null sind blau eingefärbt. Gezeichnet mit der Tabellenkalkulation Microsoft Excel

Flächen gleichen Vorzeichens. Knotenlinien sind die Farbgrenzen und die äußeren Ränder

Eine Funktion zweier Variabler $f(x,y)$ kann man darstellen, indem man sie zunächst in ein dreidimensionales (kartesisches oder polares) Koordinatensystem zeichnet. Über der Ebene $(x,y)$ wird der Funktionswert in Richtung der $z$ -Achse eingetragen. So ergibt sich als Bild typischerweise eine „Landschaft“ mit „Gebirgen“ und „Meerestiefen“. Dieses 3D-Bild wiederum kann man in die Ebene der Zeichnung bei unterschiedlicher Beleuchtung von verschiedenen Entfernungen und Blickwinkeln aus projizieren. Dieser Typ 3D-Darstellung ist verbreitet und im ursprünglichen Wortsinn „anschaulich“. Obwohl eine solche 3D-Darstellung eindrucksvoll sein kann, sind manche wichtigen Details schwer auszumachen, zum Beispiel: Wo sind denn nun die Grenzen von „Land“ und „Meer“, wo ist die Funktion größer und wo ist sie kleiner als Null?

Das zeigt die schlichte rechte Grafik vom Typ Flächen gleichen Vorzeichens besser: In den grünen Flächen ist die Funktion größer, in den blauen kleiner als Null. Die Grenzen zwischen Grün und Blau und die äußeren Ränder bilden die Knotenlinien. Eine der Knotenlinien dieser speziellen Funktion ist eine Gerade, die von einer Ecke zur gegenüberliegenden verläuft. Es liegt deshalb nahe, die 3D-Grafik so zu drehen, dass man einen „freien Blick“ durch das „Tal“ dieser Knotenlinie hat.

Wenn man sich auf die Darstellung der Knotenlinien einer Funktion allein beschränkt, sie etwa wie üblich als schwarze Linie zeichnet, kann man schnell einen optischen Eindruck über ihre Eigenschaft Nullstellen gewinnen. Drehungen, Projektionen und Beleuchtungen, die bei einer 3D-Darstellung festgelegt werden müssen, entfallen. Man schließt aus der Grafik, dass in der von Knotenlinien umschlossenen Fläche der Funktionswert entweder größer oder kleiner als Null ist.

Dargestellt ist die Funktion

u(x,y)=\sin(\pi \ {\frac {x}{a}})\cdot \sin(4\ \pi \ {\frac {y}{a}})-\sin(4\ \pi \ {\frac {x}{a}})\cdot \sin(\pi \ {\frac {y}{a}})

,

im Inneren und auf dem Rand des Quadrats mit der Seitenlänge $a$ . Zum Ursprung des Koordinatensystems nur soviel: Er liegt in einer Ecke des Quadrats, nicht in der Mitte wie bei den einführenden Beispielen.

Diese hier zur Illustration gewählte Funktion ist eine spezielle Eigenfunktion, eine Lösung eines vielfach in der Physik auftretenden Problems, eines (kontinuierlichen) Eigenwertproblems. Diese Funktion gehorcht der Nebenbedingung, dass sie auf dem Rand Null wird. Dass das so ist, erkennt man bei der 3D-Darstellung auch optisch. In der Darstellung Flächen gleichen Vorzeichens erkennt man das optisch nicht, sondern man muss hinzufügen: Alle äußeren Ränder sind Knotenlinien.

Um eine solche Grafik, gleich welchen Typs, zeichnen zu können, muss man die Formel der Funktion kennen und die Funktionswerte für hinreichend viele Punkte berechnen und in die Grafik eintragen, was mit einem Computerprogramm heutzutage kein Problem mehr darstellt. Für den Physiker Friedrich Pockels, der im Jahr 1891 (genaue) Knotenlinien-Grafiken von Hand erstellt hat, aber schon.[6] Kennt man z. B. die eine Differentialgleichung lösende Funktion nicht, müsste man die Funktionswerte zuerst numerisch berechnen, z. B. mit der Finite-Differenzen-Methode.

Knotenlinien in der Akustik

Trommelfell, das in der Grundmode schwingt und nur eine Knotenlinie besitzt, die auf dem äußeren Rand liegt

Knotenlinien (Chladni-Moden) einer Gitarrendecke mit den zugehörigen Frequenzen

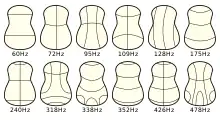
In der Akustik sucht man spezielle Funktionen, die Eigenfunktionen, auch Moden genannt, und die zu jeder Mode gehörende Frequenz der Instrumente. Solche Eigenfunktionen werden (auch) im 2D-Fall aus einer partiellen Differentialgleichung (s. u.) berechnet, wobei Materialeigenschaften, Geometrie und Randbedingungen in die Rechnung eingehen. Wir beschränken uns hier nur auf den ortsabhängigen Teil der Lösung einer orts- und zeitabhängigen Gleichung, die die Schallerzeugung der Instrumente beschreibt. Um die Knotenlinien herum schwingen die Resonanzkörper. Es werden beim Musizieren viele Moden angeregt, die sich additiv überlagern.

Bei zweidimensionalen (ebenen) akustischen Schallerzeugern hängt die Lage der Knotenlinien u. a. von der geometrischen Gestalt des schwingenden Körpers, aber auch entscheidend von den Randbedingungen ab. Bei der Membran einer Trommel z. B. kann die Randbedingung als Null angenommen werden, weil sie am Rand eingespannt ist. Jedes Instrument hat einen Grundton, eine Grundmode. Wenn dieser im Fall der Trommel ertönt, schwingt das Fell so, dass die einzige Knotenlinie auf der Randkontur liegt, wie es die Animation zeigt. Er wir durch Schlagen auf das Zentrum angeregt. Treten im Inneren der Membran Knotenlinien auf, bedeutet das, dass ein Oberton angeregt worden ist, dessen Frequenz, wie der Name sagt, höher ist als die des Grundtons.

Bei einem idealisierten Becken, einer ebenen, homogenen, kreisförmigen Scheibe aus Messing, kann der Außenrand frei schwingen. Es wird daher angenommen werden, dass die Normalenableitung an den Orten des äußeren Randes verschwindet. Zum Grundton eines solchen Instruments gehört keine Knotenlinie, sondern nur ein Knotenpunkt in der Mitte. Die Eigenfunktionen (und zugehörigen Frequenzen) lassen sich für beide Fälle (Trommel oder Becken) analytisch berechnen. wobei bei kreisförmigen Objekten Besselfunktionen an die Stelle treten, die bei Recht- oder Dreiecken die elementaren trigonometrischen Funktionen einnehmen.

Bei anders gestalteten Instrumenten, wie z. B. für Gitarren und andere Zupf- oder für Streichinstrumente, besonders aber für Glocken, ist es deutlich schwieriger, die Frequenzen ihrer Obertöne zu berechnen und die Lage entsprechender Knotenlinien zu finden. Ist der Instrumentenkörper gewölbt, versagt auch das Chladni-Experiment.

Unterschied zwischen Knotenlinien und Chladnische Klangfigur

Knotenlinien und simulierte Chladnische Klangfigur einer speziellen Eigenfunktion der quadratischen, freischwingenden Platte

Knotenlinien

Chladnische Klangfigur

Nicht selten werden Knotenlinien und Chladnische Klangfiguren synonym verwendet. Das ist nicht korrekt. Knotenlinien sind mathematisch streng definiert und für viele Zweige der Physik relevant, nicht nur für die Akustik.[7] Eine Knotenlinie ist ein spezielles abstraktes Objekt, eine Chladnische Klangfigur dagegen ein reales Muster, das auf einer mit Sand bestreuten dünnen Platte entsteht, wenn diese in Schwingungen versetzt wird.

Die linke Grafik zeigt die Knotenlinien einer speziellen Eigenfunktion (Mode). Es handelt sich um eine Eigenfunktion einer quadratischen Platte mit freien Enden (die Normalenableitung an den Rändern ist Null). Auf der einführenden Grafik des Artikels ist diese Mode links unten eingezeichnet. Die rechte Grafik ist eine Simulation der entsprechenden Chladnischen Klangfigur, zeigt also jene Stellen, wo sich der Sand sammelt. An manchen Stellen sehen wir Verdickungen, und zwar an den Orten, wo die Amplitude der Schwingungen gering ist.

Es handelt sich bei der Grafik um die Knotenlinien der Eigenfunktion $u(x,y)$ mit der Formel

u(x,y)=\cos(2\ \pi \ {\frac {x}{a}})\cdot \cos(4\ \pi \ {\frac {y}{a}})-\cos(4\ \pi \ {\frac {x}{a}})\cdot \cos(2\ \pi \ {\frac {y}{a}})

,

wobei $a$ die Seitenlänge des Quadrats symbolisiert und der Ursprung des Koordinatensystems in der linken unteren Ecke des Quadrats liegt. Diese Funktion erfüllt die Differentialgleichung und die Randbedingungen, die im nächsten Abschnitt explizit notiert sind.

Wenn Physiker oder Mathematiker auf öffentlichen Veranstaltungen für ihre Berufszweige, insbesondere vor Schülern, werben, werden nicht selten Chladnische Klangfiguren gezeigt. Die brasilianische Webseite Matemateca zeichnet u. a. solche Experimente auf Video auf und veröffentlicht sie, auch in den Wikimedia Commons.[8] Die Mode, die gerade angeregt wird, hängt von der Stelle am Rand ab, wo der Geigenbogenstrich geführt wird. Man kann die Platte auch durch akustische Anregung mittels eines Lautsprechers zum Vibrieren bringen. Wenn die gewählte Anregungsfrequenz einer bestimmten Eigenfrequenz der Platte entspricht, wird die zu dieser Frequenz gehörende Knotenlinie durch den Sand sichtbar.

Es sei angemerkt, dass die so erzeugten Chladnischen Klangfiguren nicht alle Moden einer freischwingenden Platte anregen können. Das ist konstruktionsbedingt, denn die Platte wird (meist) in der Mitte fixiert. Folglich existiert die zusätzliche Bedingung, dass die Mode an dieser Stelle Null sein muss, was nicht alle Moden erfüllen.

Zur Theorie

Der Zweig der mathematischen Physik, in dem Knotenlinien zur Visualisierung von 2D-Funktionen nützlich sein können, ist der, bei dem man ein (kontinuierliches) gewöhnliches oder verallgemeinertes Eigenwertproblem in zwei Dimensionen zu lösen hat. Vor dieser Aufgabe steht man zum Beispiel bei der Lösung der partiellen Differentialgleichung der freien Schwingung der Akustik, bei der Lösung der stationären Schrödingergleichung der Quantenmechanik, somit in Atomphysik, theoretischer Chemie und Kernphysik, und in der Reaktorphysik, wo man die zeitunabhängige Neutronen-Diffusionsgleichung zu lösen hat.

Es würde hier den Rahmen sprengen, die Theorie detailliert darzustellen, die bereits im 19. Jahrhundert ausgearbeitet wurde. Wer sich für die Grundlagen, angewendet auf den Fall von Knotenlinien rechteckiger Scheiben, Platten und Membranen, interessiert, dem sie die Monographie von Friedrich Pockels von 1892 empfohlen.[9]

Die Aufgabe in allen genannten Fachrichtungen, sofern es ein 2D-Problem ist, besteht darin, die folgende lineare homogene elliptische partielle Differentialgleichung zu lösen:

{\frac {\partial ^{2}u(x,y)}{\partial x^{2}}}+{\frac {\partial ^{2}u(x,y)}{\partial y^{2}}}+k^{2}\cdot u(x,y)=0

,

mit den Eigenwerten $k^{2}$ und den gesuchten Eigenfunktionen[10]

h\cdot {\overline {u}}+{\frac {\partial {\overline {u}}}{\partial n}}=0

erfüllen. Der Term ${\overline {u}}$ symbolisiert die vorgegebenen Funktionswerte auf dem Rand, der Faktor $h$ , ebenfalls vorgegeben, ist auf dem gesamten Rand konstant. Der Term $\textstyle {\frac {\partial {\overline {u}}}{\partial n}}$ symbolisiert die vorgegebene Normalenableitung auf dem Rand. Oft sind, wie oben angesprochen, zwei Spezialfälle von Interesse: Entweder sei der Funktionswert auf dem Rand Null ( ${\overline {u}}=0$ ) oder die Normalenableitung sei Null ( $\textstyle {\frac {\partial {\overline {u}}}{\partial n}}=0$ ).

Für einige Spezialfälle sind analytische Lösungen dieser Gleichung bekannt, auf die bei der Zeichnung einiger der obigen Grafiken zurückgegriffen wurde.

Literatur

Ernst Florens Friedrich Chladni: Entdeckungen über die Theorie des Klanges. Weidmanns Erben und Reich, Leipzig 1787 (77 S., online).

Ernst Florens Friedrich Chladni: Die Akustik: Mit 12 Kupfertafeln. Breitkopf & Härtel, Leipzig 1802 (XXXII, 310, online).
John William Strutt Rayleigh: The theory of sound, Volume I. Macmillan and Co., London 1877 (326 S., online).

John William Strutt Rayleigh: Die Theorie des Schalles, Erster Band. Autorisirte deutsche Ausgabe Auflage. Druck und Verlag von Friedrich Vieweg und Sohn, Braunschweig 1879 (XVI, 427 S., online).

Friedrich Pockels, Felix Klein: Über die partielle Differentialgleichung $\Delta u+k^{2}u=0$ und deren Auftreten in der mathematischen Physik: Mit Figuren im Text. Druck und Verlag von B. G. Teubner, Leipzig 1891 (339 S., online).

Richard Courant, David Hilbert: Methoden der mathematischen Physik I (Die Grundlehren der mathematischen Wissenschaften in Einzeldarstellungen. Band XII). Julius Springer, Berlin 1924 (450 S., online).

Einzelnachweise und Anmerkungen

John Rayleigh 1877, S. 252
Richard Courant, 1924, S. 248
Chladni 1787
Chladni 1802, S. 117
Für die grafische Darstellung einer Funktion hat sich (außer in der mathematischen Physik) der Begriff Funktionsgraph eingebürgert. Für die hier dargestellten Grafiken trifft jedoch der Begriff Grafik der Funktion den Sachverhalt besser, da ja nicht die Funktion („als Ganzes“) dargestellt wird, sondern nur ihre Knotenlinien.
Friedrich Pockels, 1891, S. 80
In der Mathematik wird der Begriff Knotenlinie eher selten verwendet.
matemateca IMEUSP. Abgerufen am 20. Februar 2022.
Friedrich Pockels, 1892, ab S. 76
Es sind in der Regel unendlich viele, von denen meist nur einige wenige berechnet werden. In der Reaktorphysik zum Beispiel ist die gesuchte Eigenfunktion die physikalische Größe Neutronenfluss, die per definitionem nur positiv oder Null sein kann. Das erfüllt aber nur die Grundmode (englisch Fundamental mode). Folglich wird nur diese eine Mode berechnet.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] John Rayleigh 1877, S. 252

[2] Richard Courant, 1924, S. 248

[3] Chladni 1787

[4] Chladni 1802, S. 117

[5] Für die grafische Darstellung einer Funktion hat sich (außer in der mathematischen Physik) der Begriff Funktionsgraph eingebürgert. Für die hier dargestellten Grafiken trifft jedoch der Begriff Grafik der Funktion den Sachverhalt besser, da ja nicht die Funktion („als Ganzes“) dargestellt wird, sondern nur ihre Knotenlinien.

[6] Friedrich Pockels, 1891, S. 80

[7] In der Mathematik wird der Begriff Knotenlinie eher selten verwendet.

[8] matemateca IMEUSP. Abgerufen am 20. Februar 2022.

[9] Friedrich Pockels, 1892, ab S. 76

[10] Es sind in der Regel unendlich viele, von denen meist nur einige wenige berechnet werden. In der Reaktorphysik zum Beispiel ist die gesuchte Eigenfunktion die physikalische Größe Neutronenfluss, die per definitionem nur positiv oder Null sein kann. Das erfüllt aber nur die Grundmode (englisch Fundamental mode). Folglich wird nur diese eine Mode berechnet.