Fabry-Pérot-Interferometer
Das Fabry-Pérot-Interferometer, auch Pérot-Fabry-Interferometer, wurde 1897 von den französischen Physikern Charles Fabry und Alfred Pérot entwickelt. Es ist ein optischer Resonator, der aus zwei teildurchlässigen Spiegeln gebildet wird. Ist der Spiegelabstand unveränderbar (bspw. Glas mit aufgedampften Spiegeln), so werden diese Aufbauten auch als Maßverkörperung benutzt und dann als Fabry-Pérot-Etalon bezeichnet. Ein eintreffender Lichtstrahl wird nur dann durch diesen Aufbau geleitet (transmittiert), wenn er dessen Resonanzbedingung erfüllt.
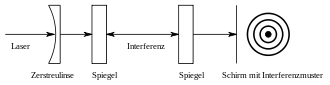

Damit lässt sich das Fabry-Pérot-Interferometer u. a. als optischer Filter einsetzen, der aus einer breitbandigen Strahlung ein schmalbandiges Spektrum herausfiltert. Spiegelverschiebungen ermöglichen es darüber hinaus, die spektralen Eigenschaften der transmittierten Strahlung einzustellen. Das Transmissionsverhalten lässt sich mit der Airy-Formel berechnen.
Wirkungsweise
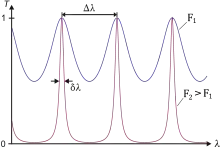
Das Fabry-Pérot-Interferometer besteht aus zwei teilreflektierenden Spiegeln hoher Reflektivität, die miteinander einen optischen Resonator bilden. Das Transmissionsspektrum dieser Anordnung zeigt schmale Transmissions-Maxima für Wellenlängen, welche die Resonanzbedingung erfüllen, während andere Spektralbereiche in der Transmission nahezu vollständig ausgelöscht werden. Dies geschieht durch konstruktive bzw. destruktive Interferenz der Teilstrahlen.
Der Abstand der Transmissionsmaxima heißt freier Spektralbereich (FSB) des Resonators. Der Frequenzabstand ist vom Spiegelabstand und dem Brechungsindex des Materials zwischen den Spiegeln abhängig:
Die Finesse dient zur Charakterisierung des Resonators. Sie ist definiert als Verhältnis zwischen dem freien Spektralbereich und der Halbwertsbreite eines einzelnen Maximums:
- .
Ein alternatives Maß ist der Finesse-Koeffizient , der durch
definiert ist.
Je größer die Finesse, desto mehr Strahlenbündel interferieren miteinander und desto schärfer sind also die Interferenzringe. Einfachste Fabry-Pérot-Interferometer erreichen bei sichtbarem Licht Finessen von ungefähr . Bei hohen Reflektivitäten der Spiegel und geringer Dämpfung im Resonator nimmt die Finesse große Werte an:
Mit dielektrischen Dünnschichtbelägen und gekrümmten Spiegeln lassen sich Finessen bis zu erreichen.[1]
Bei steigender Finesse wächst bei Resonanz die Intensität bzw. Feldstärke der Lichtwellen innerhalb des Interferometers bzw. Resonators auf Werte an, die wesentlich höher sind als diejenigen des durchtretenden Lichtes. Diese Tatsache muss bei Anwendungen, bei denen die Leistung im Vordergrund steht, berücksichtigt werden (z. B. bei Laser-Resonatoren und -Modulatoren).
Die transmittierte Intensität berechnet sich zu
- .
Mit der Phasendifferenz (siehe Durchmesser der Interferenzringe unten)
ergibt sich weiter
- .
Die Resonanzmaxima sind die longitudinalen Moden eines Lasers. Je nach dessen Verstärkungsbandbreite kann er auf einer oder auf mehreren dieser Moden anschwingen bzw. „lasern“.
Durchmesser der Interferenzringe
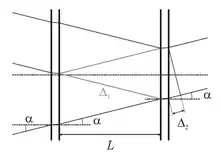
Der Wegunterschied und die Phasendifferenz sind nach der Skizze gegeben durch
- ,
mit der Phasendifferenz
- .
Mit der Interferenzordnung folgt
und aufgelöst nach
- .
Daraus folgen Resonanzwellenlänge und Resonanzfrequenz der Ordnung :
und
- .
Zu jedem Interferenzring gehört also ein Winkel , wie sich dieser für verschiedene Interferenzordnungen ändert, wird später klarer. Zunächst gilt es noch den freien Spektralbereich als Funktion des Einfallswinkels auszudrücken. Dieser ergibt sich aus:
und führt zu:
Um den Abstand der Interferenzringe besser zu veranschaulichen genügt eine Taylor-Entwicklung von:
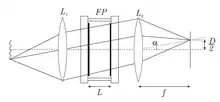
Mit einer Kleinwinkelnäherung ergibt sich für den Ringdurchmesser :
Setzt man nun in die Formel für ein erhält man:
Gleichzeitig ergibt sich für die Resonanzwellenlänge und Resonanzfrequenz:
und
Löst man nach auf, ergibt sich für den Durchmesser der Interferenzringe folgender wurzelförmiger Zusammenhang:

Dabei ist die Interferenzordnung gegeben durch:
ist die Modenzahl im Resonator für und ist nicht zwangsläufig eine natürliche Zahl, weswegen ein Korrekturfaktor eingeführt wird. Die Zahl ist die Nummer des Interferenzringes und wird von innen nach außen gezählt. Nun ist es so, dass für moderate Winkel ungefähr der Resonanzwellenlänge für entspricht, woraus für den Durchmesser des p-ten Ringes folgendes gilt:
Für die Resonanzwellenlänge und die Resonanzfrequenz des p-ten Ringes gilt:
Somit lässt sich zu jedem Ringdurchmesser eine Wellenlänge und eine Frequenz bestimmen, bzw. die Durchmesser der entstehenden Ringe in guter Näherung berechnen.
Anwendungen
Das Fabry-Pérot-Interferometer wird angewendet:
- in der Spektroskopie als durchstimmbarer Interferenzfilter oder auch zur Kalibrierung einer unbekannten oder nichtlinearen Frequenzskala.
- in modifizierter Form in der Forschung als Virtually Imaged Phased Array für spektrometrische Anwendungen oder in der Nachrichtentechnik zum Wellenlängenmultiplexen
- als mechanischer Modulator für monochromatische Strahlung, beispielsweise eines CO2-Lasers bei einer Wellenlänge von 10,6 µm (modulierbare Strahlleistung bis über 100 Watt)
- als Laser-Resonator
- in der Astronomie: im H-alpha-Teleskop zur Sonnenbeobachtung
- als Gravitationswellendetektor, s. KAGRA
Literatur
- Werner Lauterborn, Thomas Kurz: Coherent Optics – Fundamentals and Applications. Springer, 2002, ISBN 3-540-43933-1.
- Wolfgang Zinth, Ursula Zinth: Optik – Lichtstrahlen, Wellen, Photonen. de Gruyter Studium, 2018, ISBN 978-3-11-049501-0.
Einzelnachweise
- M. G. Tarallo, N. Poli, M. Schioppo, D. Sutyrin, G. M. Tino: A high-stability semiconductor laser system for a 88Sr-based optical lattice clock. In: Applied Physics B. Band 103, Nr. 1, 2011, S. 17–25, doi:10.1007/s00340-010-4232-2.