Hohe Harmonische
Hohe Harmonische sind ein Phänomen der Hochintensitätslaserphysik oder der Atomphysik in starken elektromagnetischen Feldern. Durch Fokussieren eines intensiven Femtosekundenlaserpulses in – zumeist – einem Gas unter Vakuum werden zahlreiche höhere Harmonische der Laserfrequenz beobachtet. Dieses Licht mit ungeraden Vielfachen (dreifach, fünffach, siebenfach usw.) der ursprünglichen Laserfrequenz reicht üblicherweise bis ins Ultraviolette oder den weichen Röntgenbereich. Charakteristisch ist, dass eine Vielzahl dieser harmonischen Ordnungen mit ähnlicher Intensität erzeugt wird, bevor die Effizienz des Prozesses abnimmt.
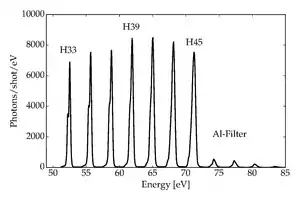
Hohe Harmonische stellen für den Bereich unterhalb 100 nm Wellenlänge eine einfache Methode dar, kohärentes Licht zu erzeugen.
Der Prozess, welcher der Erzeugung der hohen Harmonischen zugrunde liegt, wird ebenfalls angewendet, um Attosekunden-Laserpulse zu erzeugen.[1]
Erzeugung
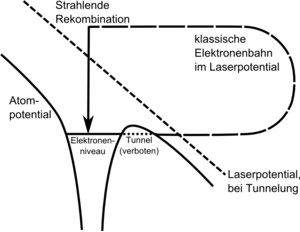
Die Erzeugung hoher Harmonischer erfolgt nach dem „Drei-Schritt-Modell“ (siehe Grafik):
- Durch Bündelung eines Laserpulses mit einer Dauer von 50 fs und kürzer sowie einer Pulsenergie von wenigen mJ (kürzere Pulse erfordern weniger Energie) werden Lichtintensitäten von ca. 1014 W/cm2 erreicht. Bei diesen Intensitäten erreicht das elektrische Feld des Lichts die Stärke des elektrischen Felds im einzelnen Atom. Dies wird durch das Laserfeld so gestört, dass Elektronen eine endliche Chance haben, aus dem Atom ins Kontinuum zu tunneln (das Laserlicht „verbiegt“ das Atompotential).
- Im Kontinuum werden die Elektronen im Vektorpotential des Laserfelds zunächst vom Atomkern wegbeschleunigt, bis sie – aufgrund des wechselnden Vorzeichens – wieder zum Kern zurückkehren.
- Bei der Rückkehr zum Atomkern besteht für das Elektron eine endliche Wahrscheinlichkeit, strahlend mit dem Atom zu rekombinieren, dabei wird die Bewegungsenergie des Elektrons (mehrere Elektronenvolt) als Licht ausgesandt.[2]
Da dieser Prozess nach jedem Maximum des Laserfelds eines Laserpulses längerer Dauer passieren kann und zwei dieser Maxima je Laserzyklus auftreten, kann man aus der Fouriertransformation der Emission schließen, dass ungerade Vielfache der Laserfrequenz erzeugt werden, wohingegen die geraden Vielfachen aus Symmetriegründen wegfallen.
Seit der Verfügbarkeit von Laserpulsdauern im Bereich weniger Femtosekunden und damit Laserzyklen[3] kann die Erzeugung Hoher Harmonischer so beherrscht werden, dass nur zu einem einzigen Zeitpunkt (im Verlauf des Laserpulses) Rekombination möglich ist. Dies führt zur Emission eines UV/XUV-Kontinuums, die diskreten Ordnungen verschwinden.
Anwendungen
Hohe Harmonische ermöglichen die Erzeugung von Laserlicht in bisher nahezu unmöglichen Spektralbereichen, mit einer spektralen Bandbreite, die die Erzeugung von Lichtpulsen ermöglicht, deren Dauer im Attosekundenbereich liegt. Diese Lichtpulse ermöglichen zeitaufgelöste Experimente zur Dynamik der Elektronen im Atom.[4][5] In letzter Konsequenz sind die Attosekundenpulse die Fortführung der Ultrakurzzeitphysik, die mit der Verfügbarkeit von Femtosekundenpulsen begann.
Des Weiteren werden Hohe Harmonische zur Röntgenholographie und zum „Seeding“ von Freie-Elektronen-Lasern benutzt.
Frühere Anwendungen schließen u. a. die Radiographie und Spektroskopie verschiedener Objekte ein.
Literatur
- Hentschel, M., et al. "Attosecond metrology." Nature 414.6863 (2001): 509–513.
- M. Lewenstein, Ph. Balcou, M. Yu. Ivanov, Anne L'Huillier and P. B. Corkum, Theory of high-harmonic generation by low frequency laser fields, Phys. Rev. A 49, 2117, 1994
- T. Brabec & F. Krausz: Intense few-cycle laser fields: Frontiers of nonlinear optics. Rev. Mod. Phys. 72 (No. 2, April 2000), 545–591
- P. M. Paul, E. S. Toma, P. Breger, G. Mullot, F. Auge, Ph. Balcou, H. G. Muller, P. Agostini: Observation of a Train of Attosecond Pulses from High Harmonic Generation. Science 292(5522):1689–1692, 2001.
- M. Hentschel, R. Kienberger, Ch. Spielmann, G. A. Reider, N. Milosevic, T. Brabec, P. Corkum, U. Heinzmann, M. Drescher and F. Krausz: Attosecond metrology. Nature 414 (2001) 509–513